- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на темуРешение неравенств с одной переменной и их систем(8 класс)
Содержание
- 1. Презентация по математике на темуРешение неравенств с одной переменной и их систем(8 класс)
- 2. Математика учит преодолевать трудности и исправлять собственные ошибки. (Декарт).
- 3. Цель урока: Закрепить знания по теме: «Решение неравенств с одним неизвестным и их систем»
- 4. Задачи урока: Повторить и обобщить знания учащихся
- 5. Линейные неравенстваОпределения:Запись вида а>в; а≥в или ав, а
- 6. Что мы должны знать и уметь при решении линейных неравенств
- 7. Линейные неравенстваПравила:1) Любой член неравенства можно переносить
- 8. Линейные неравенстваПравила:2) Обе части неравенства можно умножить
- 9. Линейные неравенстваПравила: 3) Обе части неравенства можно
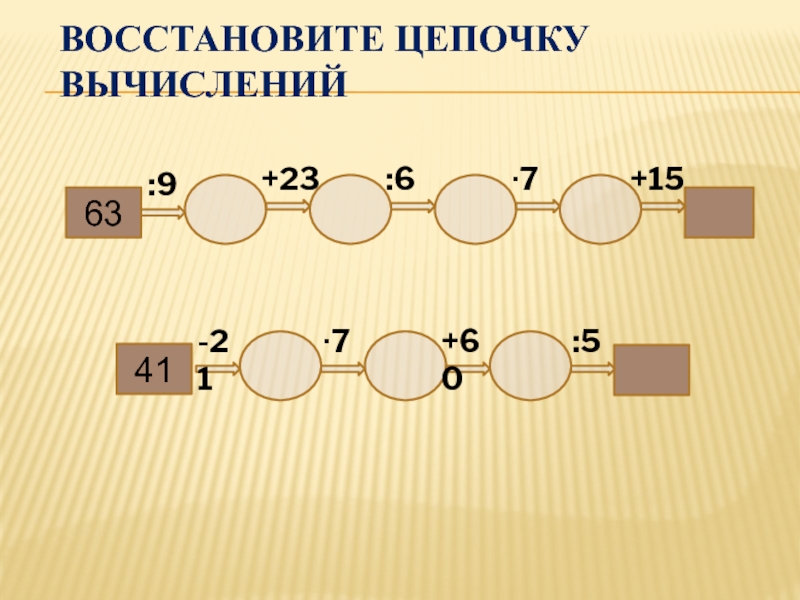
- 10. Слайд 10
- 11. Изобразите на координатной прямой промежуток (работаем
- 12. Решить у доски:с комментарием х + 4
- 13. Б) Неравенству х ≥ 15 соответствует
- 14. НАЙДИ ОШИБКУ! КОЛЛЕКТИВНАЯ РАБОТАРешить неравенство: 2х+4≥6; Решение:
- 15. Найди ошибку!Решить неравенство: 13х >16х+45Решение: 13х
- 16. Тестирование. (да - 1, нет- 0 )Является
- 17. 101010 Давайте проверим
- 18. Индивидуальная работа с поверкой у доскиВариант№ 1
- 19. Минутка отдыха
- 20. Самостоятельная работа(каждый за себя)4х > 16;
- 21. Взаимопроверка «5», если верно сделано
- 22. (4; + ∞)(-∞; 3][0; + ∞)(0 ; + ∞)(-∞; -2](21; + ∞)
- 23. Работа у доски: Решите систему неравенств
- 24. Решите систему неравенств:
- 25. Найди ошибку в решении неравенств и объясни
- 26. Итог урока - Какая задача стояла
- 27. Оценки Подведение итогов урока (выставляются оценки)Проанализируйте свою
- 28. Рефлексия.Продолжите фразу:Сегодня на уроке я узнал …Сегодня
- 29. Спасибо всем за работу! Человек не знающий
- 30. Домашнее задание подготовиться к контрольной работе
- 31. Спасибо завнимание
Математика учит преодолевать трудности и исправлять собственные ошибки. (Декарт).
Слайд 4
Задачи урока:
Повторить и обобщить знания учащихся по теме, продолжить формирование
умений работать по алгоритму
Развивать навыки коллективной работы, взаимопомощи, самоконтроля
Воспитывать математическую зоркость, культуру речи.
Развивать навыки коллективной работы, взаимопомощи, самоконтроля
Воспитывать математическую зоркость, культуру речи.
Слайд 5Линейные неравенства
Определения:
Запись вида а>в; а≥в или а
а≥в, а≤в называются
нестрогими.
Неравенства вида а>в, а<в называются
строгим
4) Решением неравенства с одной переменной называется то значение переменной, которое обращает его в верное числовое
неравенство
нестрогими.
Неравенства вида а>в, а<в называются
строгим
4) Решением неравенства с одной переменной называется то значение переменной, которое обращает его в верное числовое
неравенство
Слайд 7Линейные неравенства
Правила:
1) Любой член неравенства можно переносить из одной части неравенства
в другую, изменив его знак на противоположный, при этом знак неравенства не изменится.
Слайд 8Линейные неравенства
Правила:
2) Обе части неравенства можно умножить или разделить на одно
и тоже положительное число, при этом знак неравенства не изменится
Слайд 9Линейные неравенства
Правила:
3) Обе части неравенства можно умножить или разделить на
одно и тоже отрицательное число, при этом знак неравенства изменится на противоположный.
Слайд 11Изобразите на координатной прямой промежуток
(работаем в парах):
1) [-2;4]
2)
(-3;3)
3) (3;+∞)
4) (-∞;4]
5) (-5;+∞)
6) (0;7]
3) (3;+∞)
4) (-∞;4]
5) (-5;+∞)
6) (0;7]
а) х≥2
в) х≤3
с) х>8
д) х<5
е) -4<х<7
ж) -2≤х<6
Слайд 13
Б) Неравенству х ≥ 15
соответствует числовой промежуток
1) (– ∞; 15)
2) [15;
+∞)
3) (– ∞; 15]
4) (15;+∞)
3) (– ∞; 15]
4) (15;+∞)
Слайд 14НАЙДИ ОШИБКУ! КОЛЛЕКТИВНАЯ РАБОТА
Решить неравенство: 2х+4≥6;
Решение: 2х≥-2;
х≥-1;
-1 Х
Ответ: [-1;+∞).
-1 Х
Ответ: [-1;+∞).
Слайд 15Найди ошибку!
Решить неравенство: 13х >16х+45
Решение: 13х – 16х > 45
- 3х > 45
х > 15
15 х Ответ: х > 15 или (15; +∞)
15 х Ответ: х > 15 или (15; +∞)
Слайд 16Тестирование. (да - 1, нет- 0 )
Является ли число 12 решением
неравенства 2х>10?
2) Является ли число -6 решением неравенства 4х>12?
3) Является ли неравенство
5х-15>4х+14 строгим?
4) Существует ли целое число принадлежащее промежутку
[-2,8;-2,6]?
5) При любом ли значении переменной а верно неравенство
а² +4 >о?
6) Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число знак неравенства не меняется?
2) Является ли число -6 решением неравенства 4х>12?
3) Является ли неравенство
5х-15>4х+14 строгим?
4) Существует ли целое число принадлежащее промежутку
[-2,8;-2,6]?
5) При любом ли значении переменной а верно неравенство
а² +4 >о?
6) Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число знак неравенства не меняется?
Слайд 18Индивидуальная работа с поверкой у доски
Вариант№ 1
А) 0,6 – 2x
≤ 0,
Б) 2 + 6x > 5 + 7x
Вариант№ 2 А) 6 – 15x ≥ 0, Б) 4x + 7 ≤ 6x + 1 .
Вариант№ 2 А) 6 – 15x ≥ 0, Б) 4x + 7 ≤ 6x + 1 .
Слайд 20Самостоятельная работа(каждый за себя)
4х > 16;
2) – 3 x ≥ -9;
3) 15 a ≥ 0;
-7 x < 0;
5) - 6 – 5y ≥ 6 y + 16;
6) 1,4 a + 8,6 > - 20,8.
Слайд 21
Взаимопроверка
«5», если верно сделано 6 заданий
«4», если верно сделано 4
или 5 заданий
«3», если верно сделано 3 задания
«3», если верно сделано 3 задания
Слайд 25Найди ошибку в решении неравенств и объясни почему допущена ошибка.
31(2x+1)-12x >
50x
62x+31-12x > 50x
50x-50x > -31
0*x > -31
Ответ: х >0
62x+31-12x > 50x
50x-50x > -31
0*x > -31
Ответ: х >0
3(7-4y) > 3y-7
21 -12y > 3y-7
-12y + 3y > -7-21
-9y > - 28
y < 3 1/9
Ответ: (3 1/9 ;+ ∞)
Слайд 26
Итог урока
- Какая задача стояла перед нами в начале урока?
- Что
нового вы узнали?
- Что мы повторили?
- Что понравилось, что хотели бы изменить, чтобы было интересно?
- Что было непонятно?
- Что мы повторили?
- Что понравилось, что хотели бы изменить, чтобы было интересно?
- Что было непонятно?
Слайд 27Оценки Подведение итогов урока (выставляются оценки)
Проанализируйте свою работу на уроке и
поставьте себе оценку «5» - все понимаю; «4»- понимаю, но есть вопросы; «?» -затрудняюсь решать неравенства
Слайд 28Рефлексия.
Продолжите фразу:
Сегодня на уроке я узнал …
Сегодня на уроке я научился
…
Сегодня на уроке я познакомился …
Сегодня на уроке я повторил …
Сегодня на уроке я закрепил …
Сегодня на уроке я познакомился …
Сегодня на уроке я повторил …
Сегодня на уроке я закрепил …
Слайд 29Спасибо всем за работу!
Человек не знающий математики, не способен ни к
каким другим наукам. Более того, он даже не способен оценить уровень своего невежества.»
Роджер Бэкон. (1214-1294г)
Роджер Бэкон. (1214-1294г)










![Презентация по математике на темуРешение неравенств с одной переменной и их систем(8 класс) Изобразите на координатной прямой промежуток (работаем в парах):1) [-2;4] 2) (-3;3) Изобразите на координатной прямой промежуток (работаем в парах):1) [-2;4] 2) (-3;3) 3) (3;+∞)](/img/thumbs/dd296c231d873608fb939f444ade5d50-800x.jpg)










![Презентация по математике на темуРешение неравенств с одной переменной и их систем(8 класс) (4; + ∞)(-∞; 3][0; + ∞)(0 ; + ∞)(-∞; -2](21; + ∞) (4; + ∞)(-∞; 3][0; + ∞)(0 ; + ∞)(-∞; -2](21; + ∞)](/img/tmb/8/712037/e24078a05fe9f9f3d2646c4c44aeafa0-800x.jpg)