- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на темукомбинаторика (9 класс)
Содержание
- 1. Презентация по математике на темукомбинаторика (9 класс)
- 2. Не нужно нам владеть клинком, Не ищем
- 3. Обобщающий урок по теме «Элементы комбинаторики»
- 4. Цель урока: Систематизировать изученный материал;Развивать математическое мышление.
- 5. I. Фронтальный опросХод урока
- 6. Вопрос 1 : Как обозначается произведение
- 7. Вопрос 2 : Что называется размещением?
- 8. Решите задачуУчащиеся 9 класса изучают 10 предметов.
- 9. Вопрос 3 : Что называется перестановками?
- 10. Решите задачу:Сколькими способами могут сесть в автомобиль
- 11. Вопрос 4. Что называется сочетаниями? Как
- 12. Решите задачуВ классе 25 учеников. Сколькими способами можно из них выбрать 4 учащихся для дежурства?Решение:Ответ:12650
- 13. II. Решение задач в группах с последующим обсуждением.
- 14. 1.Вычислить: а) 3! б)5!2.В конкурсе участвуют
- 15. 4. Сколькими способами можно составить трехцветный полосатый
- 16. III. Подведение итогов урока
- 17. Устные упражнения: 1. Делится ли число 30!
- 18. Задачи для домашней зачетной работы по теме
- 19. 1–я группа На тренировке занимаются 12 баскетболистов.
- 20. 2-я группа Сколько различных трехзначных чисел можно
- 21. 3-я группа Во скольких девятизначных числах все
- 22. Ответы и решения.1-я группа
- 23. Ответы и решения.2-я группа
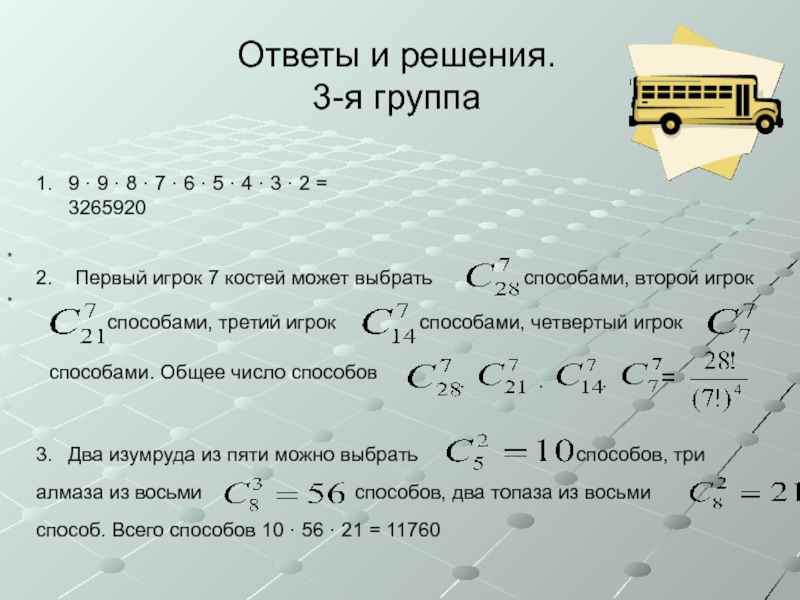
- 24. Ответы и решения.3-я группа**
- 25. Контрольная работа по теме:«Элементы комбинаторики» Цель: выявить
- 26. I– вариантИз 30 участников собрание надо выбрать
- 27. 4. В классе учатся 16 мальчиков
- 28. II– вариантСколькими способами может разместиться семья из
- 29. В библиотеке читателю предложили на выбор 10
- 30. РешенияI– варианта (способов) (способов)
- 31. РешенияII– варианта
- 32. Ответы:I вариант870504056400400600II вариант244032021072096
Не нужно нам владеть клинком, Не ищем славы громкой. Тот побеждает, кто знаком С искусством мыслить тонким
Слайд 2Не нужно нам владеть клинком, Не ищем славы громкой. Тот побеждает, кто знаком
С искусством мыслить тонким
Уордсворд
Слайд 6Вопрос 1 :
Как обозначается произведение чисел от 1 до n?
Ответ:
Произведение всех натуральных чисел от 1 до n обозначается n! (n! =1 · 2 · 3…n)
Слайд 7Вопрос 2 :
Что называется размещением?
По какой формуле вычисляется размещение?
Ответ:
Размещением из n объектов по k называют любой выбор к объектов, взятых в определенном порядке из n объектов.
Число размещений из n объектов по k
обозначают и вычисляют по формуле:
Слайд 8Решите задачу
Учащиеся 9 класса изучают 10 предметов. Сколькими способами можно составить
расписание уроков на один день так, чтобы было 6 различных уроков?
Решение:
A6 10= 10 · 9 · 8 · 7 · 6 · 5=151.200
Ответ: 151.200
Слайд 9Вопрос 3 : Что называется перестановками? Как обозначаются перестановки? По какой
формуле вычисляются перестановки?
Ответ:
Размещения из n э лементов по n называются перестановками.
Обозначение: P n
Ф ормула для вычисления перестановок:
P n = A6 10 =n ·(n -1) · (n-2) · … · 3 · 2 · 1=n!
Слайд 10Решите задачу:
Сколькими способами могут сесть в автомобиль 5 человек, каждый из
которых может быть водителем?
Решение:
P5 = A55 = 5! = 1 · 2 · 3 · 4 · 5 = 120
Слайд 11Вопрос 4. Что называется сочетаниями? Как обозначаются сочетания и по какой
формуле производятся вычисления?
Ответ:
Сочетаниями из n объектов по k называют любой выбор k объектов, взятых из n объектов.
Обозначение:
Формула для вычисления сочетаний:
Слайд 12Решите задачу
В классе 25 учеников. Сколькими способами можно из них выбрать
4 учащихся для дежурства?
Решение:
Ответ:12650
Слайд 141.Вычислить: а) 3! б)5!
2.В конкурсе участвуют 20 человек. Сколькими способами
можно присудить первую, вторую и третью премии?
Решение:
а) 3! = 1 · 2 · 3 =6
б) 5! = 1 · 2 · 3 · 4 · 5 = 120
Решение:
A3 20=20 · 19 · 18=6840
Слайд 154. Сколькими способами можно составить трехцветный полосатый флаг, если имеются ткани
6 цветов?
3. Сколько перестановок можно получить из букв, составляющих слово «апельсин».
Решение: P n=5!=1 · 2 · 3 · 4 · 5=120
Решение:
Слайд 17Устные упражнения:
1. Делится ли число 30! на:
а) 90 б) 92
в) 94 г) 96 ?
2. Найти значение выражения:
а) б) в)
3. Что больше: 6! · 5 или 5! · 6
2. Найти значение выражения:
а) б) в)
3. Что больше: 6! · 5 или 5! · 6
Слайд 18Задачи
для домашней зачетной работы
по теме
«Элементы комбинаторики»
1 группа –
«слабые»
2 группа – «средние»
3 группа – «сильные»
2 группа – «средние»
3 группа – «сильные»
Слайд 191–я группа
На тренировке занимаются 12 баскетболистов. Сколько может быть образовано тренером
различных стартовых пятерок?
Сколько разных слов можно составить из слова «комбинаторика»?
Для составления букета из девяти цветов в магазине имеются розы, гвоздики, хризантемы и пионы. Сколькими способами можно составить из этих цветов букет?
Сколько существует четырехзначных номеров, не содержащих цифр 0, 5, 8?
Сколько разных слов можно составить из слова «комбинаторика»?
Для составления букета из девяти цветов в магазине имеются розы, гвоздики, хризантемы и пионы. Сколькими способами можно составить из этих цветов букет?
Сколько существует четырехзначных номеров, не содержащих цифр 0, 5, 8?
Слайд 202-я группа
Сколько различных трехзначных чисел можно составить из цифр 1, 2,
3, 4 и 5 при условии, что ни одна цифра не повторится?
Сколько чисел меньше миллиона можно записать при помощи цифр 8 и 9?
В магазине имеются в продаже яблоки, апельсины, груши и мандарины. Сколькими способами можно образовать набор из 12 фруктов?
Сколько чисел меньше миллиона можно записать при помощи цифр 8 и 9?
В магазине имеются в продаже яблоки, апельсины, груши и мандарины. Сколькими способами можно образовать набор из 12 фруктов?
Слайд 213-я группа
Во скольких девятизначных числах все цифры различны?
Между четырьмя игроками
в домино поровну распределяется 28 костей. Сколькими способами могут распределяться кости домино( очередность выбора костей не влияет на результат).
У ювелира есть пять изумрудов. Сколькими способами он может сделать браслет, включив в него два изумруда, три алмаза и два топаза?
У ювелира есть пять изумрудов. Сколькими способами он может сделать браслет, включив в него два изумруда, три алмаза и два топаза?
Слайд 25Контрольная работа по теме:
«Элементы комбинаторики»
Цель: выявить степень усвоения учащимися изученного
материалами и проанализировать ошибки, допущенные учащимися с целью дальнейшего их устранения: развивать навыки самостоятельной работы.
Слайд 26I– вариант
Из 30 участников собрание надо выбрать председателя и секретаря. Сколькими
способами это можно сделать?
Курьер должен развести пакеты в 7 различных учреждений. Сколько маршрутов он может выбрать?
В магазине «Филателия» продается 8 различных наборов марок посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Курьер должен развести пакеты в 7 различных учреждений. Сколько маршрутов он может выбрать?
В магазине «Филателия» продается 8 различных наборов марок посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Слайд 274. В классе учатся 16 мальчиков и 12 девочек. Для
уборки территории требуется выделить 4 мальчика и 3 девочки. Сколькими способами это можно сделать?
5. Сколько шестизначных чисел (без повторения цифр) можно составить из цифр 0, 3, 5, 6, 7, 8?
5. Сколько шестизначных чисел (без повторения цифр) можно составить из цифр 0, 3, 5, 6, 7, 8?
Слайд 28II– вариант
Сколькими способами может разместиться семья из трех человек в четырехместном
купе, если других пассажиров в купе нет?
Сколькими способами 8 человек могут встать в очередь в театральную кассу?
Учащимся дали список из 10 книг, которые нужно прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?
Сколькими способами 8 человек могут встать в очередь в театральную кассу?
Учащимся дали список из 10 книг, которые нужно прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?
Слайд 29В библиотеке читателю предложили на выбор 10 книг и 4 журнала.
Сколькими способами он может выбрать из них 3 книги и 2 журнала?
Сколько пятизначных чисел (без повторения цифр) можно составить из цифр 0, 2, 5, 6, 7?
.
Сколько пятизначных чисел (без повторения цифр) можно составить из цифр 0, 2, 5, 6, 7?
.
