- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Задания ЕГЭ 2014 года (11 класс)
Содержание
- 1. Презентация по математике на тему Задания ЕГЭ 2014 года (11 класс)
- 2. С1критерии,типичные ошибки;3. С2критерии,типичные ошибки;4. С3критерии,типичные ошибки;5. С4критерии,типичные ошибки;6. С5критерии,типичные ошибки;7. С6критерии,типичные ошибки
- 3. С1
- 4. Решение. С1
- 5. Слайд 5
- 6. Типичные ошибки, допущенные учащимися в заданиях С1:при
- 7. С2
- 8. С2
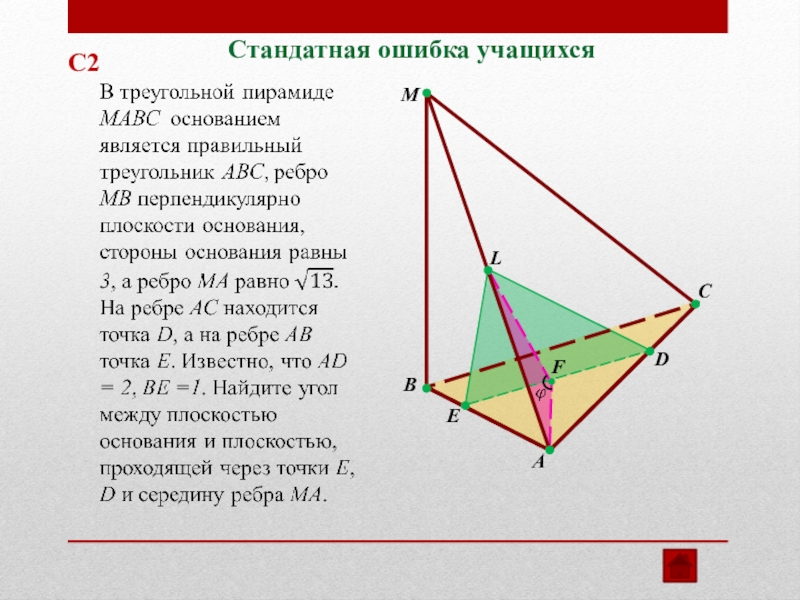
- 9. DELMBACFСтандатная ошибка учащихсяС2
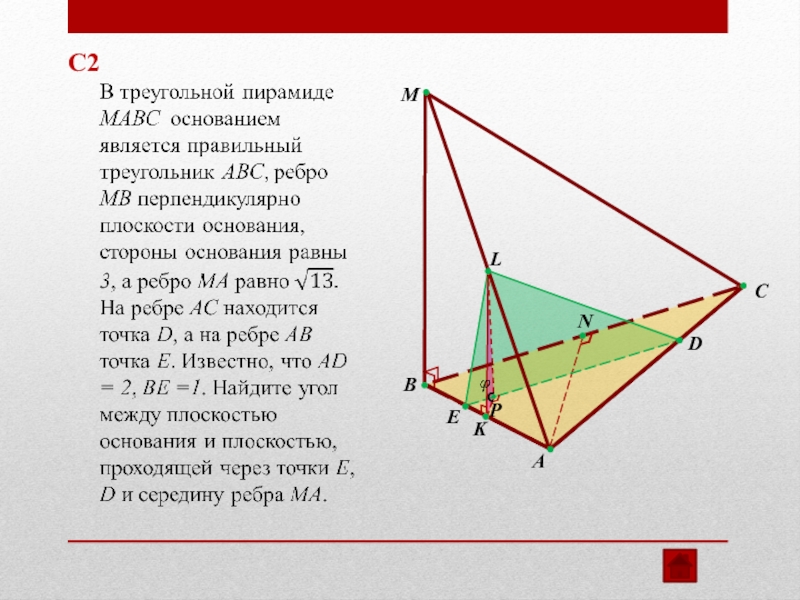
- 10. PELMBACDKNС2
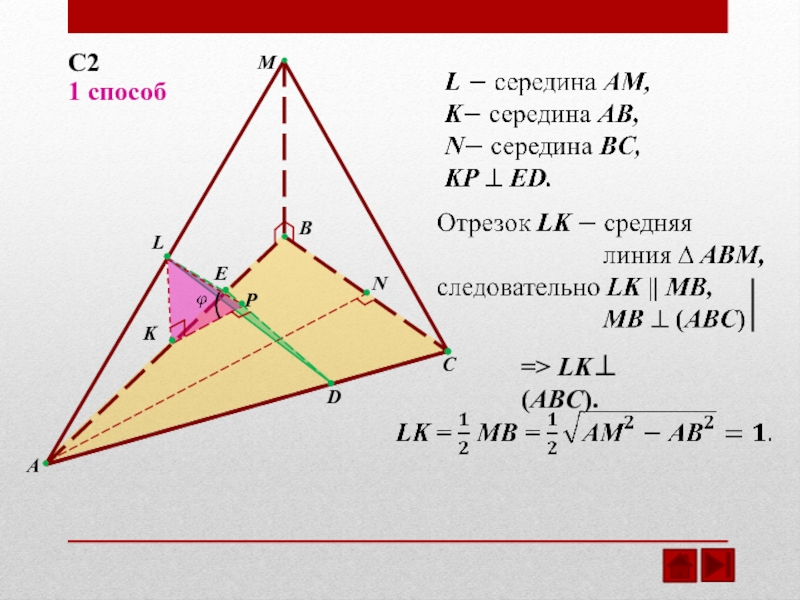
- 11. PELMBACDKN1 способС2
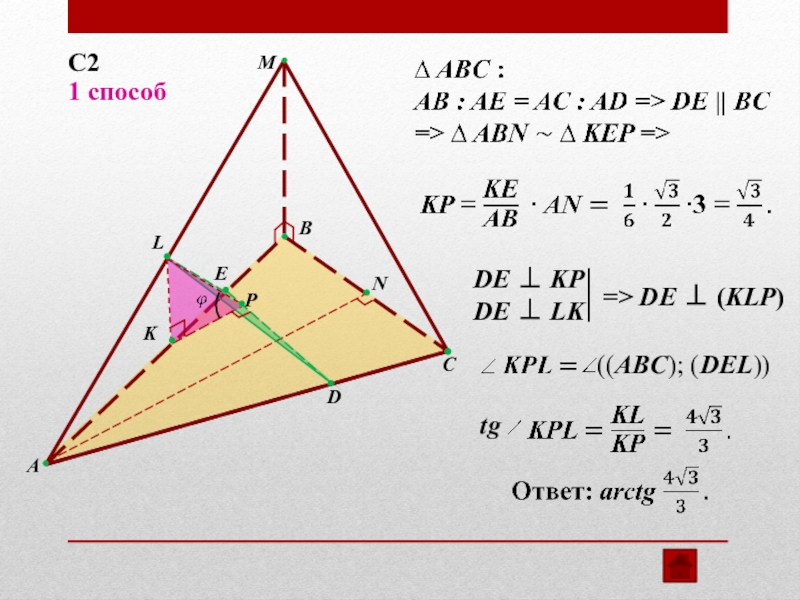
- 12. PELMBACDKN1 способС2
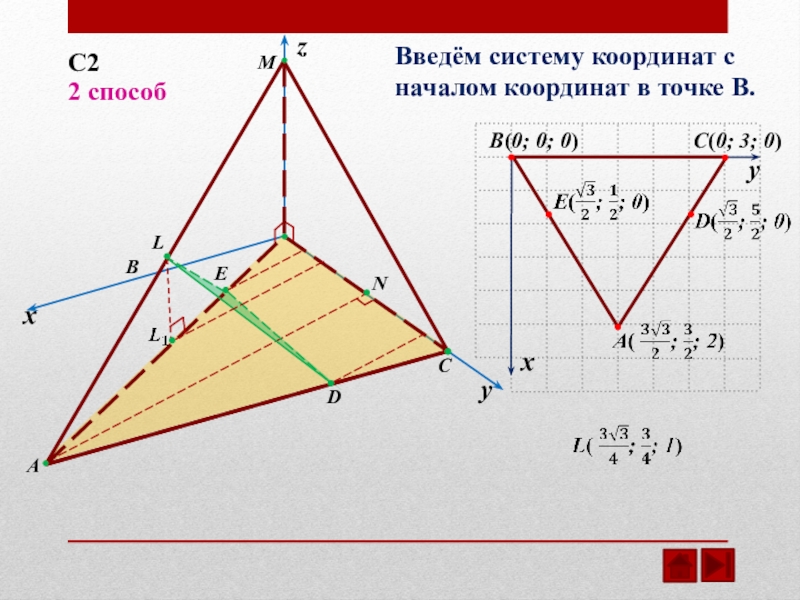
- 13. CELMBADNxyzВведём систему координат с началом координат в точке B.B(0; 0; 0)C(0; 3; 0)xy2 способС2
- 14. MNxyzУгол между плоскостями равен углу между прямыми,
- 15. Слайд 15
- 16. Слайд 16
- 17. GFDELMBACKNДостроим пирамиду MABCDдо правильной треугольнойпризмы и построим её сечениеплоскостью DEL.3 способС2
- 18. GFDPELMBACKN=>3 способС2
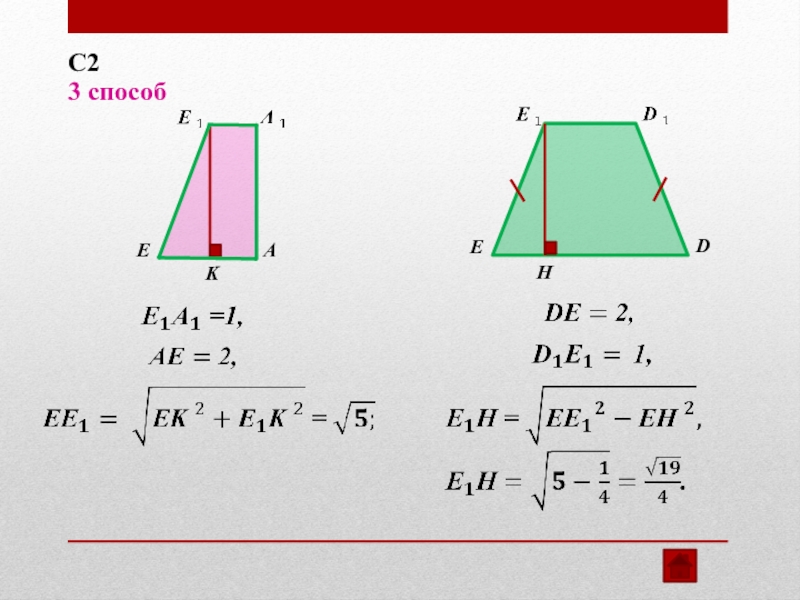
- 19. DEH3 способС2 AEK
- 20. DEH3 способС2 GFDEJ
- 21. 3 способС2
- 22. С этими заданиями в 2014 году
- 23. С3 Решение.1. Первое неравенство
- 24. С3 1 случай
- 25. С3 2 случайРешение второго неравенстваисходной системы:
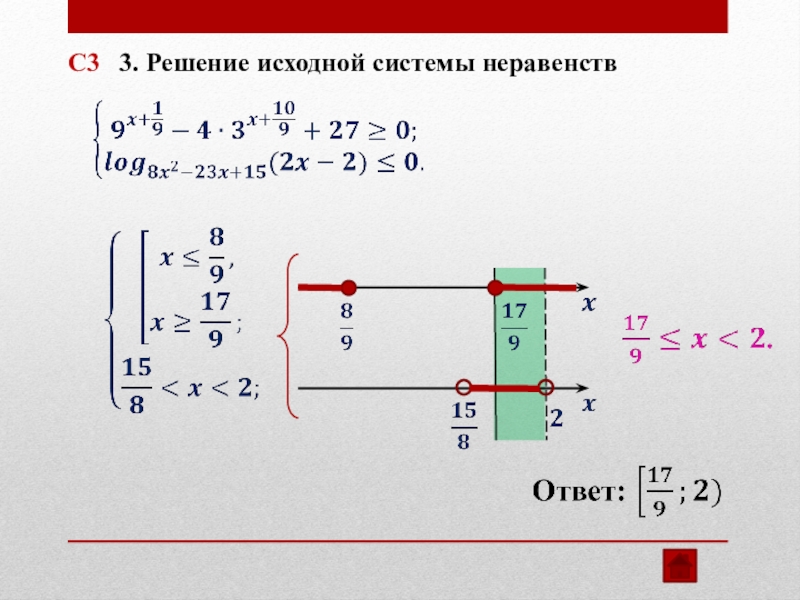
- 26. 3. Решение исходной системы неравенств С3
- 27. С3
- 28. Типичные ошибки учащихся, допущенные в заданиях С3:при
- 29. С4 Одна окружность вписана в прямоугольную трапецию,
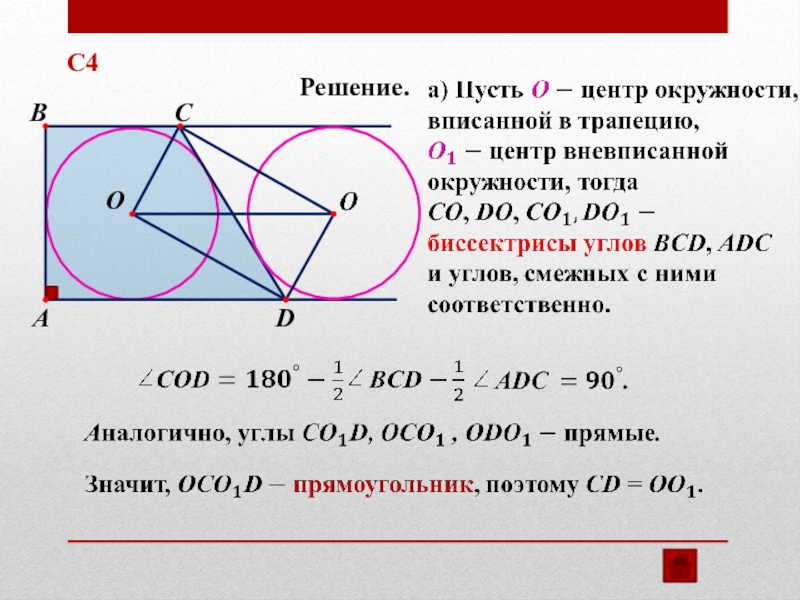
- 30. AС4 BCDOРешение.
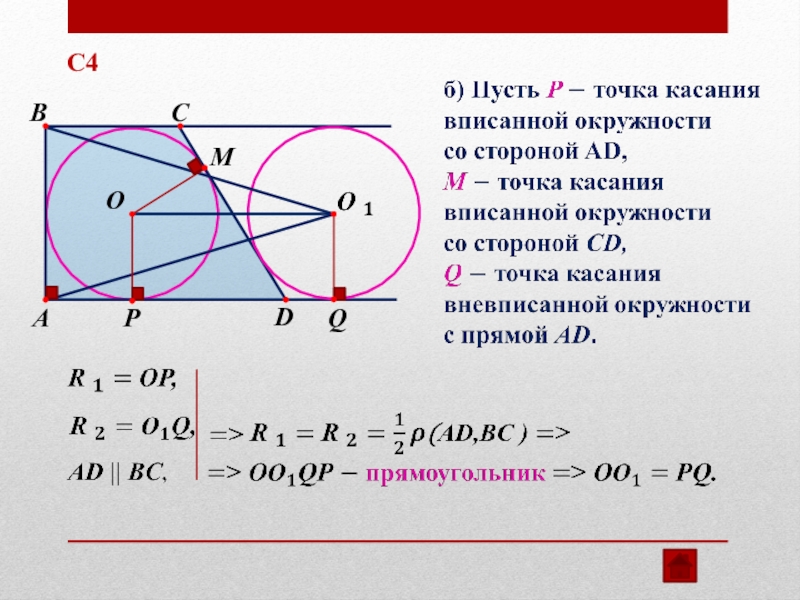
- 31. MPQAС4 BCOD
- 32. AQDPС4 BCOM
- 33. AQDPС4 BCOM
- 34. С4
- 35. Типичные ошибки учащихся, допущенные в заданиях С4:при
- 36. С5 Решение.(1)(2)
- 37. Исходное уравнение будет иметь ровно два решения,
- 38. 1) Исследуем количество корней уравнения С5
- 39. 2) Исследуем количество корней уравнения С5
- 40. 3) Выясним при каких значениях а уравнения С5 будут иметь общие решения.
- 41. С5 aa(1)(2)00222222211222211a02Исходное уравнение имеет ровно два решения приКол-во решенийКол-во решений
- 42. С5
- 43. Типичные ошибки учащихся, допущенные в заданиях С5:при
- 44. Про некоторый
- 45. С6 Решение.
- 46. С6 Решение.b) Может ли одним из
- 47. С6 Решение.с) Какое наименьшее возможное значение может принимать сумма чисел такого набора?
- 48. С6 Решение.с) Какое наименьшее возможное значение может
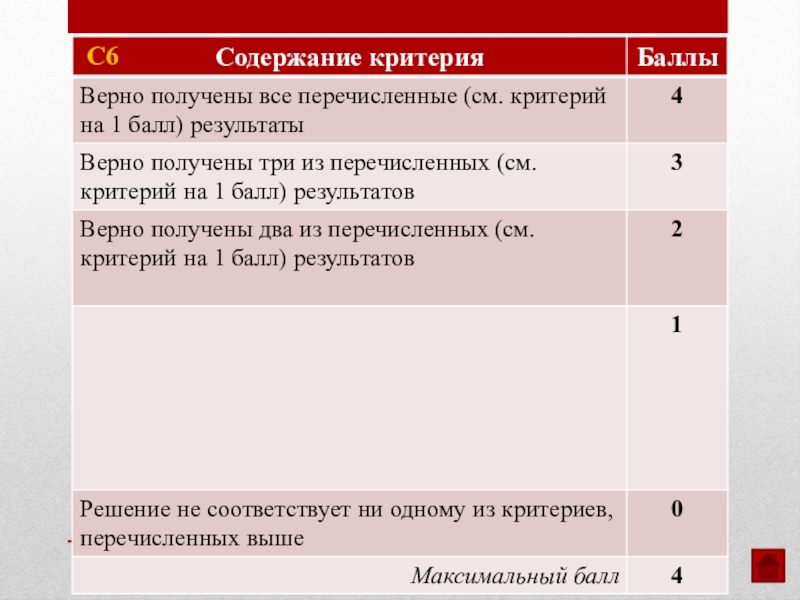
- 49. С6
- 50. Типичные ошибки учащихся, допущенные в заданиях С6:отсутствие
Слайд 1Анализ результатов
ЕГЭ по математике
в 2014 году
Тихомирова Галина Юрьевна МБОУ «СОШ
Слайд 2С1
критерии,
типичные ошибки;
3. С2
критерии,
типичные ошибки;
4. С3
критерии,
типичные ошибки;
5. С4
критерии,
типичные ошибки;
6. С5
критерии,
типичные ошибки;
7. С6
критерии,
типичные
Слайд 6Типичные ошибки, допущенные учащимися в заданиях С1:
при применении формул приведения;
при решении
при нахождении корней данного уравнения, принадлежащих заданному отрезку;
потеря корней при решении уравнения разложением на множитнли
вычислительные ошибки.
С этими заданиями в 2014 году справились 7,37% учащихся (2 балла),
11,91% учащихся (1 балл).
Слайд 13C
E
L
M
B
A
D
N
x
y
z
Введём систему координат с началом координат в точке B.
B(0; 0; 0)
C(0;
x
y
2 способ
С2
Слайд 14M
N
x
y
z
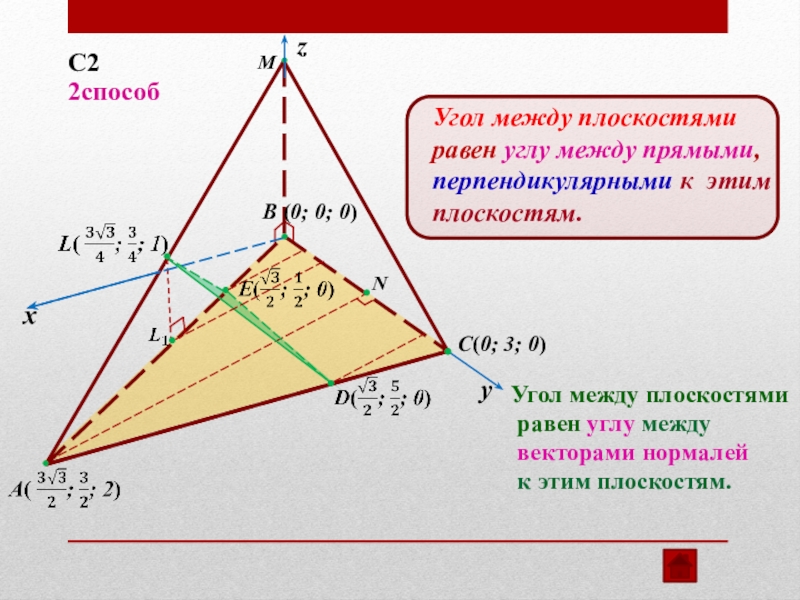
Угол между плоскостями
равен углу между прямыми, перпендикулярными к этим плоскостям.
Угол между плоскостями
равен углу между
векторами нормалей
к этим плоскостям.
B (0; 0; 0)
C(0; 3; 0)
2способ
С2
Слайд 17G
F
D
E
L
M
B
A
C
K
N
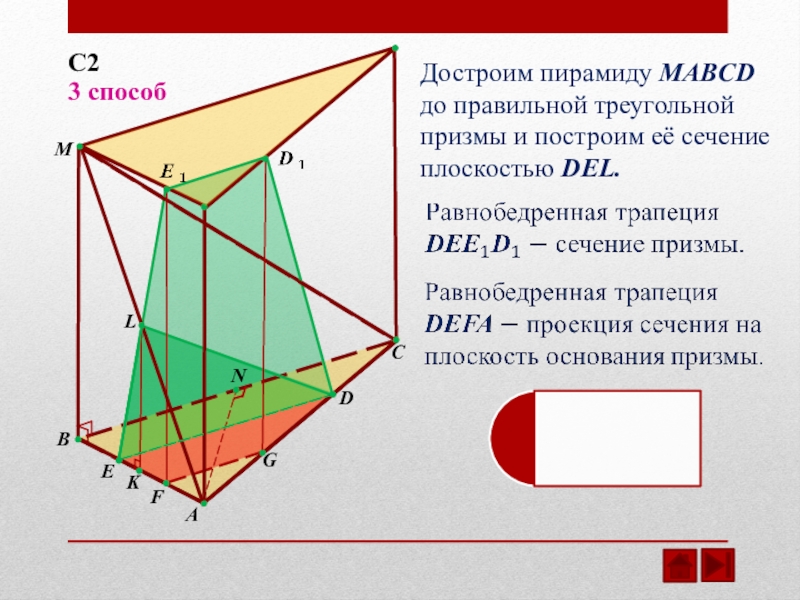
Достроим пирамиду MABCD
до правильной треугольной
призмы и построим её сечение
плоскостью DEL.
3 способ
С2
Слайд 22 С этими заданиями в 2014 году справились
0,38% учащихся (2
0.79% учащихся (1 балл).
Типичные ошибки, допущенные учащимися в заданиях С2:
при построении угла между плоскостями;
при проецировании точек на плоскость;
при решении простейшей планиметрической задачи;
при определении координат точек и векторов;
при вычислении искомых величин.
Слайд 28Типичные ошибки учащихся, допущенные в заданиях С3:
при выполнении преобразований неравенств;
при нахождении
при решении показательного неравенства;
при выборе решений исходной системы неравенств;
вычислительные ошибки.
С этими заданиями в 2014 году справились
1,69% учащихся (3 балла),
0,47% учащихся (2 балла),
4.35% учащихся (1 балл).
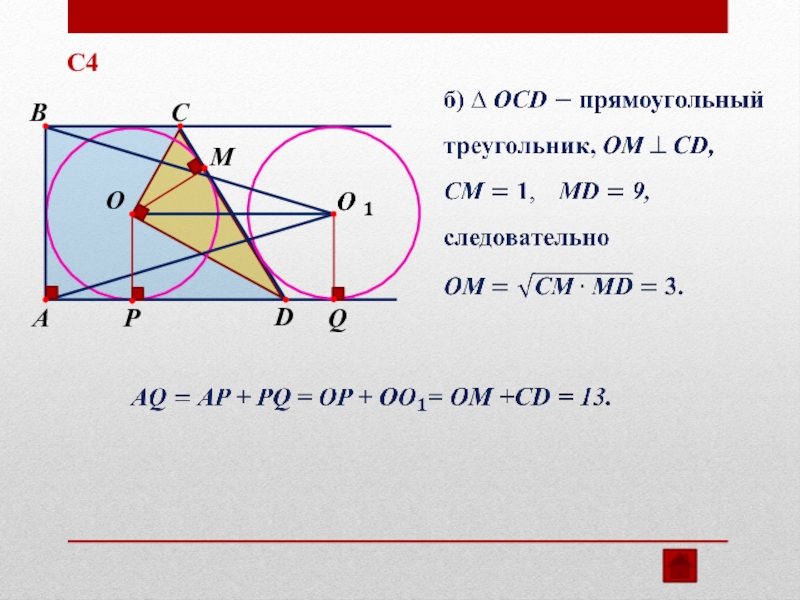
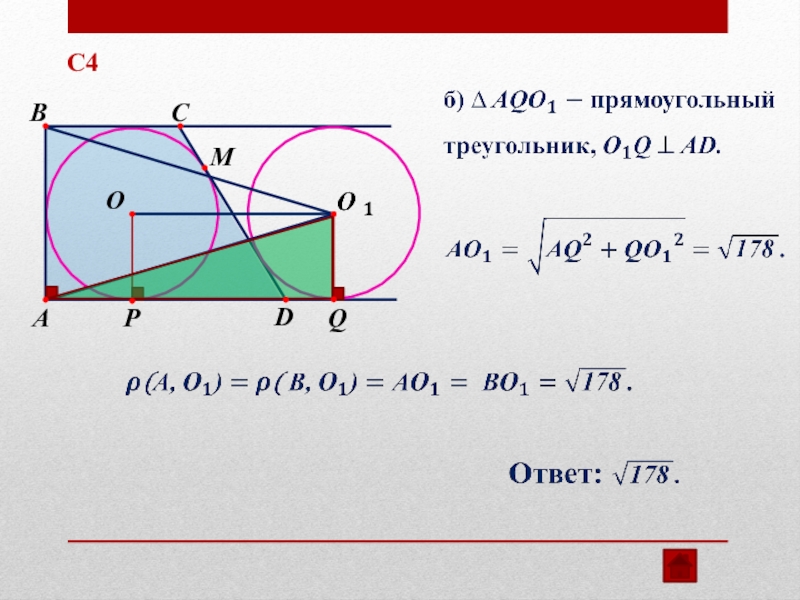
Слайд 29С4
Одна окружность вписана в прямоугольную трапецию, а вторая касается большей
а) Докажите, что расстояние между центрами окружностей равно большей боковой стороне трапеции.
б) Найдите расстояние от вершины одного из прямых углов трапеции до центра второй окружности, если точка касания первой окружности с большей боковой стороной трапеции делит её на отрезки, равные 1 и 9.
Слайд 35Типичные ошибки учащихся, допущенные в заданиях С4:
при рассмотрении комбинаций:
вневписанная окружность и трапеция;
при нахождении значения искомой величины;
вычислительные ошибки.
С этими заданиями в 2014 году справились
0,25% учащихся (3 балла),
0,08% учащихся (2 балла),
0,39% учащихся (1 балл).
Слайд 37Исходное уравнение будет иметь ровно два решения, если:
1) оба уравнения имеют
2) одно из уравнений имеет два решения, а другое не имеет решений,
3) оба уравнения имеют по два решения и эти решения соответственно равны.
Слайд 41
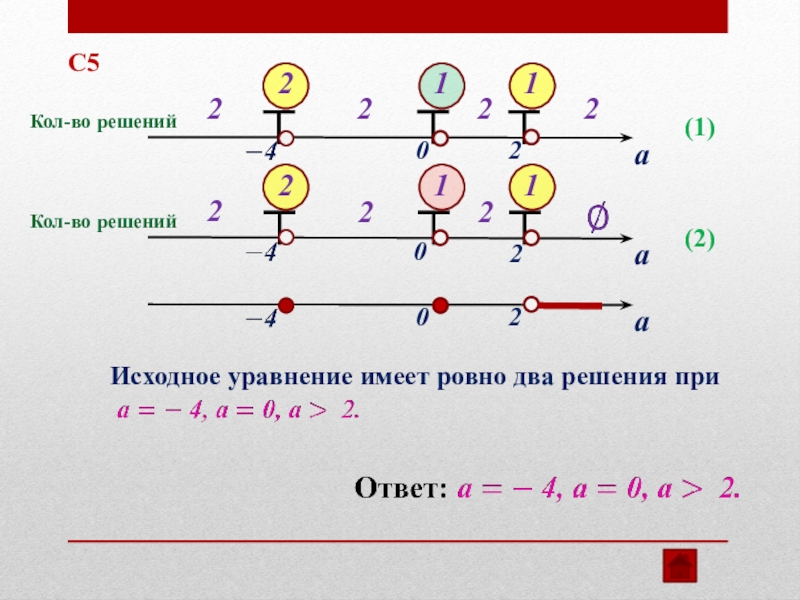
С5
a
a
(1)
(2)
0
0
2
2
2
2
2
2
2
1
1
2
2
2
2
1
1
a
0
2
Исходное уравнение имеет ровно два решения при
Кол-во решений
Кол-во решений
Слайд 43Типичные ошибки учащихся, допущенные в заданиях С5:
при составлении условий на параметр
были приобретены посторонние значения,
либо часть верных значений была потеряна;
при исследовании квадратных уравнений;
вычислительные ошибки
С этими заданиями в 2014 году справились
0,02% учащихся (4 балла),
0,00% учащихся (3 балла),
0,06% учащихся (2 балла),
1,18% учащихся (1 балл).
Слайд 44 Про некоторый набор, состоящий из 11
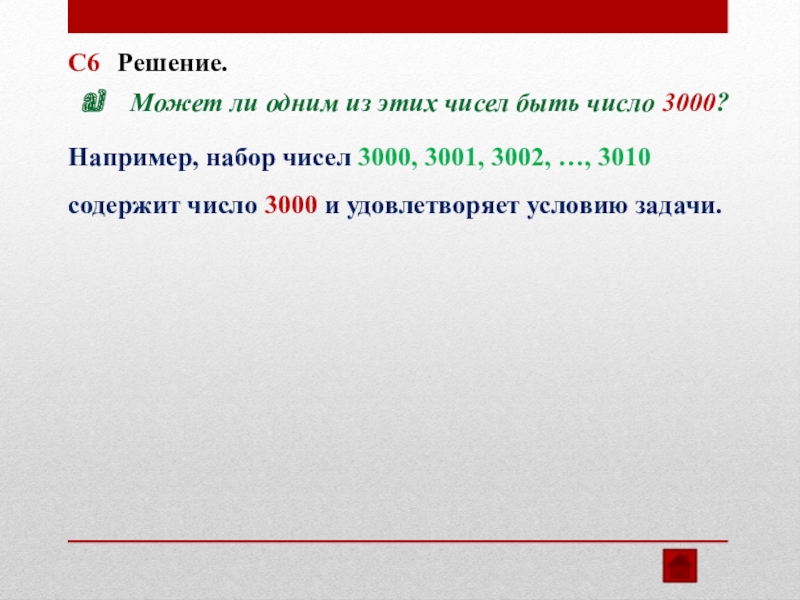
Может ли одним из этих чисел быть число 3000?
Может ли одним из этих чисел быть число 16?
Какое наименьшее возможное значение может принимать сумма чисел такого набора?
С6
Слайд 46С6
Решение.
b) Может ли одним из этих чисел быть число
Складывая эти неравенства, получаем:
Последнее неравенство противоречит условию задачи.
Значит среди чисел нет числа 16.
Слайд 47С6
Решение.
с) Какое наименьшее возможное значение может
принимать сумма чисел такого
Слайд 48С6
Решение.
с) Какое наименьшее возможное значение может
принимать сумма чисел такого
Рассмотрим набор 17, 18, …, 27. Сумма любых трёх
чисел этого набора не меньше 17 + 18 + 19 = 54,
а сумма любых двух не превосходит 26 + 27 = 53.
Значит этот набор удовлетворяет условию и имеет
Наименьшую сумму чисел среди таких наборов.
Эта сумма равна 242.
Ответ: а) да, b) нет, с) 242.
Слайд 50Типичные ошибки учащихся, допущенные в заданиях С6:
отсутствие обоснованного решения в пункте
доказательство того факта, что в наборе нет чисел, меньших 17, в п. в;
вычислительные ошибки.
С этими заданиями в 2014 году справились
0,14% учащихся (4 балла),
0,19% учащихся (3 балла),
0,75% учащихся (2 балла),
1,84% учащихся (1 балл).