- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Задачки из ЕГЭ №20
Содержание
- 1. Презентация по математике на тему Задачки из ЕГЭ №20
- 2. Задание:Экзамен включает 30 заданий. За каждое верно
- 3. Задание:Улитка за день залезает вверх по дереву
- 4. Задание:В корзине лежат 30 грибов: рыжики и
- 5. 3адание: Саша пригласил Петю в гости, сказав,
- 6. Задание:Список заданий викторины состоял из 25 вопросов.
- 7. Задание:Из книги выпало несколько идущих подряд листов.
- 8. Задание: Десять столбов соединены между собой проводами
- 9. Задание: В конце четверти Петя выписал подряд
- 10. Задание: Среднее арифметическое 6 различных натуральных чисел
- 11. Задание:Прямоугольник разбит на четыре маленьких прямоугольника двумя
- 12. Слайд 12
- 13. Задание: На поверхности глобуса фломастером проведены 17
- 14. Слайд 14
- 15. Задание: Хозяин договорился с рабочими, что они
- 16. Задание: Маша и Медведь съели 100 печений
- 17. Задание:На палке отмечены поперечные линии красного, жёлтого
- 18. Задание :На прилавке цветочного магазина стоят 3
- 19. Задание:На кольцевой дороге расположены четыре бензоколонки: A,
- 20. Слайд 20
- 21. Задание:Во всех подъездах дома одинаковое число этажей,
- 22. Задание: В таблице три столбца и несколько
- 23. Задание:Три луча, выходящие из одной точки, разбивают
- 24. В обменном пункте можно совершить одну из
- 25. Сколькими способами можно выложить в ряд три
- 26. Слайд 26
- 27. Альпинист поднимается на гору высотой 300300 метров. Первые 5050 метров он
- 28. В лотке 30 яиц: белые и рябые.
- 29. Слайд 29
- 30. Слайд 30
Слайд 2Задание:
Экзамен включает 30 заданий. За каждое верно выполненное задание ученик получает
Решение:
Пусть x заданий решено верно, y — с ошибкой и n — не решено вообще. Тогда всего задач x+y+n=30, и получено баллов 3x+2y=44.
Подставив x=30-n-y во второе уравнение получим: 5y=46-3n.
Выбираем значение n таким, чтобы количество ошибок было максимально и y осталось целым числом, т.е. n=2.
5y=46-3⋅2=40.
y=8 — максимальное количество ошибок с результатом 44 балла
Ответ: 8
Слайд 3Задание:
Улитка за день залезает вверх по дереву на 2 м, а
Ответ: 8
Решение:
Заметим, что в этой задаче следует различать понятие "сутки" и понятие "день".
В задаче спрашивается именно за сколько дней улитка доползет до вершины дерева.
За один день улитка поднимается на 2 м, а за одни сутки улитка поднимается на 1 м (за день поднимается на 2 м, а потом за ночь спускается на 1 м).
За 7 суток улитка поднимается на 7 метров. То есть утром 8-го дня ей останется доползти до вершины 2 м. И за восьмой день она преодолеет это расстояние.
Слайд 4Задание:
В корзине лежат 30 грибов: рыжики и грузди. Известно, что среди
Решение:
Так как среди любых 12 грибов имеется хотя бы один рыжик (или больше) число груздей должно быть меньше или равно чем 12-1=11
Отсюда следует, что число рыжиков больше или равно чем 30-11=19
Так как среди любых 20 грибов хотя бы один груздь (или больше), число рыжиков должно быть меньше или равно чем 20-1=19
Тогда получили, что с одной стороны, число рыжиков больше или равно чем 19, а с другой - меньше или равно чем 19.
Следовательно, число рыжиков равно 19.
Ответ: 19
Слайд 53адание:
Саша пригласил Петю в гости, сказав, что живёт в седьмом
Ответ: 2
Слайд 6Задание:
Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ
Ответ: 17
Слайд 7Задание:
Из книги выпало несколько идущих подряд листов. Номер последней страницы перед
Ответ: 85
Слайд 8Задание:
Десять столбов соединены между собой проводами так, что от каждого
Ответ: 40
Слайд 9Задание:
В конце четверти Петя выписал подряд все свои отметки по
Ответ: 3
Слайд 10Задание:
Среднее арифметическое 6 различных натуральных чисел равно 8. На сколько
Ответ: 6
Слайд 11Задание:
Прямоугольник разбит на четыре маленьких прямоугольника двумя прямолинейными разрезами. Площади трех
Ответ: 20
Слайд 13Задание:
На поверхности глобуса фломастером проведены 17 параллелей и 24 меридиана.
Ответ: 432
Слайд 15Задание:
Хозяин договорился с рабочими, что они копают колодец на следующих
Ответ: 89100
Слайд 16Задание:
Маша и Медведь съели 100 печений и банку варенья, начав
Ответ: 90
Слайд 17Задание:
На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если
Ответ: 21
Слайд 18Задание :
На прилавке цветочного магазина стоят 3 вазы с розами: оранжевая,
Ответ: 7
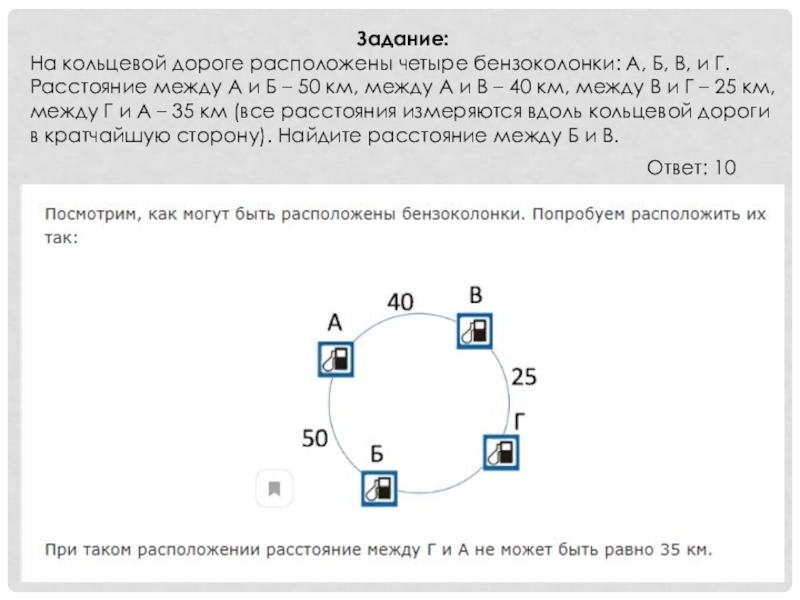
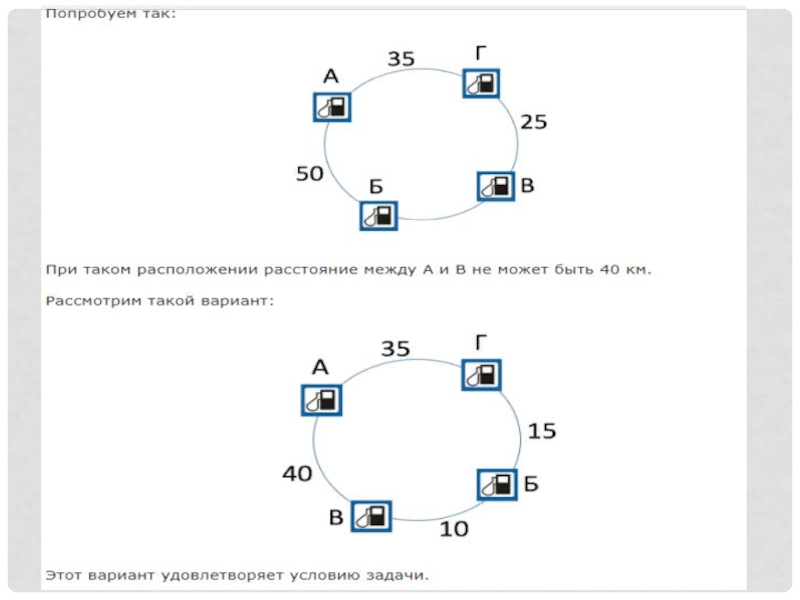
Слайд 19Задание:
На кольцевой дороге расположены четыре бензоколонки: A, Б, B, и Г.
Ответ: 10
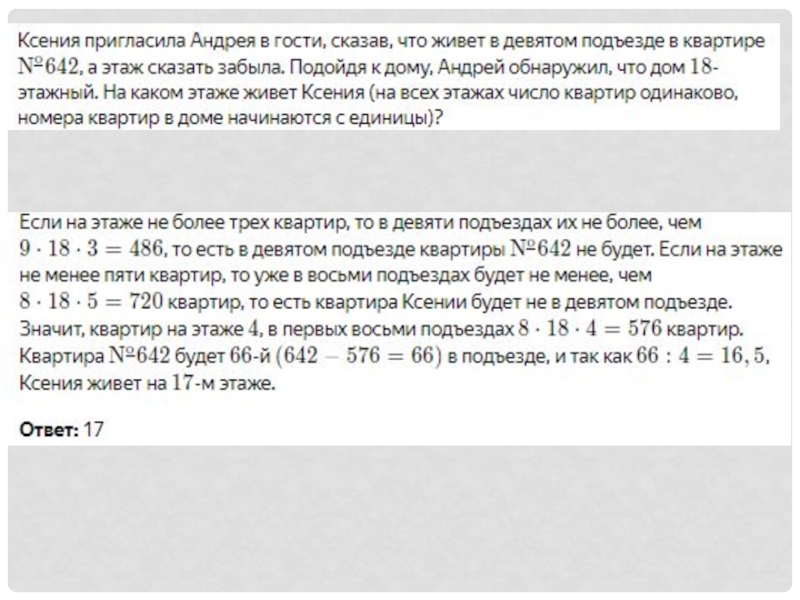
Слайд 21Задание:
Во всех подъездах дома одинаковое число этажей, а на каждом этаже
Ответ: 7
Слайд 22Задание:
В таблице три столбца и несколько строк. В каждую клетку
Ответ:17
Слайд 23Задание:
Три луча, выходящие из одной точки, разбивают плоскость на три разных
Ответ: 20
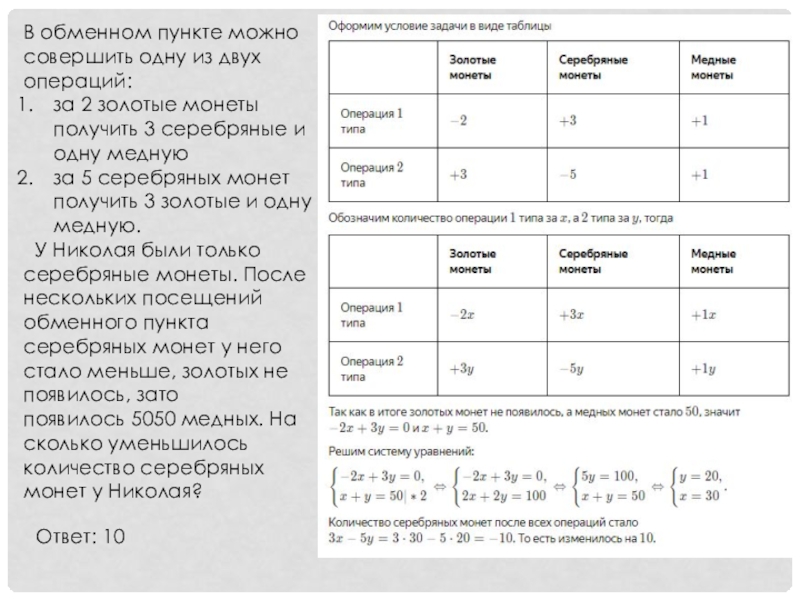
Слайд 24В обменном пункте можно совершить одну из двух операций:
за 2 золотые монеты
за 5 серебряных монет получить 3 золотые и одну медную.
У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 5050 медных. На сколько уменьшилось количество серебряных монет у Николая?
Ответ: 10
Слайд 25Сколькими способами можно выложить в ряд три одинаковых красных шарика, два
Ответ: 60
Слайд 27Альпинист поднимается на гору высотой 300300 метров. Первые 5050 метров он преодолевает за 1010 минут, каждые следующие 5050 метров
Слайд 28В лотке 30 яиц: белые и рябые. Известно, что среди любых
20 яиц хотя бы одно белое. Сколько белых яиц в лотке?
Ответ: 11
Так как среди любых 12 яиц имеется хотя бы одно рябое, то белых яиц не может быть больше 11. А поскольку среди любых 20 яиц хотя бы одно белое, то рябых яиц не может быть больше 19. Так как всего в лотке 30 яиц, то единственный возможный вариант — в лотке 19 рябых яиц и 11 белых.