- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Задачи на совместную работу
Содержание
- 1. Презентация по математике на тему Задачи на совместную работу
- 2. Если вы хотите научиться плавать, то
- 3. Памятка при решении задач на работу-время работы-объем работы-производительностьОбъем работы = время работы · производительность
- 4. Слайд 4
- 5. Пример 1
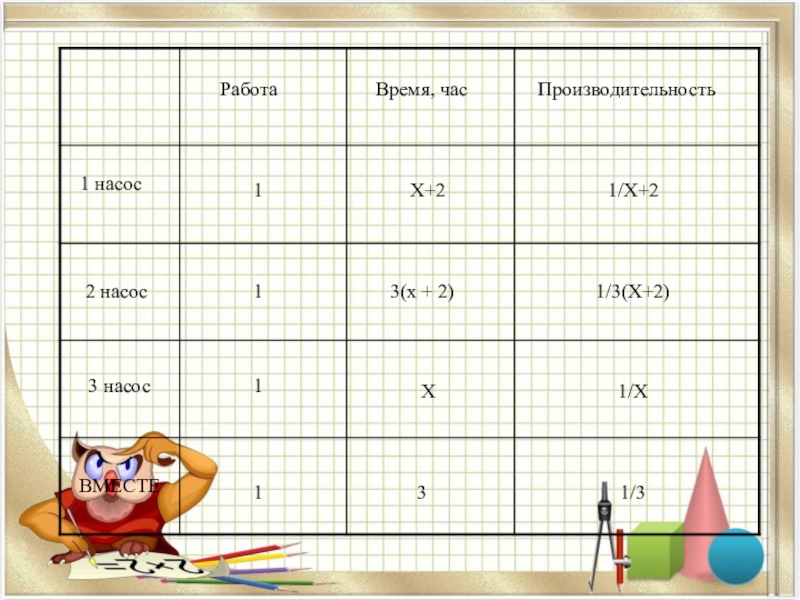
- 6. РаботаВремя, часПроизводительность1 насос2 насос3 насосВМЕСТЕ1111X+23X3(х + 2)1/X+21/3(X+2)1/31/X
- 7. Алгоритм решения задачи 1. Внесем в
- 8. Уравнение1/х+2 + 1/3(х+2) + 1/х = 1/3Решив
- 9. Реши сам!Два маляра, работая вместе, могут за
- 10. Пример 2
- 11. Пример 3Бак заполняют керосином за 2часа 30
- 12. Решение задачи Так как объём бака не
- 13. Реши сам ! Два фермера, работая
- 14. Особенности решения задач «на работу».А=Р*t, где А-работа
- 15. На изготовление 180 деталей первый рабочий тратит
- 16. Составим уравнение по условию задачи:х (х +
- 17. Бассейн наполняется двумя трубами, действующими одновременно, за
- 18. Пример 1
Слайд 1
Мастер – класс на тему: «Решение задач на совместную работу»
Учитель математики
МКОУ СШ №1
г. Фролово
Калинина Е.И.
Слайд 2Если вы хотите научиться плавать,
то смело входите в воду,
а если хотите научиться
решать задачи,
то решайте их!
(Д. Пойа)
Слайд 3Памятка при решении задач на работу
-время работы
-объем работы
-производительность
Объем работы = время
Слайд 5Пример 1
Для наполнения плавательного
Решение: Эту задачу удобно решать с помощью таблицы.
Слайд 6Работа
Время, час
Производительность
1 насос
2 насос
3 насос
ВМЕСТЕ
1
1
1
1
X+2
3
X
3(х + 2)
1/X+2
1/3(X+2)
1/3
1/X
Слайд 7Алгоритм решения задачи
1. Внесем в таблицу известные величины (
2. Одну из неизвестных величин обозначим за х.
3. Остальные неизвестные величины выразим через х, используя условие задачи или формулы.
. 4Составим уравнение.
5. Решим уравнение и ответим на главный вопрос задачи.
Слайд 8Уравнение
1/х+2 + 1/3(х+2) + 1/х = 1/3
Решив уравнение, мы найдем х=6
6ч-
Тогда время первого насоса 8ч, второго 24ч.
Значит минимальное время работы двух насосов – это время работы 1 и3 насосов ,т.е. 14ч
Определим минимальную стоимость наполнения бассейна двумя насосами.
140*14=1960(руб.)
Ответ: 1960 руб.
Слайд 9Реши сам!
Два маляра, работая вместе, могут за 1ч покрасить стену площадью
Ответ: 4ч
Слайд 11Пример 3
Бак заполняют керосином за 2часа 30 минут с помощью трех
Слайд 12Решение задачи
Так как объём бака не указан, то примем объём
Решим уравнение 1/16х = 2,5
Х =1/ 40
Производительность второго насоса равна 1/ 40 * 5 = 1/ 8
Производительность третьего насоса равна 1/ 40 * 8 = 1/ 5.
Совместная производительность второго и третьего насосов равна 1/ 8 + 1/ 5 =13/40
За 1ч 30мин второй и третий насосы наполнят 13/ 40 * 78/ 60 = 13/ 40 * 1,3 = 16,9/ 40 = 0,4225 объёма бака.
Итак, при совместной работе 2 и 3 насосов за 1ч 18 мин будет заполнено 0,4225 *100% =42,25% объёма бака.
Слайд 13Реши сам !
Два фермера, работая вместе могут вспахать поле
Ответ: 28 ч.
Слайд 14Особенности решения задач «на работу».
А=Р*t, где А-работа
t- время
Р=А/t
t=А/Р
Если в условии не дана вся работа, то её можно принять за 1
Общая производительность равна сумме производительностей.
Слайд 15На изготовление 180 деталей первый рабочий тратит на 3 часа меньше,
Решение.
Пусть х – производительность (дет./час) второго рабочего, тогда
(х+3) – производительность первого рабочего
Значит
Слайд 16Составим уравнение по условию задачи:
х (х + 3) ≠ 0
х ≠
180х + 3х² + 9х = 180х + 540
3х² + 9х – 540 = 0 | : 3
х² + 3х – 180 = 0
D = 9 - 4·(- 180) =9 + 720 = 729 = 27²
х1 = 24: 2 = 12
х2 = -30 : 2 < 0 (не подходит)
Проверка.
Ответ: производительность второго рабочего 12 деталей в час
Слайд 17Бассейн наполняется двумя трубами, действующими одновременно, за 2 часа.За сколько часов
Решение.
самостоятельно в парах.
Ответ: 3
Слайд 18Пример 1
Для наполнения плавательного
Решение: Эту задачу удобно решать с помощью таблицы.