- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Задачи по теории вероятностей (9 и 11 класс)
Содержание
- 1. Презентация по математике на тему Задачи по теории вероятностей (9 и 11 класс)
- 2. Определение вероятностиВероятностью события A называют отношение числа
- 3. Свойства вероятностиСвойство 1. Вероятность достоверного события равна
- 4. Решение.Игральные кости – это кубики с 6
- 5. В случайном эксперименте симметричную монету бросают дважды.
- 6. В чемпионате по гимнастике участвуют 20 спортсменок:
- 7. В среднем из 1000 садовых насосов, поступивших
- 8. Решение: 100 + 8 = 108 –
- 9. В соревнованиях по толканию ядра участвуют 4
- 10. Научная конференция проводится в 5 дней. Всего
- 11. Конкурс исполнителей проводится в 5 дней. Всего
- 12. На семинар приехали 3 ученых из Норвегии,
- 13. Перед началом первого тура чемпионата по бадминтону
- 14. В сборнике билетов по биологии всего 55
- 15. В сборнике билетов по математике всего 25
- 16. На чемпионате по прыжкам в воду выступают
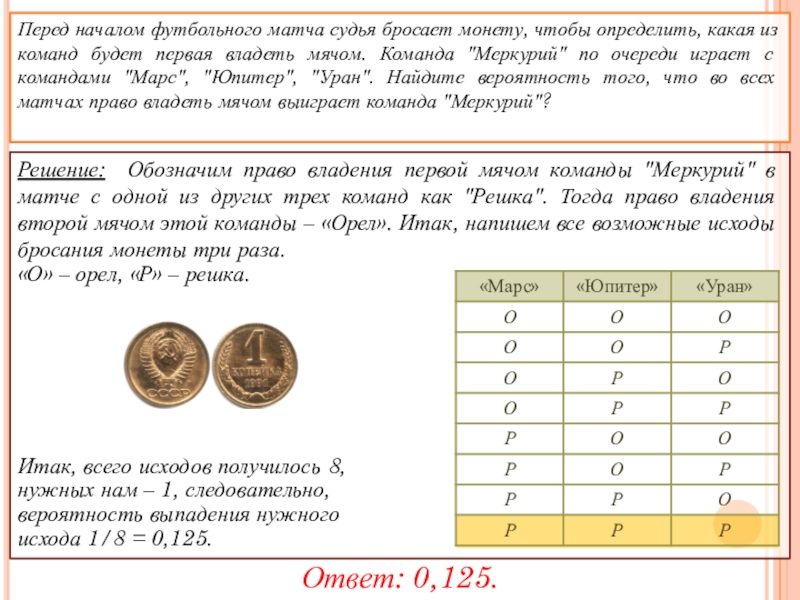
- 17. Решение: Обозначим право владения первой мячом команды
- 18. Решение.В сумме на двух кубиках должно выпасть
- 19. Решение.При условии, что у Тоши выпало 3
- 20. Решение: Всего команд 20, групп – 5.
- 21. Вася, Петя, Коля и Лёша бросили жребий –
- 22. На клавиатуре телефона 10 цифр, от 0
- 23. Решение: 10, 11, 12, 13, 14, 15,
- 24. Решение: Обозначим право владения первой мячом команды
- 25. Решение: В сумме должно выпасть 5 очков.
- 26. В случайном эксперименте симметричную монету бросают дважды.
- 27. Решение: Общее количество выступающих на фестивале групп
- 28. Решение: Из 5000 тысяч новорожденных 5000 −
- 29. Решение: В самолете 12 + 18 = 30 мест удобны пассажиру
- 30. Решение: Всего в запасную аудиторию направили 250 − 120
- 31. Решение: Пусть один из близнецов находится в
- 32. Решение: Машин желтого цвета с черными надписями
- 33. Решение: На первом рейсе 6 мест, всего
- 34. Решение: В кармане было 4 конфеты, а
Слайд 2Определение вероятности
Вероятностью события A называют отношение числа m благоприятствующих этому событию
Пусть k – количество бросков монеты, тогда количество всевозможных исходов: n = 2k.
Пусть k – количество бросков кубика, тогда количество всевозможных исходов: n = 6k.
Слайд 3Свойства вероятности
Свойство 1. Вероятность достоверного события равна единице: Р(А) = 1.
Свойство
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей: 0 ≤ Р(А) ≤ 1.
Слайд 4Решение.
Игральные кости – это кубики с 6 гранями. На первом кубике
Т.е. всего различных вариантов 6×6 = 36.
Варианты (исходы эксперимента) будут такие:
1; 1 1; 2 1; 3 1; 4 1; 5 1; 6
2; 1 2; 2 2; 3 2; 4 2; 5 2; 6
и т.д. ..............................
6; 1 6; 2 6; 3 6; 4 6; 5 6; 6
Подсчитаем количество исходов (вариантов), в которых сумма очков двух кубиков равна 8.
2; 6 3; 5; 4; 4 5; 3 6; 2.
Всего 5 вариантов.
Найдем вероятность: 5/36 = 0,138 ≈ 0,14.
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Ответ: 0,14.
Слайд 5В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что
Решение.
Всего 4 варианта: о; о о; р р; р р; о.
Благоприятных 2: о; р и р; о.
Вероятность равна 2/4 = 1/2 = 0,5.
Ответ: 0,5.
Слайд 6В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7
Решение.
Всего участвует 20 спортсменок,
из которых 20 – 8 – 7 = 5 спортсменок из Китая.
Вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна 5/20 = 1/4 = 0,25.
Ответ: 0,25.
Слайд 7В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают.
Решение:
1000 – 5 = 995 – насосов не подтекают.
Вероятность того, что один случайно выбранный для контроля насос не подтекает, равна
995/1000 = 0,995.
Ответ: 0,995.
Слайд 8Решение:
100 + 8 = 108 – сумок всего (качественных и
Вероятность того, что купленная сумка окажется качественной, равна 100/108 = 0,(925) ≈ 0,93.
Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Ответ: 0,93.
Слайд 9В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7
Ответ: 0,36.
Решение:
Всего участвует 4 + 7 + 9 + 5 = 25 спортсменов. Вероятность того, что спортсмен, который выступает последним, окажется из Швеции, равна
9/25 = 36/100 = 0,36.
Слайд 10Научная конференция проводится в 5 дней. Всего запланировано 75 докладов − первые
Ответ: 0,16.
Решение:
В последний день конференции запланировано
(75 – 17 × 3) : 2 = 12 докладов.
Вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 12/75 = 4/25 = 0,16.
Слайд 11Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений − по одному
Ответ: 0,225.
285923
Решение:
В третий день конкурса запланировано
(80 – 8) : 4 = 18 выступлений.
Вероятность того, что выступление представителя России состоится в третий день конкурса, равна
18/80 = 9/40 = 225/1000 = 0,225.
Слайд 12На семинар приехали 3 ученых из Норвегии, 3 из России и
Ответ: 0,3.
Решение:
Всего участвует 3 + 3 + 4 = 10 ученых.
Вероятность того, что восьмым окажется доклад ученого из России, равна 3/10 = 0,3.
Слайд 13Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые
Ответ: 0,36.
Решение:
Нужно учесть, что Руслан Орлов должен играть с каким-либо бадминтонистом из России. И сам Руслан Орлов тоже из России.
Вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна 9/25 = 36/100 = 0,36.
Слайд 14В сборнике билетов по биологии всего 55 билетов, в 11 из
Ответ: 0,2.
Решение:
Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике, равна 11/55 =1/5 = 0,2.
Слайд 15В сборнике билетов по математике всего 25 билетов, в 10 из
Ответ: 0,6.
Решение:
25 – 10 = 15 – билетов не содержат вопрос по неравенствам.
Вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна
15/25 = 3/5 = 0,6.
Слайд 16На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них
Ответ: 0,36.
285928
Решение:
Всего участвует 25 спортсменов.
Вероятность того, что шестым будет выступать прыгун из Парагвая, равна 9/25 = 36/100 = 0,36.
Слайд 17Решение: Обозначим право владения первой мячом команды "Меркурий" в матче с
«О» – орел, «Р» – решка.
Итак, всего исходов получилось 8,
нужных нам – 1, следовательно,
вероятность выпадения нужного
исхода 1/8 = 0,125.
Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд будет первая владеть мячом. Команда "Меркурий" по очереди играет с командами "Марс", "Юпитер", "Уран". Найдите вероятность того, что во всех матчах право владеть мячом выиграет команда "Меркурий"?
Ответ: 0,125.
Слайд 18Решение.
В сумме на двух кубиках должно выпасть 8 очков. Это возможно,
2 и 6
6 и 2
3 и 5
5 и 3
4 и 4
Всего 5 вариантов. Подсчитаем количество исходов (вариантов), в которых при первом броске выпало 2 очка.
Такой вариант 1.
Найдем вероятность: 1/5 = 0,2.
Даша дважды бросает игральный кубик. В сумме у нее выпало 8 очков. Найдите вероятность того, что при первом броске выпало 2 очка.
Ответ: 0,2.
Слайд 19Решение.
При условии, что у Тоши выпало 3 очка, возможны следующие варианты:
3
3 и 2
3 и 3
3 и 4
3 и 5
3 и 6
Всего 6 вариантов. Подсчитаем количество исходов, в которых Гоша не выиграет, т.е. наберет 1, 2 или 3 очка.
Таких вариантов 3.
Найдем вероятность: 3/6 = 0,5.
Тоша и Гоша играют в кости. Они бросают кубик по одному разу. Выигрывает тот, кто выбросил больше очков. Если очков выпало поровну, то наступает ничья. Первым бросил Тоша, у него выпало 3 очка. Найдите вероятность того, что Гоша не выиграет.
Ответ: 0,5.
Слайд 20Решение:
Всего команд 20, групп – 5.
В каждой группе –
Итак, всего исходов получилось 20, нужных нам – 4, значит, вероятность выпадения нужного исхода 4/20 = 0,2.
В чемпионате мира участвует 20 команд. С помощью жребия их нужно разделить на пять групп по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется в третьей группе.
Ответ: 0,2.
Слайд 21Вася, Петя, Коля и Лёша бросили жребий – кому начинать игру. Найдите
Ответ: 0,25.
Решение:
Вероятность того, что игру должен будет начинать любой из мальчиков равна
1/4 = 0,25.
В том числе и для Пети.
Слайд 22На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность
Ответ: 0,5.
Решение:
Количество четных цифр на клавиатуре равно 5:
0, 2, 4, 6, 8
всего же цифр на клавиатуре 10, тогда вероятность что случайно нажатая цифра будет чётной равна
5/10 = 0,5.
Слайд 23Решение:
10, 11, 12, 13, 14, 15, 16, 17, 18, 19
Р
Ответ: 0,3.
Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?
Слайд 24Решение: Обозначим право владения первой мячом команды «Физик" в матче с
«О» – орел, «Р» – решка.
Итак, всего исходов получилось 23 = 8, нужных нам – 3,
следовательно, вероятность выпадения нужного исхода равна:
3/8 = 0,375.
Ответ: 0,375.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
Слайд 25Решение:
В сумме должно выпасть 5 очков. Это возможно, если будут
1 и 4
4 и 1
2 и 3
3 и 2
Всего 4 варианта.
Ответ: 4.
Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «А = сумма очков равна 5»?
Слайд 26В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что
Решение.
Всего 4 варианта: о; о о; р р; р р; о.
Благоприятных 1: о; р.
Вероятность равна 1/4 = 0,25.
Ответ: 0,25.
Слайд 27Решение:
Общее количество выступающих на фестивале групп для ответа на вопрос
Д − Ш − Н
Д − Н − Ш
Ш − Н − Д
Ш − Д − Н
Н − Д − Ш
Н − Ш − Д
Дания находится после Швеции и Норвегии в двух случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна
Р = 2/6 = 1/3 ≈ 0,33
Ответ: 0,33.
На рок-фестивале выступают группы – по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
Слайд 28Решение:
Из 5000 тысяч новорожденных 5000 − 2512 = 2488 девочек.
2488/5000 = 0,4976 ≈ 0,498
В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных.
Ответ: 0,498.
Слайд 29Решение:
В самолете 12 + 18 = 30 мест удобны пассажиру В., а всего в
P = 30 : 300 = 0,1.
На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.
Ответ: 0,1.
Слайд 30Решение:
Всего в запасную аудиторию направили
250 − 120 − 120 = 10 человек.
Поэтому вероятность
P = 10 : 250 = 0,04.
На олимпиаде в вузе участников рассаживают по трём аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 250 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Ответ: 0,04.
Слайд 31Решение:
Пусть один из близнецов находится в некоторой группе.
Вместе с
Вероятность того, что второй близнец окажется среди этих 12 человек, равна
P = 12 : 25 = 0,48.
В классе 26 человек, среди них два близнеца – Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
Ответ: 0,48.
Слайд 32Решение:
Машин желтого цвета с черными надписями 23, всего машин 50.
P = 23 : 50 = 0,46.
В фирме такси в наличии 50 легковых автомобилей; 27 из них чёрные с жёлтыми надписями на бортах, остальные – жёлтые с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
Ответ: 0,46.
Слайд 33Решение:
На первом рейсе 6 мест, всего мест 30. Тогда вероятность
P = 6 : 30 = 0,2.
В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
Ответ: 0,2.
Слайд 34Решение:
В кармане было 4 конфеты, а выпала одна конфета. Поэтому
В кармане у Миши было четыре конфеты – «Грильяж», «Белочка», «Коровка» и «Ласточка», а так же ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».
Ответ: 0,25.