школа №111 Советского района Волгограда
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Все об иррациональности
Содержание
- 1. Презентация по математике на тему Все об иррациональности
- 2. Иррациональные выражения – это выражения, которые имеют корень.
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
- 6. Слайд 6
- 7. Слайд 7
- 8. Слайд 8
- 9. Слайд 9
- 10. При вычислении таких выражений необходимо обратить внимание
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Под упрощением иррациональных алгебраических выражений понимается приведение
- 22. Теперь изначальное выражение имеет вид: Приведём её
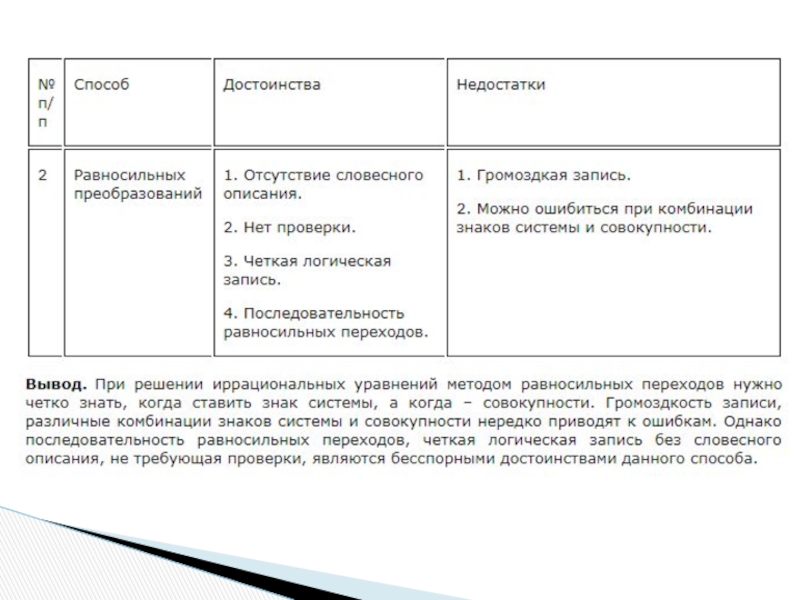
- 23. Правила решения иррациональных уравнений
- 24. Первый способ: возведение обеих частей уравнения в
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Слайд 33
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. https://xn--j1ahfl.xn--p1ai/library/metodi_resheniya_irratcionalnih_uravnenij_102827.htmlhttps://multiurok.ru/files/issliedovatiel-skaia-rabota-214.htmlhttps://scienceforum.ru/2018/article/2018003965http://xn--i1abbnckbmcl9fb.xn--p1ai/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/517610/https://www.yaklass.ru/p/algebra/11-klass/stepeni-i-korni-stepennye-funktcii-11016/funktciia-kornia-n-i-stepeni-11554/re-d8c8d8a1-ebc0-480c-9c68-90fa5aa0dae1https://www.yaklass.ru/p/algebra/11-klass/stepeni-i-korni-stepennye-funktcii-11016/funktciia-kornia-n-i-stepeni-11554/re-b320b728-f779-4868-932b-7008af86588chttp://www.cleverstudents.ru/functions/elementary_functions_classification.htmlЛитература
Иррациональные выражения – это выражения, которые имеют корень. То есть это выражения, имеющие радикалы.Что такое иррациональные выражения?
Слайд 1«Все об иррациональности»
Учитель: Дурникина
Надежда Ивановна
Муниципальное общеобразовательное учреждение «Средняя
Слайд 2Иррациональные выражения – это выражения, которые имеют корень. То есть это выражения,
имеющие радикалы.
Что такое иррациональные выражения?
Слайд 10При вычислении таких выражений необходимо обратить внимание на ОДЗ. Часто они
требуют дополнительных преобразований в виде раскрытия скобок, приведения подобных, группировок и так далее. Основа таких преобразований – действия с числами. Преобразования иррациональных выражений придерживаются строгого порядка.
Основные виды преобразований иррациональных выражений
Слайд 21Под упрощением иррациональных алгебраических выражений понимается приведение его к виду, содержащему
меньшее число алгебраических операций. Зачастую, это достигается разложением исходного выражения на множители и вынесением общего множителя за скобки.
Пример:
Для начала представим числитель первой дроби в виде:
Множитель является общим для числителя и знаменателя. Проводим сокращение.
Пример:
Для начала представим числитель первой дроби в виде:
Множитель является общим для числителя и знаменателя. Проводим сокращение.
Упрощение иррациональных алгебраических выражений
Слайд 22
Теперь изначальное выражение имеет вид:
Приведём её к общему знаменателю
, для этого числитель
и знаменатель второй дроби помножим на , теперь эта
дробь имеет вид:
и знаменатель второй дроби помножим на , теперь эта
дробь имеет вид:
Слайд 24Первый способ: возведение обеих частей уравнения в одну и ту же
степень с после
дующей проверкой.
дующей проверкой.
Методы решения иррациональных уравнений
Слайд 37https://xn--j1ahfl.xn--p1ai/library/metodi_resheniya_irratcionalnih_uravnen
ij_102827.html
https://multiurok.ru/files/issliedovatiel-skaia-rabota-214.html
https://scienceforum.ru/2018/article/2018003965
http://xn--i1abbnckbmcl9fb.xn--p1ai/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/517610/
https://www.yaklass.ru/p/algebra/11-klass/stepeni-i-korni-stepennye-funktcii-11016/funktciia-kornia-n-i-stepeni-11554/re-d8c8d8a1-ebc0-480c-9c68-90fa5aa0dae1
https://www.yaklass.ru/p/algebra/11-klass/stepeni-i-korni-stepennye-funktcii-11016/funktciia-kornia-n-i-stepeni-11554/re-b320b728-f779-4868-932b-7008af86588c
http://www.cleverstudents.ru/functions/elementary_functions_classification.html
Литература
