- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Уравнения, тождества и неравенства при решении геометрических задач
Содержание
- 1. Презентация по математике на тему Уравнения, тождества и неравенства при решении геометрических задач
- 2. Содержание.Задачи на отыскание наибольших и наименьших величин.Задачи
- 3. Первый раздел. Задача №1Из всех прямоугольных треугольников
- 4. Задача №2В данный полукруг вписать прямоугольник наибольшей
- 5. Второй раздел. Задача №3Дано: S- площадь p- полупериметрДоказать: Решение:Ответ:
- 6. Задача №4(ЗФТШ)Стороны треугольник a, b и c.
- 7. Задача №5Доказать, что катеты a и b
- 8. Третий раздел. Задача №6Определить угол при основание
- 9. Задача №6Определить угол при основание равнобедренного треугольника,
- 10. Время вопросов
- 11. Спасибо за внимание
Слайд 2Содержание.
Задачи на отыскание наибольших и наименьших величин.
Задачи на геометрические
Задачи, решаемые с помощью тригонометрических функций
Слайд 3Первый раздел.
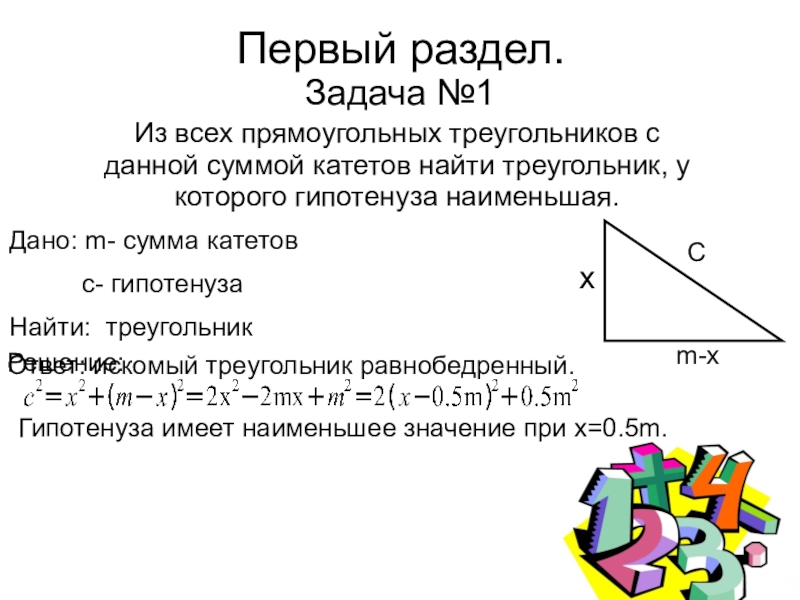
Задача №1
Из всех прямоугольных треугольников с данной суммой катетов найти
Дано: m- сумма катетов
c- гипотенуза
Найти: треугольник
x
C
m-x
Решение:
Гипотенуза имеет наименьшее значение при x=0.5m.
Ответ: искомый треугольник равнобедренный.
Слайд 4Задача №2
В данный полукруг вписать прямоугольник наибольшей площади.
Дано: O- центр полукруга
ABCD- вписанный прямоугольник, наибольшей площади
Ответ: если данный угол равен 45° , то вписанный прямоугольник имеет наибольшую площадь.
-наибольшее
Слайд 6
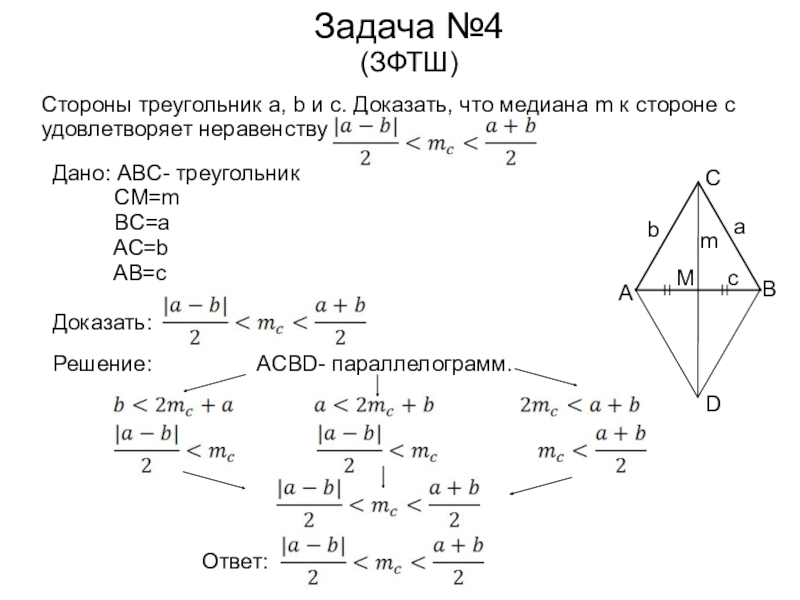
Задача №4
(ЗФТШ)
Стороны треугольник a, b и c. Доказать, что медиана m
Дано: ABC- треугольник
CM=m
BC=a
AC=b
AB=c
Доказать:
Решение: ACBD- параллелограмм.
Слайд 7Задача №5
Доказать, что катеты a и b прямоугольного треугольника и гипотенуза
б)
Дано: ABC- прямоугольный треугольник
a,b- катеты треугольника
c- гипотенуза треугольника
h- высота, проведенная к гипотенузе
Решение:
Ответ:
Ответ:
а)
б)
Доказать: а)
б)
Слайд 8
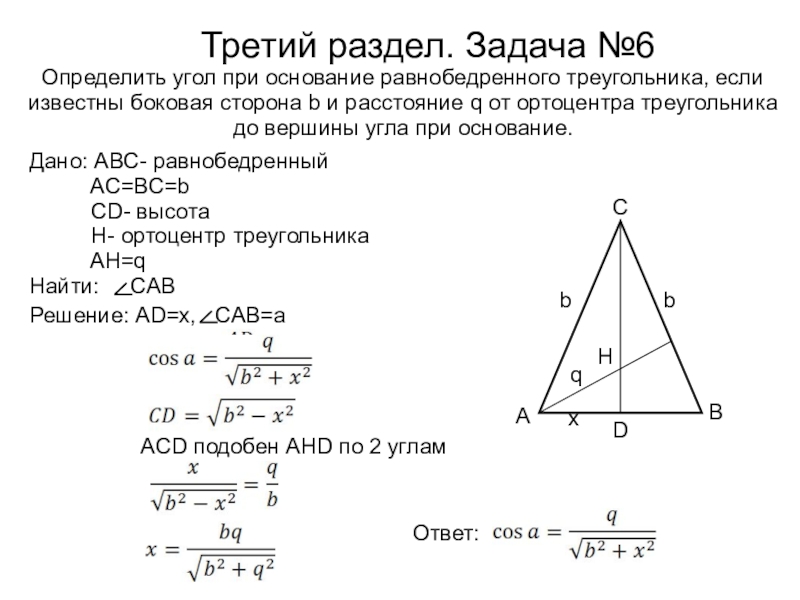
Третий раздел. Задача №6
Определить угол при основание равнобедренного треугольника, если известны
Ответ:
ACD подобен AHD по 2 углам
Слайд 9
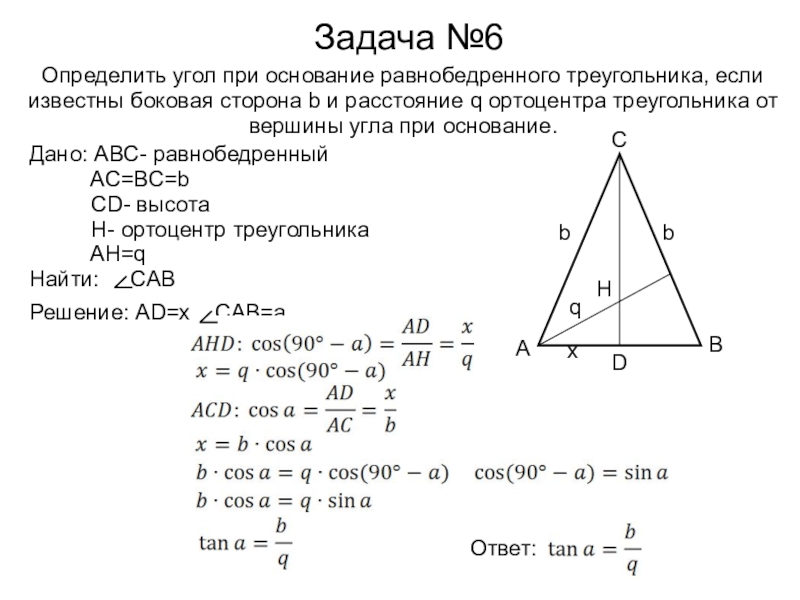
Задача №6
Определить угол при основание равнобедренного треугольника, если известны боковая сторона
Решение: AD=x, CAB=a
Ответ: