- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Тригонометрия в реальной жизни
Содержание
- 1. Презентация по математике на тему Тригонометрия в реальной жизни
- 2. Тригонометрия в окружающем нас миреРаботу выполнил: учитель математики Вансович Н.В..
- 3. ВведениеТригонометрия - это раздел математики, изучающий тригонометрические
- 4. ИсторияТригонометрия– (от греч. Trigwnon-треугольник и metrew- измеряю)По
- 5. Арабские ЗиджиУлугбек (1394-1449) -основатель научной школы вСамарканде.Первые трактаты о плоской тригонометрии (X—XI вв.).
- 6. Древняя Греция Потребность в решении
- 7. Древняя Греция Вместо таблиц этих
- 8. Индия Значительные высоты достигла тригонометрия и
- 9. ИндияИндийцы также знали: Формулы для кратких углов
- 10. Южноиндийские математики в 16 веке добились больших
- 11. Европа Ряды для синуса и
- 12. Дальнейшее развитие тригонометрия получила
- 13. Россия Современные обозначения синуса и
- 14. Значимые люди в тригонометрииГиппарх Никейский ( 180
- 15. Построил таблицы тангенсов, котангенсов и косекансов
- 16. Насир-эд-Дин из Туса(1201 – 1274 г. н.э)
- 17. Франсуа Виет (1540 – 1603 г.)Исаак Ньютон
- 18. Леонард Эйлер (1707 – 1783 г.
- 19. Тригонометрия в искусстве cos2 С +
- 20. Тригонометрия в физике Колебания, при
- 21. Слайд 21
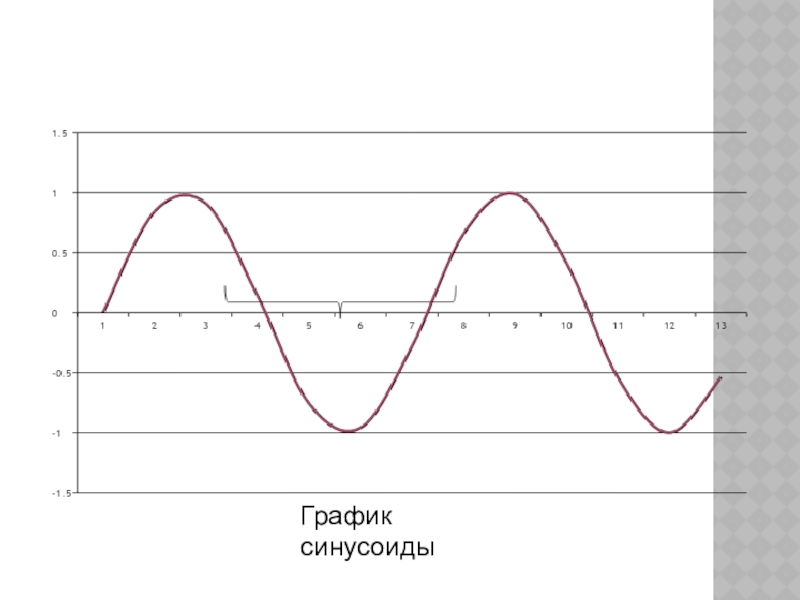
- 22. График синусоиды
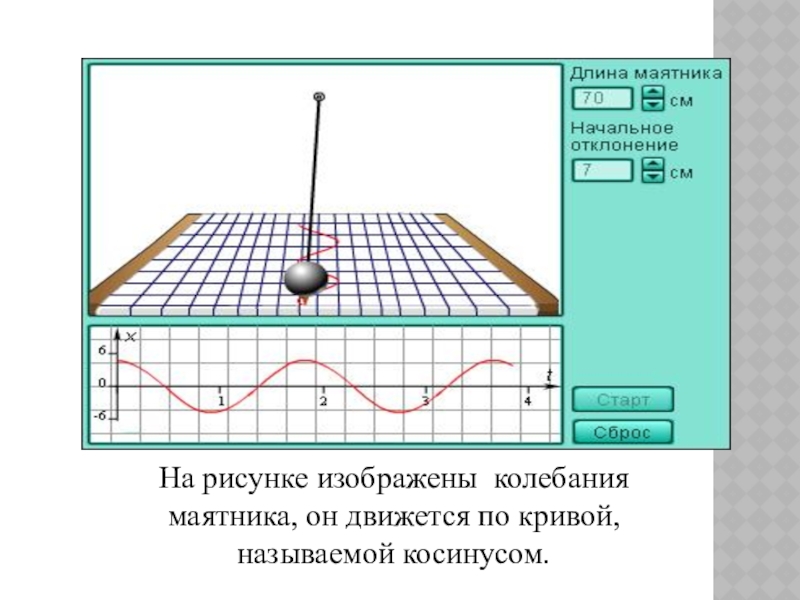
- 23. На рисунке изображены колебания маятника, он движется по кривой, называемой косинусом.
- 24. Слайд 24
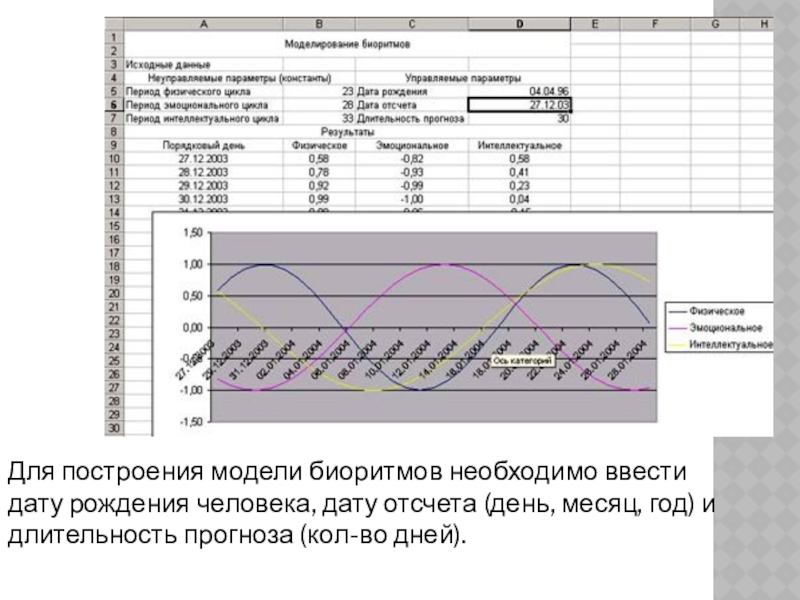
- 25. Для построения модели биоритмов необходимо ввести
- 26. Американские ученые утверждают, что мозг оценивает расстояние
- 27. Движение рыб в воде происходит
- 28. Тригонометрия в архитектуре Детская школа Гауди в барселоне
- 29. Сантьяго Калатрава Винодельня «Бодегас Исиос»
- 30. Феликс Кандела Ресторан в Лос-Манантиалесе
- 31. Тригонометрия в музыке Согласно дошедшим из древности
- 32. Тетраэдр из различных типов аккордов четырех звуков:синий
- 33. Теория радуги Радуга возникает из-за
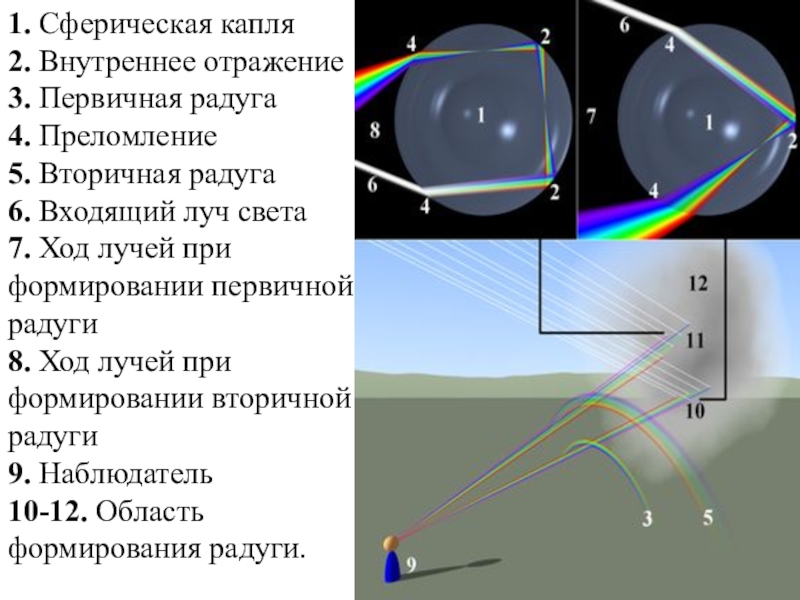
- 34. 1. Сферическая капля 2. Внутреннее отражение 3.
- 35. Северное сияние Проникновение в верхние
- 36. Спасибо за внимание!
Слайд 1«Теория без практики мертва или бесполезна, практика без теории невозможна или
Слайд 3Введение
Тригонометрия - это раздел математики, изучающий тригонометрические функции. Сложно представить, но
Слайд 4История
Тригонометрия– (от греч. Trigwnon-треугольник и metrew- измеряю)
По звездам вычисляли
местонахождение корабля в
море.
Древние люди вычисляли
высоту дерева,
сравнивая длину его тени с
длиной тени от шеста,
высота которого была известна.
Слайд 5Арабские Зиджи
Улугбек (1394-1449) -
основатель научной школы в
Самарканде.
Первые трактаты о плоской
тригонометрии
Слайд 6Древняя Греция
Потребность в решении треугольников раньше всего возникла
Греческие астрономы не знали синусов, косинусов и тангенсов.
Слайд 7Древняя Греция
Вместо таблиц этих величин они употребляли таблицы:
Слайд 8Индия
Значительные высоты достигла тригонометрия и у индийских
средневековых астрономов.
Главным
Замена хорд синусами, что позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника.
Таким образом в Индии было положено начало тригонометрии как учению о тригонометрических величинах. Индийские ученые пользовались различными тригонометрическими соотношениями, в том числе и теми, которые используются в современной науке.
Слайд 9Индия
Индийцы также знали:
Формулы для кратких углов sin na , cos
Первая таблица синусов «Сурья-сиддханте» у Ариабхаты. Она приведена через 3,45.
Позднее ученые составили более подробные таблицы: например Бхаскара приводит таблицу синусов через 1 .
Слайд 10Южноиндийские математики в 16 веке добились больших успехов в области суммирования
Индия
Слайд 11Европа
Ряды для синуса и косинуса вывел И.Ньютон в
Ряд арктангенса найден Дж.Грегори в 1671 г. И Г.В.Лейбницем в 1673 г.
Теорему тангенсов доказал Региомонтан (латинизированное имя немецкого астронома и математика Иоганна Мюллера (1436-1476)). Региомонтан составил также подробные тригонометрические таблицы;
Слайд 12 Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов
Европа
Слайд 13Россия
Современные обозначения синуса и косинуса знаками sin x
Кроме того, Эйлер вводит следующие сокращенные обозначения тригонометрических функций угла x: tang x, cos x, sin x, cotg x.
Далее Эйлер установил связь тригонометрических функций с показательными и дал правило для определения знаков функций в различных четвертях круга.
Слайд 14Значимые люди в тригонометрии
Гиппарх Никейский
( 180 – 125 г. до
Таблица числовых значений хорд
Таблица для определения соотношений между элементами треугольников
Первая таблица синусов, высчитанная по хордам в окружности
«Альмагест – самая значимая тригонометрическая работа всей античности
Клавдий Птолемей (90 – 168 г н.э)
Слайд 15 Построил таблицы тангенсов, котангенсов и косекансов
Присоединил к линиям синусов
Установил основные соотношения между этими линиями
Дал определения функциям
Установил формулу двойного угла
Ал-Батани
( ок. 900 г. н.э)
Абу-ль-Вефа
( 940 – 997 г. н.э)
Слайд 16Насир-эд-Дин из Туса
(1201 – 1274 г. н.э)
Ал-Хорези
(783 –
Автор трактата о полном четырехстороннике
Построил таблицы синусов и котангенсов
Слайд 17Франсуа Виет (1540 – 1603 г.)
Исаак Ньютон
(1643 – 1727г.)
Дополнил
Открыл «плоскую» теорему косинусов и формулы тригонометрических функций от кратных углов
Разложил функции в ряды и открыл путь для их использования в математическом анализе
Слайд 18Леонард Эйлер
(1707 – 1783 г. н.э)
Ввел понятие функции и
Разъяснил вопрос о знаках всех тригонометрических функций любого аргумента
Ричард Саусвелл
(1888-1970)
Разработал метод проектирования сложных форм в 1920 году;
Выразил тригонометрические функции как отношение координат x, y, z к длине элемента.
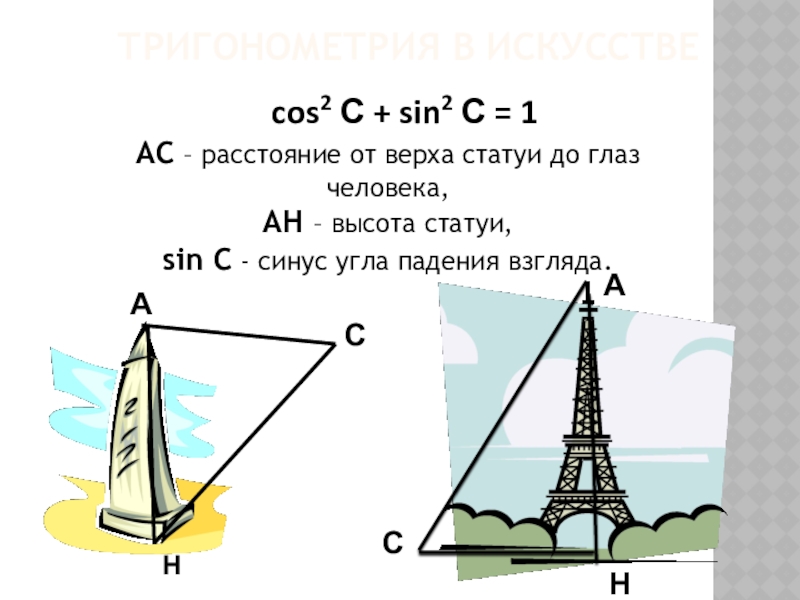
Слайд 19Тригонометрия в искусстве
cos2 С + sin2 С = 1
АС –
АН – высота статуи,
sin С - синус угла падения взгляда.
А
С
Н
А
С
Н
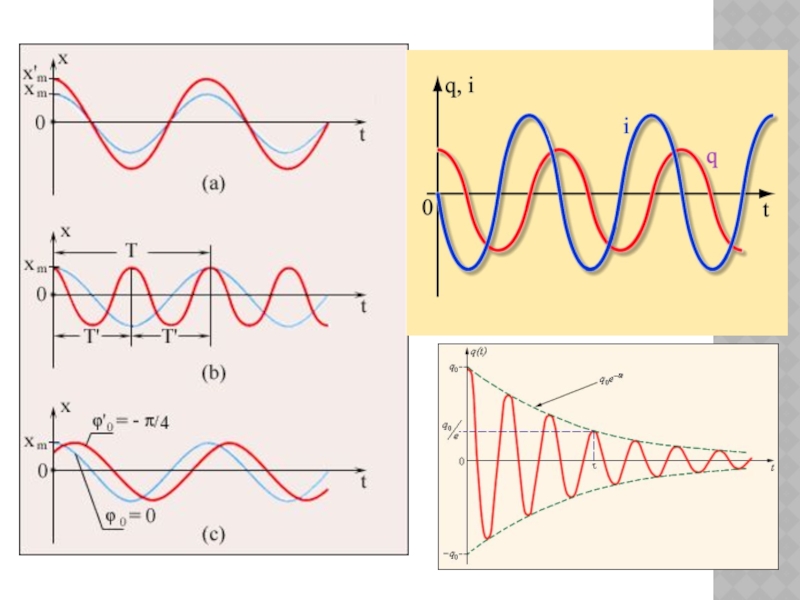
Слайд 20Тригонометрия в физике
Колебания, при которых изменения физических величин
Выражение, стоящее под знаком косинуса или синуса, называется фазой колебания:
Слайд 24
Тригонометрия и тригонометрические функции в медицине и биологии.
Одно
Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.
Основной земной ритм – суточный.
Модель биоритмов можно построить с помощью тригонометрических функций.
Слайд 25Для построения модели биоритмов необходимо ввести
Слайд 26Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол
К тому же в биологии используется такое понятие как синус сонный, синус каротидный и венозный или пещеристый синус.
Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца - комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
Слайд 27 Движение рыб в воде происходит по закону
При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
Слайд 31Тригонометрия в музыке
Согласно дошедшим из древности преданиям, первыми, кто попытался сделать
Частоты, соответствующие
одной и той же ноте в первой, второй и т.д. октавах, относятся, как 1:2:4:8…
диатоническая гамма 2:3:5
Слайд 32Тетраэдр из различных типов аккордов четырех звуков:
синий – малые интервалы;
более теплые
Слайд 33Теория радуги
Радуга возникает из-за того, что солнечный свет
n1 - показатель преломления первой среды n2 - показатель преломления второй среды
α-угол падения, β-угол преломления света
sin α / sin β = n1 / n2
Слайд 341. Сферическая капля
2. Внутреннее отражение 3. Первичная радуга
Слайд 35Северное сияние
Проникновение в верхние слои атмосферы планет заряженных
Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы.