- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теоремы Чевы и Менелая
Содержание
- 1. Презентация по математике на тему Теоремы Чевы и Менелая
- 2. AC1CB1BA1Теорема Чевы: Пусть в треугольнике АВС на
- 3. Теорема Менелая: Пусть в треугольнике АВС на
- 4. Точка С1 делит сторону АВ треугольника АВС
- 5. Задача 2В треугольнике АВС АD – медиана,
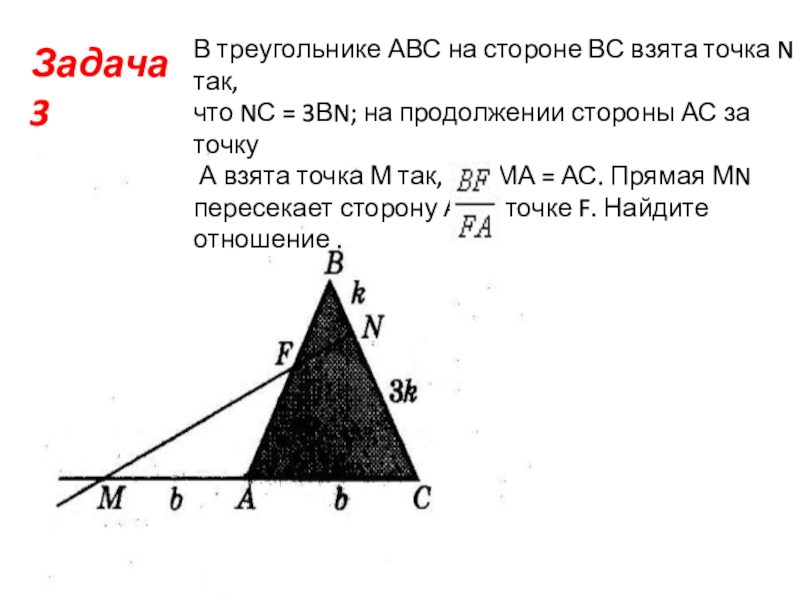
- 6. Задача 3В треугольнике АВС на стороне ВС
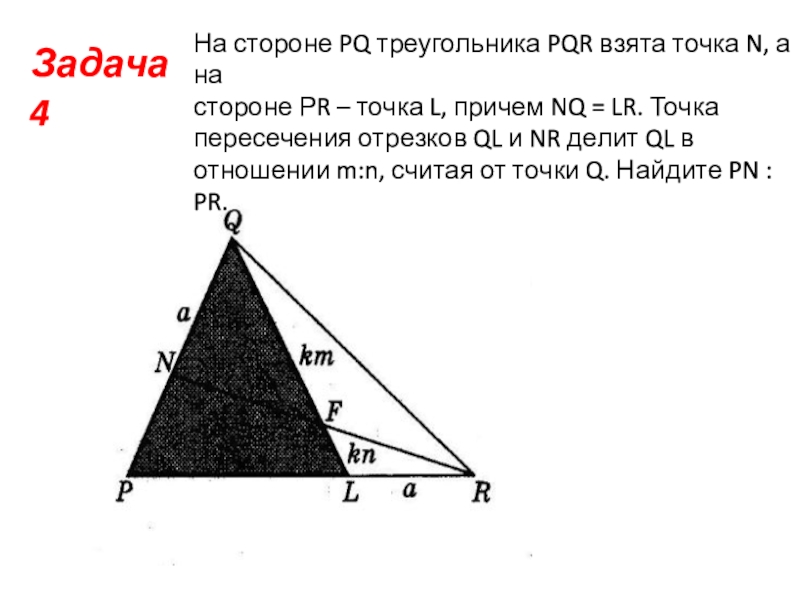
- 7. Задача 4На стороне PQ треугольника PQR взята
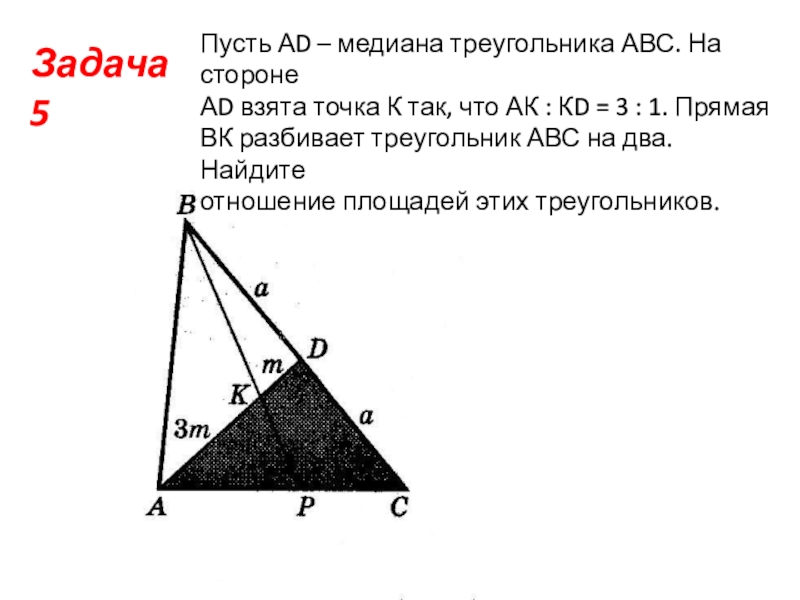
- 8. Задача 5Пусть АD – медиана треугольника АВС.
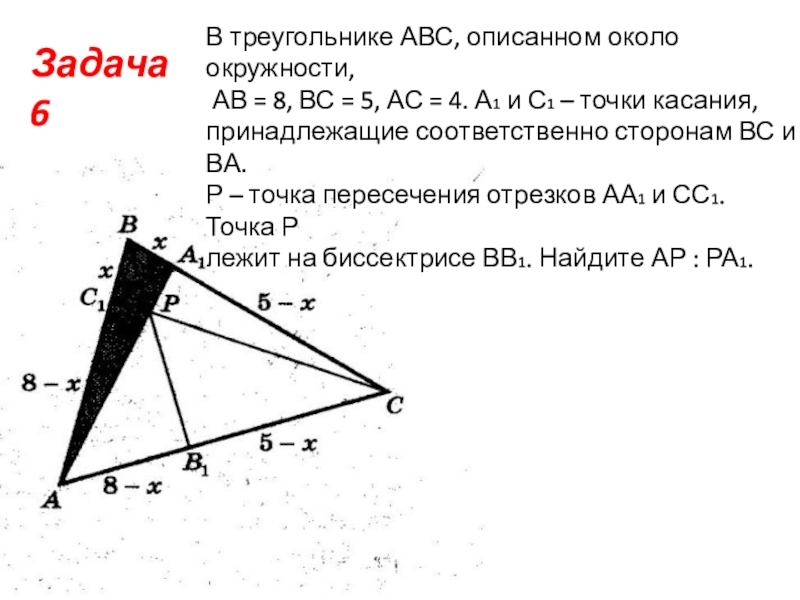
- 9. Задача 6В треугольнике АВС, описанном около окружности,
- 10. Задача 7Стороны треугольника 5, 6 и 7.
- 11. Задача 8Биссектрисы ВЕ и АD треугольника АВС
- 12. 1. На продолжениях сторон АВ, ВС, АС
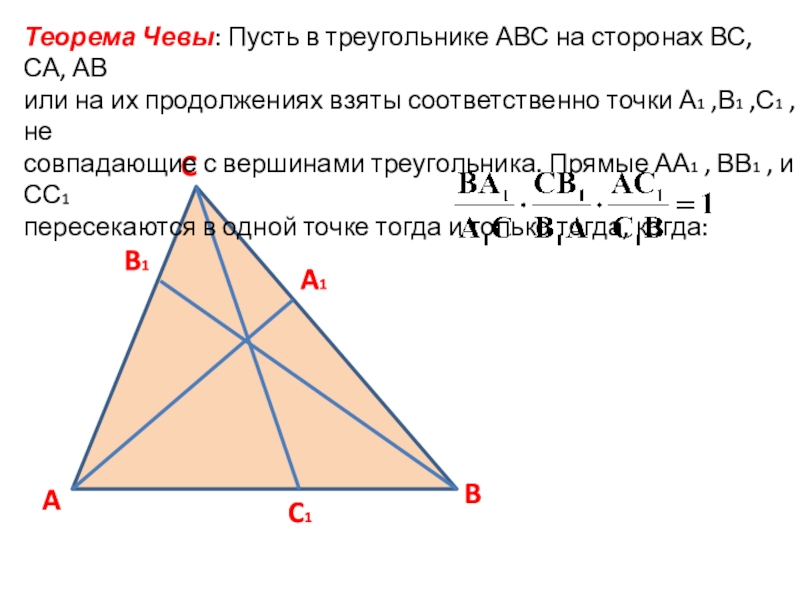
AC1CB1BA1Теорема Чевы: Пусть в треугольнике АВС на сторонах ВС, СА, АВ или на их продолжениях взяты соответственно точки А1 ,В1 ,С1 , несовпадающие с вершинами треугольника. Прямые АА1 , ВВ1 , и СС1 пересекаются в одной
Слайд 2A
C1
C
B1
B
A1
Теорема Чевы: Пусть в треугольнике АВС на сторонах ВС, СА, АВ
или на их продолжениях взяты соответственно точки А1 ,В1 ,С1 , не
совпадающие с вершинами треугольника. Прямые АА1 , ВВ1 , и СС1
пересекаются в одной точке тогда и только тогда, когда:
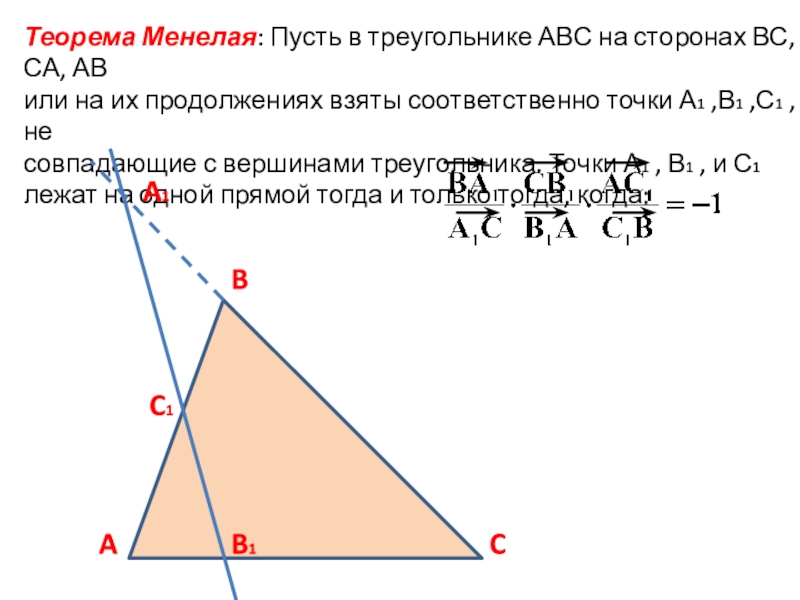
Слайд 3Теорема Менелая: Пусть в треугольнике АВС на сторонах ВС, СА, АВ
или на их продолжениях взяты соответственно точки А1 ,В1 ,С1 , не
совпадающие с вершинами треугольника. Точки А1 , В1 , и С1
лежат на одной прямой тогда и только тогда, когда:
A
B1
C
B
A1
C1
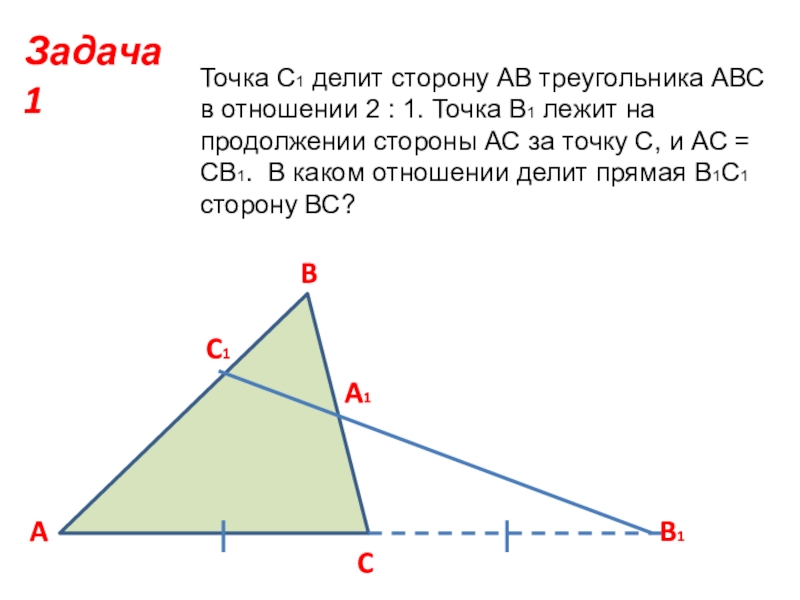
Слайд 4Точка С1 делит сторону АВ треугольника АВС в отношении 2 :
1. Точка В1 лежит на продолжении стороны АС за точку С, и АС = СВ1. В каком отношении делит прямая В1С1
сторону ВС?
сторону ВС?
Задача 1
A
B
C
C1
B1
A1
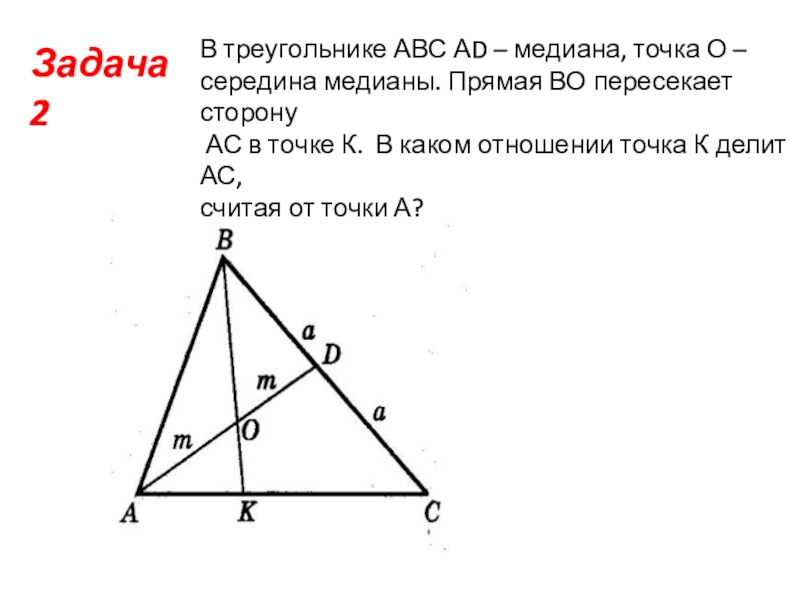
Слайд 5Задача 2
В треугольнике АВС АD – медиана, точка О –
середина
медианы. Прямая ВО пересекает сторону
АС в точке К. В каком отношении точка К делит АС,
считая от точки А?
АС в точке К. В каком отношении точка К делит АС,
считая от точки А?
Слайд 6Задача 3
В треугольнике АВС на стороне ВС взята точка N так,
что NС = 3ВN; на продолжении стороны АС за точку
А взята точка М так, что МА = АС. Прямая МN
пересекает сторону АВ в точке F. Найдите отношение .
Слайд 7Задача 4
На стороне PQ треугольника PQR взята точка N, а на
стороне РR – точка L, причем NQ = LR. Точка
пересечения отрезков QL и NR делит QL в
отношении m:n, считая от точки Q. Найдите PN : PR.
Слайд 8Задача 5
Пусть АD – медиана треугольника АВС. На стороне
АD взята
точка К так, что АК : КD = 3 : 1. Прямая
ВК разбивает треугольник АВС на два. Найдите
отношение площадей этих треугольников.
ВК разбивает треугольник АВС на два. Найдите
отношение площадей этих треугольников.
Слайд 9Задача 6
В треугольнике АВС, описанном около окружности,
АВ = 8, ВС
= 5, АС = 4. А1 и С1 – точки касания,
принадлежащие соответственно сторонам ВС и ВА.
Р – точка пересечения отрезков АА1 и СС1. Точка Р
лежит на биссектрисе ВВ1. Найдите АР : РА1.
принадлежащие соответственно сторонам ВС и ВА.
Р – точка пересечения отрезков АА1 и СС1. Точка Р
лежит на биссектрисе ВВ1. Найдите АР : РА1.
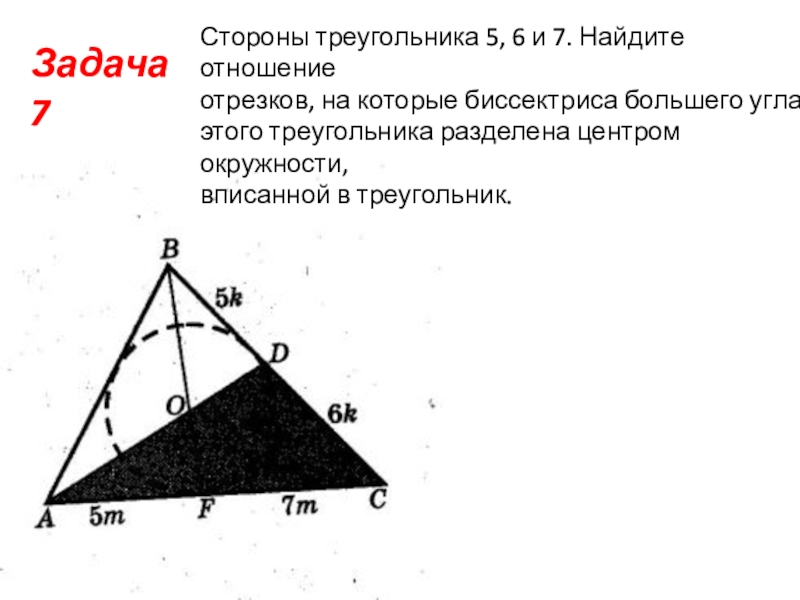
Слайд 10Задача 7
Стороны треугольника 5, 6 и 7. Найдите отношение
отрезков, на
которые биссектриса большего угла
этого треугольника разделена центром окружности,
вписанной в треугольник.
этого треугольника разделена центром окружности,
вписанной в треугольник.
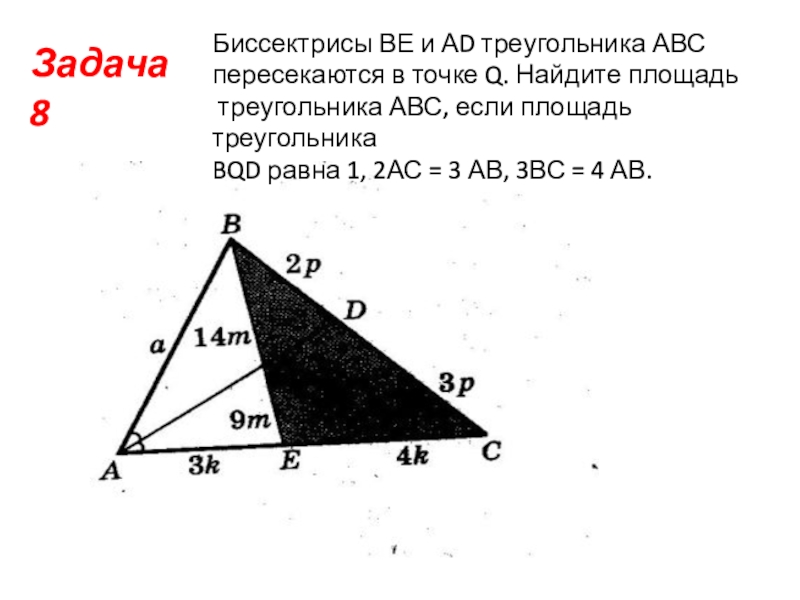
Слайд 11Задача 8
Биссектрисы ВЕ и АD треугольника АВС
пересекаются в точке Q.
Найдите площадь
треугольника АВС, если площадь треугольника
BQD равна 1, 2АС = 3 АВ, 3ВС = 4 АВ.
треугольника АВС, если площадь треугольника
BQD равна 1, 2АС = 3 АВ, 3ВС = 4 АВ.
Слайд 121. На продолжениях сторон АВ, ВС, АС треугольника АВС взяты соответственно
точки С1, А1, В1 так, что АВ = ВС1, ВС = СА1, СА = АВ1. Найдите отношение в котором прямая АВ1 делит сторону А1С1 треугольника А1В1С1.
2. Точки А1 и В1 делят стороны ВС и АС треугольника АВС в отношениях 2 : 1 и 1 : 2. Прямые АА1 и ВВ1 пересекаются в точке О. Площадь треугольника АВС равна 1. Найдите площадь треугольника ОВС.
Домашнее задание