- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теорема Виета
Содержание
- 1. Презентация по математике на тему Теорема Виета
- 2. По образованию был юристом, но глубокозанимался многиминауками,
- 3. 1591-ый год. Франция.
- 4. Квадратное уравнение.ax2 + bx
- 5. x2 – 15x + 14 = 0;
- 6. I способ.
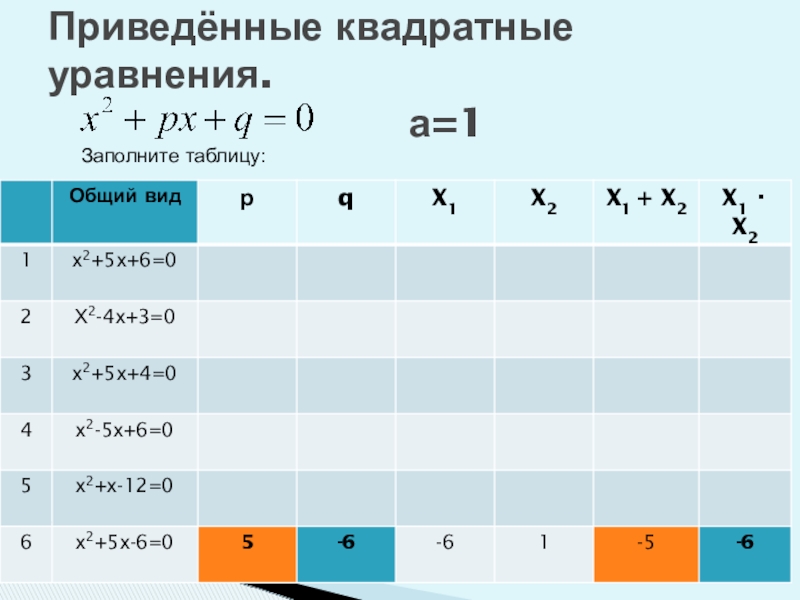
- 7. Приведённые квадратные уравнения.
- 8. Приведённые квадратные уравнения.
- 9. Приведённые квадратные уравнения.
- 10. Приведённые квадратные уравнения.
- 11. Приведённые квадратные уравнения.
- 12. Приведённые квадратные уравнения.
- 13. Приведённые квадратные уравнения.
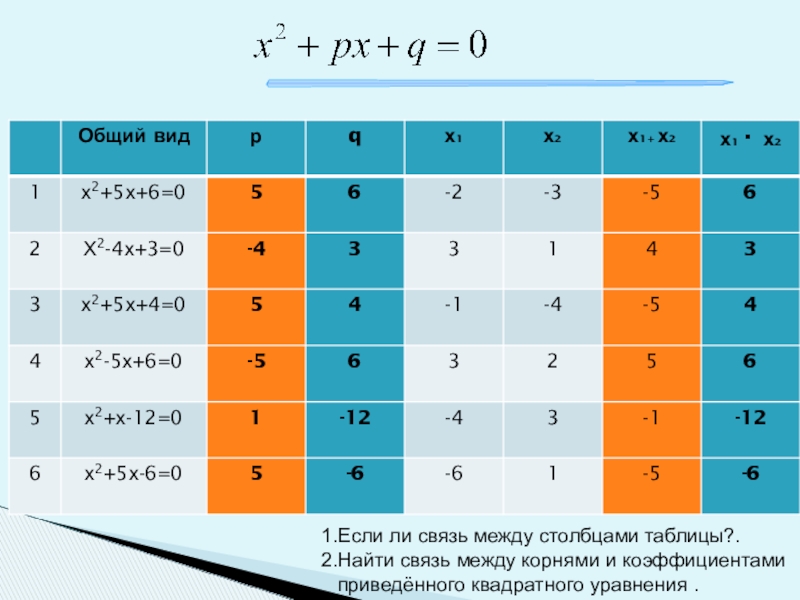
- 14. 1.Если ли связь между столбцами таблицы?.2.Найти связь между корнями и коэффициентами приведённого квадратного уравнения .
- 15. Сумма корней приведённого квадратного уравнения равна второму
- 16. Пусть х1 и х2 – корни приведённого
- 17. ax2 + bx + c =0-oбщий вид
- 18. Пусть х1 и х2 – корни квадратного
- 19. х2 +
- 20. Теорема Виета.Пустьх1 и
- 21. x2+b/ax+c/a=0По праву достойна в стихах быть
- 22. Дано:
- 23. Доказательство теоремы: Дано: аx2+bx
- 24. Образец записи1.Найти сумму и
- 25. Рефлексия.Кто же запомнил теорему Виета?Когда можно её применять?D≥0Зачем нужна?Упрощает решение квадратных уравнений
- 26. Для составления квадратного уравнения по заданным корням.ЗАДАЧА:
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. Слайд 32
- 33. Теорема Виета.Пустьх1 и
- 34. Доказательство теоремы: Дано: аx2+bx
- 35. Замечание 1. Теорема Виета справедлива и в
- 36. Приведённые квадратные уравнения.
- 37. Найдите связь между корнями и коэффициентами приведённого квадратного уравнения .Заполните таблицу:
- 38. Сумма корней приведённого квадратного уравнения равна второму
- 39. x2+b/ax+c/a=0По праву достойна в стихах быть
- 40. Доказательство теоремы: Дано: x2+bx
- 41. Дано:
- 42. Теорема Виета
- 43. Исследование – поиск путей решения проблемы.
- 44. Родился в 1540 году во Франции в
- 45. Дано:
- 46. Решить уравнение:
- 47. а) для решения уравненийПрименение теоремы Виета:
- 48. б) для решения систем уравнений:
- 49. Для составления квадратного уравнения по заданным корням.ЗАДАЧА:
- 50. стр 150 – 151. Теорема Виета для полного квадратного уравнения.Работа с учебником:
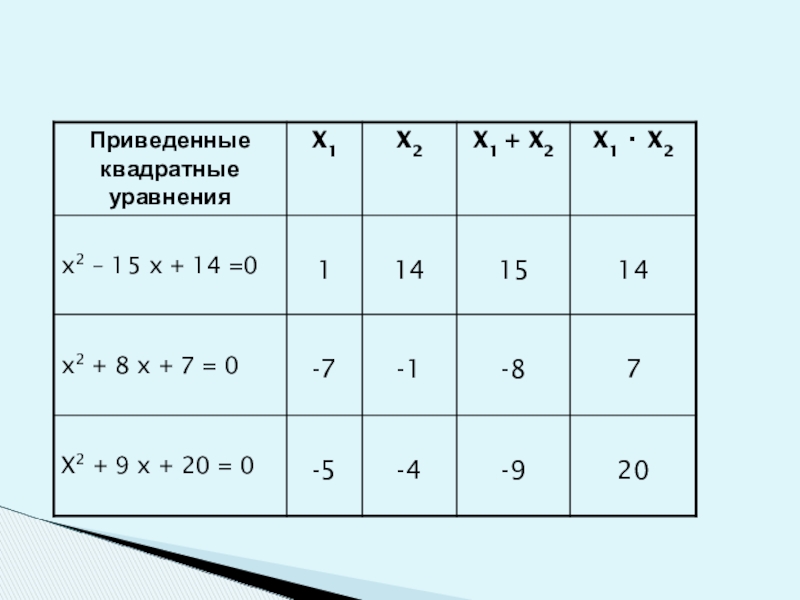
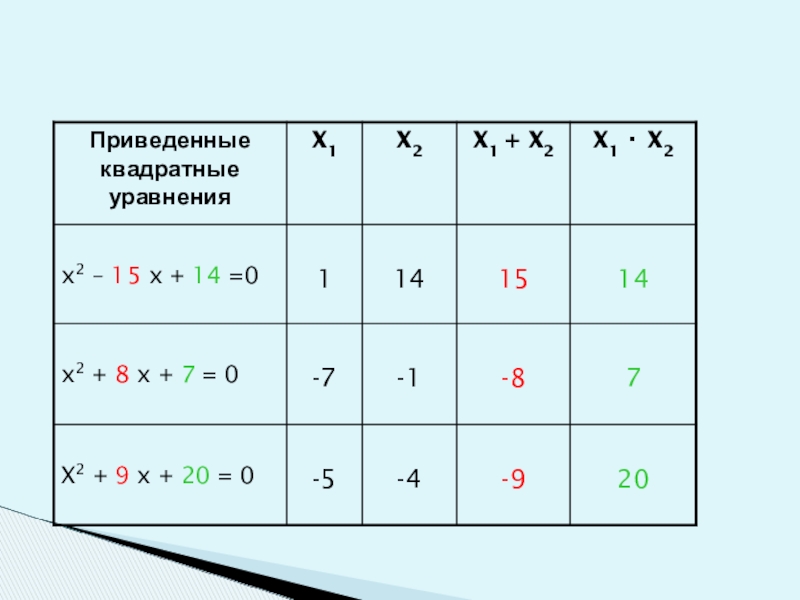
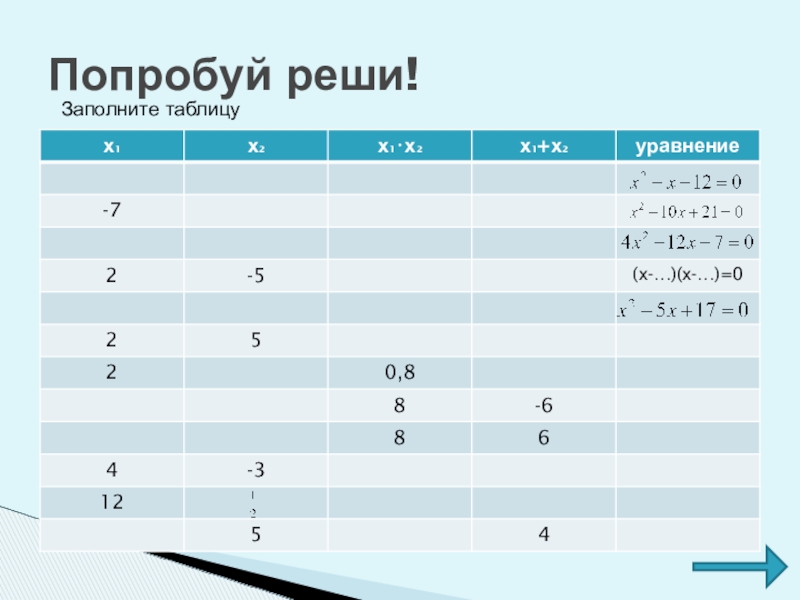
- 51. Попробуй реши!Заполните таблицу
- 52. 1 случай:2 случай:Это интересно (дополнительные сведения о нахождении корней квадратного уравнения в особых случаях):
- 53. Нахождение корней приведенного квадратного уравнения с чётным
- 54. «Пэ», со знаком взяв обратным,Мы на два
- 55. П 24 стр 150 - 151№ 961,963Написать
- 56. Ребята, вы сегодня молодцы!До новых встреч!
- 57. 1. Квадратное.2. Приведенное.3. Равносильное.4. Коэффициент.5. Корень.6. Уравнение.7.
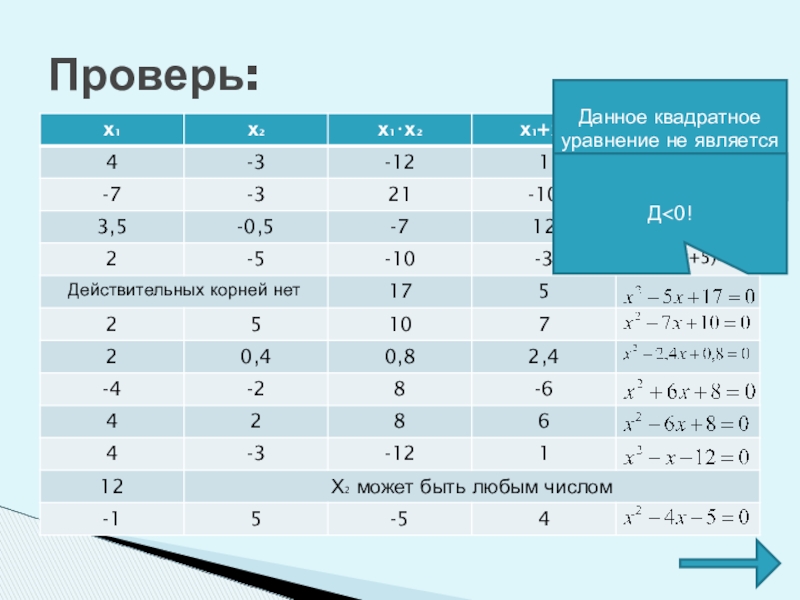
- 58. Проверь:Данное квадратное уравнение не является приведённым!Д
- 59. К середине XVI века в Европе уже
- 60. Посредством уравнений, теоремОн уйму всяких разрешал проблем:И
- 61. 1. Уравнение вида ах²+вх+с=о2.Квадратные уравнения, у которых
Слайд 2По образованию был
юристом, но глубоко
занимался многими
науками, прежде всего
астрономией, астрологией
и даже
(тайнописью). Всё это
заставило Виета обратиться
к тригонометрии и алгебре,
в которых он сделал
немало открытий.
Франсуа Виет – французский учёный (1540 – 1603)
Слайд 31591-ый год. Франция.
х2 – 15х + 14 = 0;
9 – 2х2 – 3х = 0;
х2 + 8х + 7 = 0;
3х2 – 2х = 4;
6х2 – 2 = 6х;
х2 = - 9х – 20.
Слайд 4 Квадратное уравнение.
ax2 + bx + c = 0
x2 + bx + c = 0 (а=1) - приведённое квадратное уравнение (а=1)
Слайд 5x2 – 15x + 14 = 0;
9 – 2x2 –
3) x2 + 8x + 7 = 0;
4) 3x2 – 2x = 4;
5) 6x2 – 2 = 6x;
6) x2 = - 9x – 20.
Слайд 6 I способ.
X2 – 15x + 14 = 0 9 – 2x2 – 3x = 0
X2 + 8x + 7 = 0 3x2 – 2x = 4
6x2 - 2 = 6x
x2 = - 9x – 20
II способ.
1 гр. 2 гр.
9 – 2x2 - 3x = 0 x2 – 15x + 14 = 0
3x2 – 2x = 4 x2 + 8x + 7 = 0
6x2 – 2 = 6x x2 = - 9x - 20
Слайд 141.Если ли связь между столбцами таблицы?.
2.Найти связь между корнями и коэффициентами
приведённого квадратного уравнения .
Слайд 15Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным
Слайд 16
Пусть х1 и х2 – корни приведённого квадратного уравнения x2 +
тогда х1 + х2 = - p,
x1 ∙ x2 = q.
Слайд 18Пусть х1 и х2 – корни квадратного уравнения
aх2 + bx
x1 + x2 = - b/a,
x1 ∙ x2 = c/a.
Слайд 19 х2 + px + q =
ax2 + bx + c =0-oбщий вид квадратного уравн.
x2 + b/ax + c/a = 0
x2 + px + q = 0
ax2 + bx + c = 0
Пусть х1 и х2 – корни квадратного уравнения
aх2 + bx + c = 0, тогда
x1 + x2 = - b/a,
x1 ∙ x2 = c/a.
Слайд 20 Теорема Виета.
Пустьх1 и х2 – корни квадратного
aх2 + bx + c = 0,
тогда сумма корней равна - b/a
( x1 + x2 = - b/a),
а произведение корней равно с/а
(x1 ∙ x2 = c/a).
Слайд 21 x2+b/ax+c/a=0
По праву достойна в стихах быть воспета
О свойствах корней теорема
Что лучше скажи, постоянства такого:
Умножишь ты корни и дробь уж готова?
В числителе c, в знаменателе a.
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда
В числителе b в знаменателе a.
Слайд 23Доказательство теоремы:
Дано: аx2+bx +c = 0,
Доказать: x1 + x2 = - b/а, х1 х2 = c/а.
Доказательство:
Слайд 24 Образец записи
1.Найти сумму и произведение корней квадратного уравнения
x2
х2 -4 х +3= 0;
х1 + х2 = - р=4
х1 ∙ х2 = q =-6
х1 =
х2 =
2.Сконструировать уравнение по его корням.
х1 = -2, х2 =5
х1 + х2 = -2+5= 3 = - р; р=-3
х1 ∙ х2 = -2 ∙ 5=-10=q
x2 + p x + q = 0,
х2 - 3 x -10 = 0.
3.Решить у доски три уравнения (D>0,D=0,D<0)
а) х2 + 5х – 6 = 0;
б) y2 – 10y + 25 = 0;
в) х2 + 9х + 22 = 0.
Слайд 25Рефлексия.
Кто же запомнил теорему Виета?
Когда можно её применять?
D≥0
Зачем нужна?
Упрощает решение квадратных
Слайд 26Для составления квадратного уравнения по заданным корням.
ЗАДАЧА: Составить квадратное уравнение, корнями
По формулам Виета имеем:
-р = 8 + (- 5) и q = 8 ⋅ (- 5)
р = - 3 q = - 40
Уравнение имеет вид:
Слайд 33 Теорема Виета.
Пустьх1 и х2 – корни квадратного
aх2 + bx + c = 0,
тогда сумма корней равна - b/a
( x1 + x2 = - b/a),
а произведение корней равно с/а
(x1 ∙ x2 = c/a).
Слайд 34Доказательство теоремы:
Дано: аx2+bx +c = 0,
Доказать: x1 + x2 = - b/а, х1 х2 = c/а.
Доказательство:
Слайд 35Замечание 1.
Теорема Виета справедлива и в том случае, когда квадратное
Слайд 37Найдите связь между корнями и коэффициентами приведённого квадратного уравнения .
Заполните таблицу:
Слайд 38Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным
Слайд 39 x2+b/ax+c/a=0
По праву достойна в стихах быть воспета
О свойствах корней теорема
Что лучше скажи, постоянства такого:
Умножишь ты корни и дробь уж готова?
В числителе c, в знаменателе a.
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда
В числителе b в знаменателе a.
Слайд 40Доказательство теоремы:
Дано: x2+bx +c = 0,
Доказать: x1 + x2 = - b, х1 х2 = c.
Доказательство:
Слайд 43Исследование – поиск путей решения проблемы.
Решите каждое квадратное уравнение известным вам способом.
Заполните рабочий лист.
Сравните результаты колонок №2 и №5 по каждому уравнению, найдите закономерность, сделайте вывод.
Сравните результаты колонок №3 и №6 по каждому уравнению, найдите закономерность, сделайте вывод.
Ответьте на вопрос урока.
Подготовьте отчет.
Одна из групп, составленная из более сильных учащихся, проводит исследование и на листах формата А3 выполняет дополнительное задание, связанное с нахождением суммы и произведения корней приведенного квадратного уравнения в общем виде.
Слайд 44
Родился в 1540 году во Франции в Фонтене-ле-Конт. По профессии адвокат.
Виет, не прекращая адвокатской деятельности, много лет был советником короля Георга III и Георга IV, постоянно был занят государственной службой. Несмотря, на это, всю жизнь занимался математикой, занимался настойчиво, упорно, сумел добиться выдающихся результатов. Основные свои идеи изложил в труде “Введение в аналитическое искусство”.
. И другие достижения Франсуа Виета.
Слайд 49Для составления квадратного уравнения по заданным корням.
ЗАДАЧА: Составить квадратное уравнение, корнями
По формулам Виета имеем:
-р = 8 + (- 5) и q = 8 ⋅ (- 5)
р = - 3 q = - 40
Уравнение имеет вид:
Слайд 521 случай:
2 случай:
Это интересно (дополнительные сведения о нахождении корней квадратного уравнения
Слайд 53Нахождение корней приведенного квадратного уравнения с чётным коэффициентом q: х²+px+q=0. Здесь
Формула запоминается надолго, если выучить ее в стихотворной форме:
Слайд 54«Пэ», со знаком взяв обратным,
Мы на два его разделим.
Корень от него
Мы аккуратненько отделим.
А под корнем, очень кстати,
Половина «пэ» в квадрате,
Минус «ку». И вот решенье
Небольшого уравненья.
Стихотворение для запоминания формулы
Слайд 55П 24 стр 150 - 151
№ 961,
963
Написать реферат на одну из
«Применение теоремы Виета»
«Утверждения, следующие из теоремы Виета»
«Корни квадратного уравнения и теорема Виета»
«Что нового я узнал, благодаря теореме Виета»
«Вокруг теоремы Виета»
Домашнее задание:
Слайд 571. Квадратное.
2. Приведенное.
3. Равносильное.
4. Коэффициент.
5. Корень.
6. Уравнение.
7. Арифметический.
8. Диофант.
9. Неполное.
10. Различитель.
11.
12. Виет.
В выделенном столбце : ДИСКРИМИНАНТ
Ответы к кроссворду:
Слайд 59К середине XVI века в Европе уже успешно применяли буквы для
Впервые это сделал знаменитый французский учёный Франсуа Виет (1540 – 1603), которого именно за это новшество называют «отцом алгебры».
Сам «отец алгебры» не признавал слово «алгебра», считал его языческим, варварским. То, чем он занимался, Франсуа Виет называл «аналитическим искусством»
Историческая справка:
Слайд 60Посредством уравнений, теорем
Он уйму всяких разрешал проблем:
И засуху предсказывал и ливни.
Поистине
Д. Чосер
(Джефри Чосер (1340 – 1400) – английский поэт)
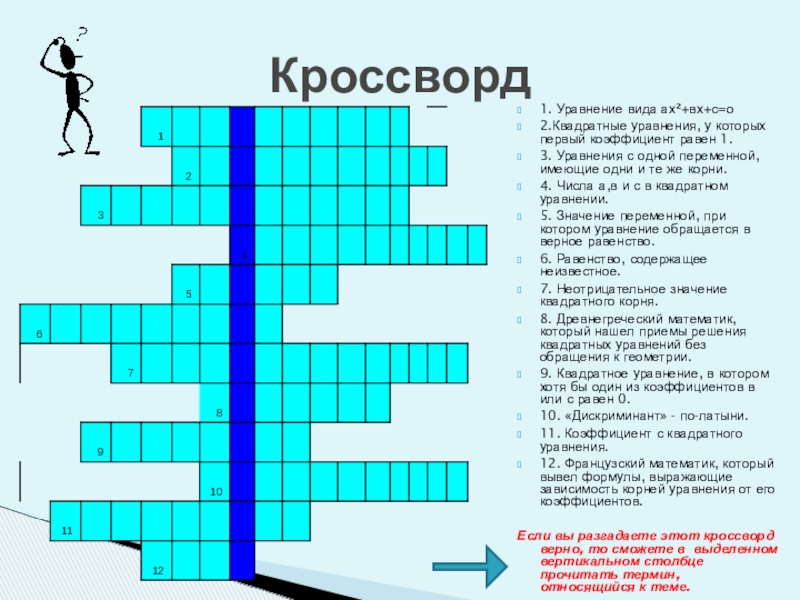
Слайд 611. Уравнение вида ах²+вх+с=о
2.Квадратные уравнения, у которых первый коэффициент равен 1.
3.
4. Числа а,в и с в квадратном уравнении.
5. Значение переменной, при котором уравнение обращается в верное равенство.
6. Равенство, содержащее неизвестное.
7. Неотрицательное значение квадратного корня.
8. Древнегреческий математик, который нашел приемы решения квадратных уравнений без обращения к геометрии.
9. Квадратное уравнение, в котором хотя бы один из коэффициентов в или с равен 0.
10. «Дискриминант» - по-латыни.
11. Коэффициент с квадратного уравнения.
12. Французский математик, который вывел формулы, выражающие зависимость корней уравнения от его коэффициентов.
Если вы разгадаете этот кроссворд верно, то сможете в выделенном вертикальном столбце прочитать термин, относящийся к теме.
Кроссворд