- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теорема Виета (8 класс)
Содержание
- 1. Презентация по математике на тему Теорема Виета (8 класс)
- 2. Цель урока:узнать, в чем
- 3. «Уравнения для меня важнее, потому что политика
- 4. Проверка Д/З:№563аba + b = 23 b
- 5. №541д) корней нете) -11 и 2№546Критерий оценки:
- 6. Устно: найдите приведённые квадратные уравнения:х2 + 3х
- 7. Заполните таблицу: 3-12-3-61-5-6-341-12-3-4-712 35815Какая закономерность между корнями
- 8. В 1591 г. Ф. Виет – знаменитый
- 9. Теорема Виета: Сумма корней приведённого квадратного уравнения
- 10. aх2 + bх + c = 0
- 11. Самостоятельная работа18 и -19 и 2-9 и 2-6 и -39 и 4
- 12. Д/З: п.24, №580(д - з), 583
- 13. Флажок красного цвета: «Я удовлетворен уроком, урок
- 14. Литература:1) Алгебра: учебник для
Цель урока:узнать, в чем заключается теорема Виета;- доказать теорему Виета;- познакомиться с ее применением при решении квадратных уравнений.
Слайд 2
Цель урока:
узнать, в чем заключается теорема Виета;
- доказать
теорему Виета;
- познакомиться с ее применением при решении квадратных уравнений.
Слайд 3«Уравнения для меня важнее, потому что политика – для настоящего, а
уравнения – для вечности»
Альберт Эйнштейн
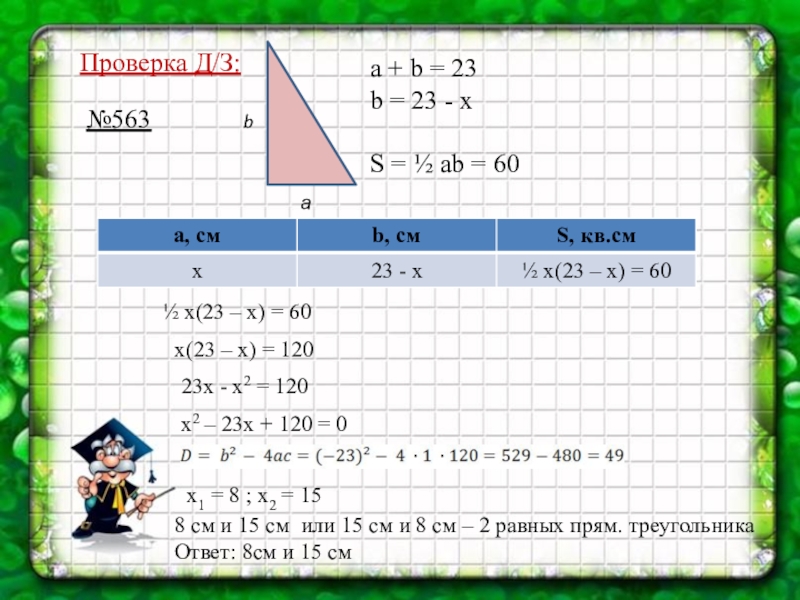
Слайд 4Проверка Д/З:
№563
а
b
a + b = 23
b = 23 - x
S = ½ ab = 60
½ x(23 – x) = 60
x(23 – x) = 120
23х - х2 = 120
х2 – 23х + 120 = 0
x1 = 8 ; х2 = 15
8 см и 15 см или 15 см и 8 см – 2 равных прям. треугольника
Ответ: 8см и 15 см
Слайд 6Устно:
найдите приведённые квадратные уравнения:
х2 + 3х + 2 = 0
-2х2
+ 3х - 6 = 0
х2 - 5х + 56 = 0
х2 - 7х + 16 = 0
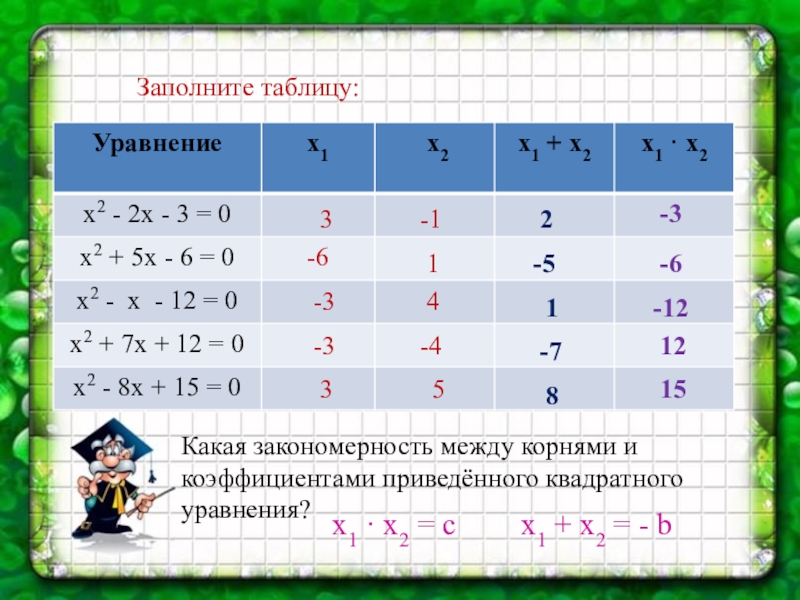
Слайд 7Заполните таблицу:
3
-1
2
-3
-6
1
-5
-6
-3
4
1
-12
-3
-4
-7
12
3
5
8
15
Какая закономерность между корнями и коэффициентами приведённого квадратного
уравнения?
x1 · х2 = с
x1 + х2 = - b
Слайд 8В 1591 г. Ф. Виет – знаменитый французский математик - вывел
формулы, выражающие зависимость корней квадратного уравнения
от его коэффициентов и сформулировал свою знаменитую теорему.
Именно с 1591 г. мы пользуемся формулами при решении квадратных уравнений.
1540-1603
Его называют «отцом алгебры».
Слайд 9Теорема Виета: Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому
с противоположным знаком, а произведение корней равно свободному члену.
Дано:
х2 + pх + q = 0
Доказать:
x1 + х2 = -p
x1 · х2 = q
Доказательство:
Слайд 13Флажок красного цвета: «Я удовлетворен уроком, урок был полезен для меня,
я много, с пользой и хорошо работал на уроке, я получил заслуженную оценку, я понимал все, о чем говорилось и что делалось на уроке»
Флажок синего цвета: «Урок был интересен и я принимал в нем активное участие, урок был в определенной степени полезен для меня, я отвечал с места, я сумел выполнить ряд заданий, мне было на уроке достаточно комфортно»
Флажок желтого цвета: «Пользы от урока я получил мало, я не очень понимал, о чем идет речь, мне это не очень нужно, домашнее задание я не понял, к ответу на уроке я не был готов»
Флажок синего цвета: «Урок был интересен и я принимал в нем активное участие, урок был в определенной степени полезен для меня, я отвечал с места, я сумел выполнить ряд заданий, мне было на уроке достаточно комфортно»
Флажок желтого цвета: «Пользы от урока я получил мало, я не очень понимал, о чем идет речь, мне это не очень нужно, домашнее задание я не понял, к ответу на уроке я не был готов»
Рефлексия
Слайд 14
Литература:
1) Алгебра: учебник для 8 кл. общеобразовательных учреждений.
Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.В. Суворов.; под редакцией С.А. Теляковского. Просвещение, 2014
2) Ковалёва Г.И. Уроки математики в 8-м классе. Поурочные планы. Часть II. – Волгоград, издательство «Братья Гринины», 2002
3) шаблон.45gif
4) http://fb.ru/article/214119/otets-algebryi-matematik-fransua-viet
2) Ковалёва Г.И. Уроки математики в 8-м классе. Поурочные планы. Часть II. – Волгоград, издательство «Братья Гринины», 2002
3) шаблон.45gif
4) http://fb.ru/article/214119/otets-algebryi-matematik-fransua-viet
