- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Степенные функции
Содержание
- 1. Презентация по математике на тему Степенные функции
- 2. Степенными функциями называются функции вида у = хr, где r – заданное рациональное число
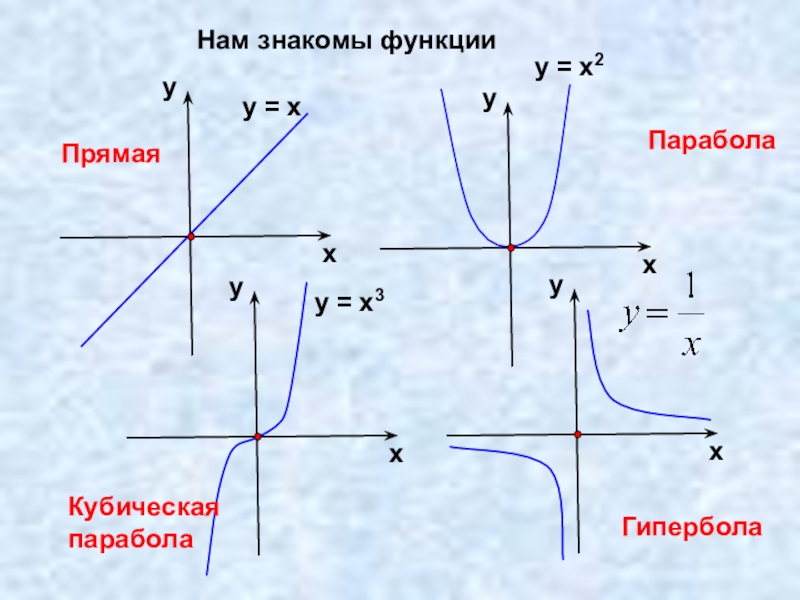
- 3. Нам знакомы функцииПрямаяПараболаКубическая параболаГипербола
- 4. yx -1 0 1 2у
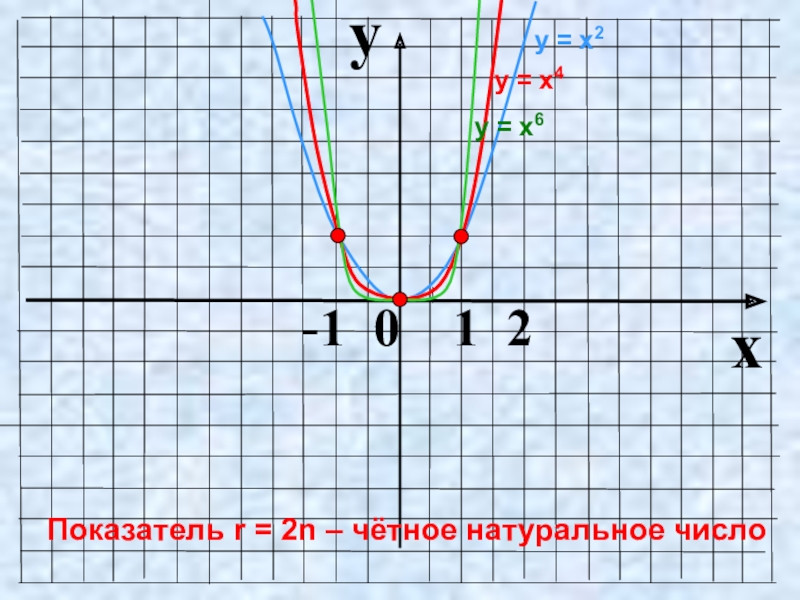
- 5. Показатель r = 2n – чётное натуральное
- 6. yx -1 0 1 2у
- 7. Показатель r = 2n-1 – нечётное
- 8. yx -1 0 1 2у
- 9. Показатель r = – (2n-1), где n
- 10. yx -1 0 1 2у
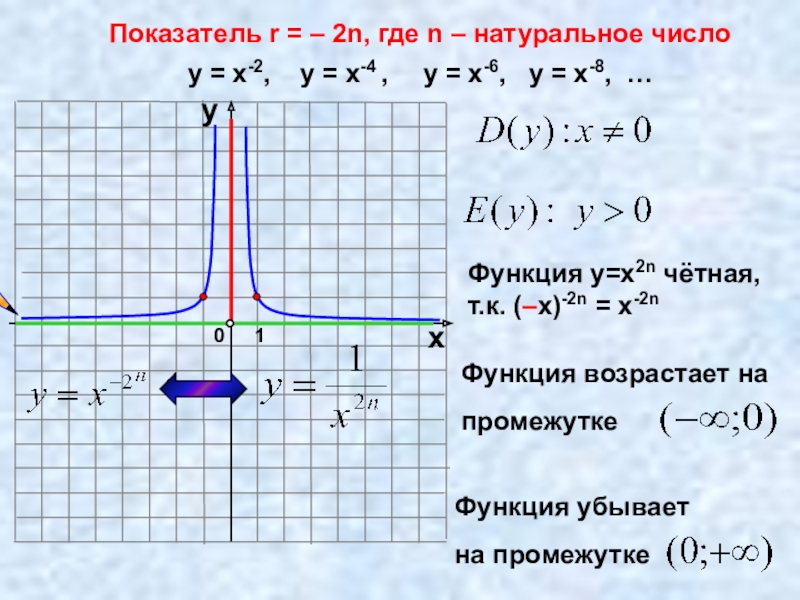
- 11. Показатель r = – 2n, где n
- 12. yx -1 0 1 2у
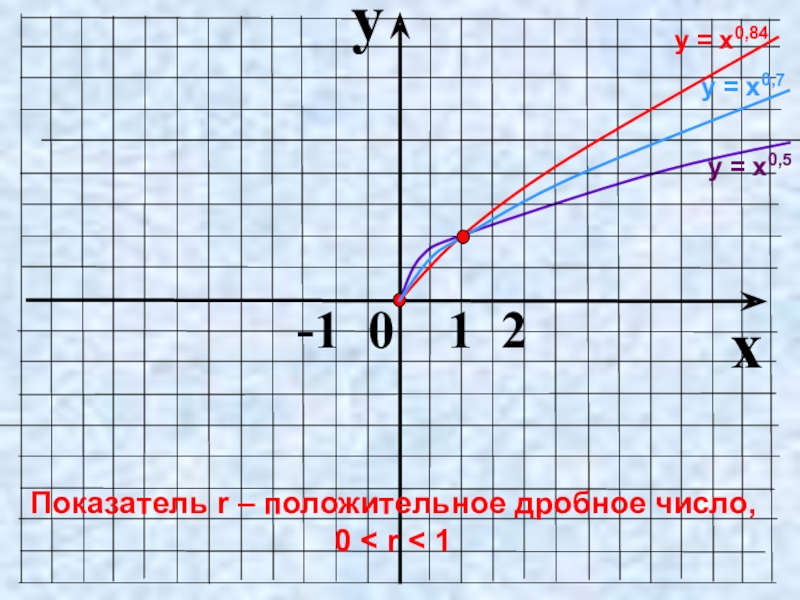
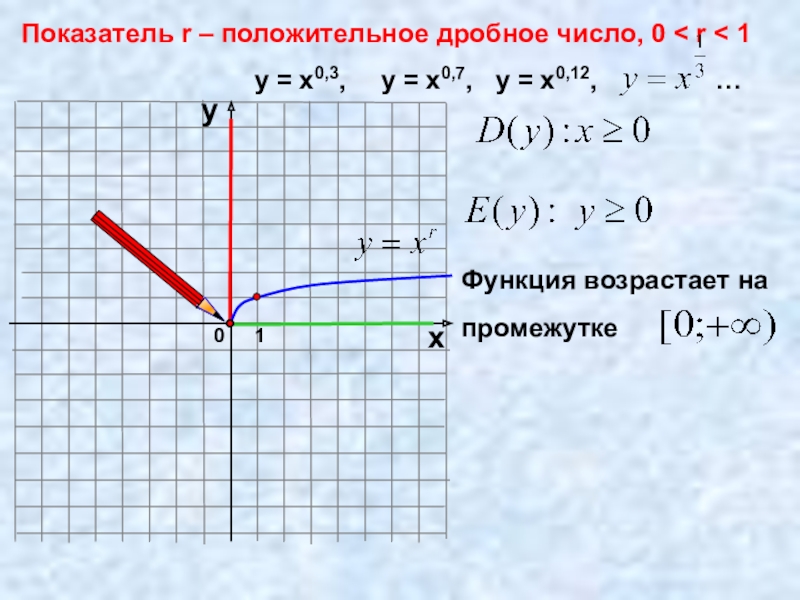
- 13. 0Показатель r – положительное дробное число, 0
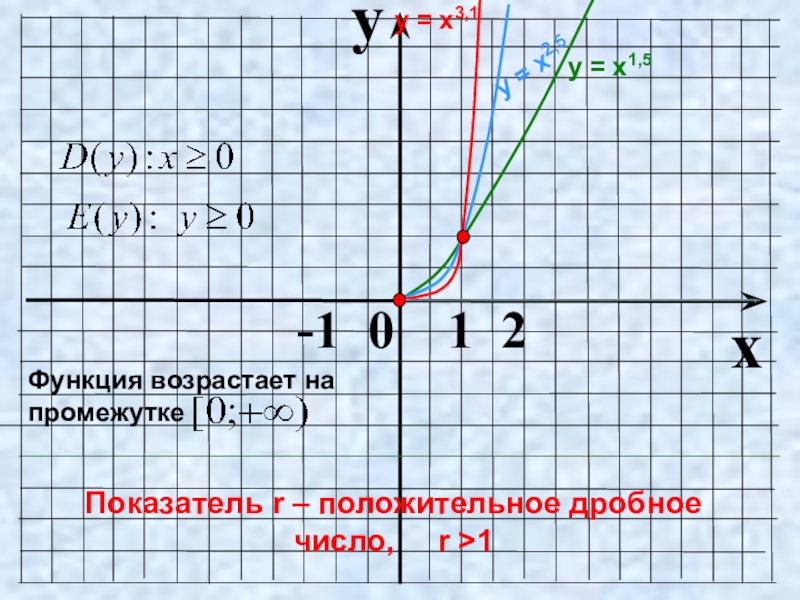
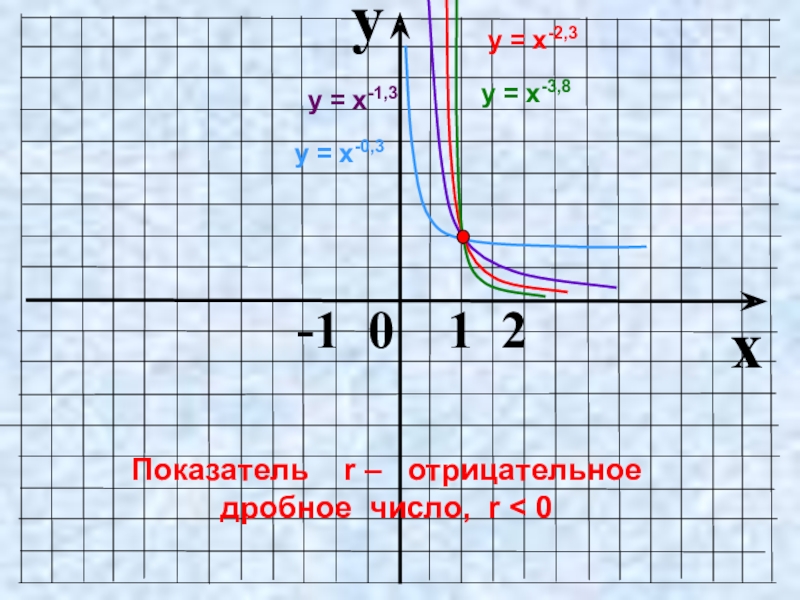
- 14. yx -1 0 1 2Показатель
- 15. yx -1 0 1 2Показатель
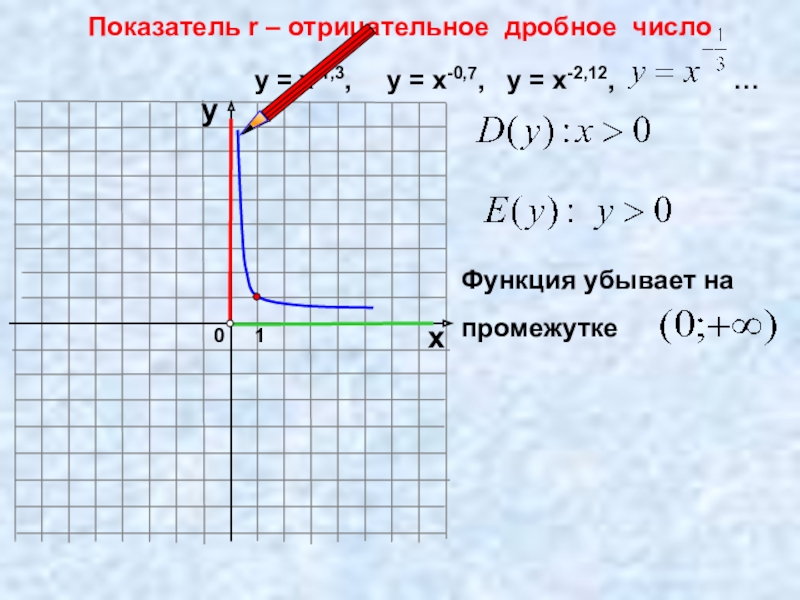
- 16. 0Показатель r – отрицательное дробное число1хуу =
- 17. Слайд 17
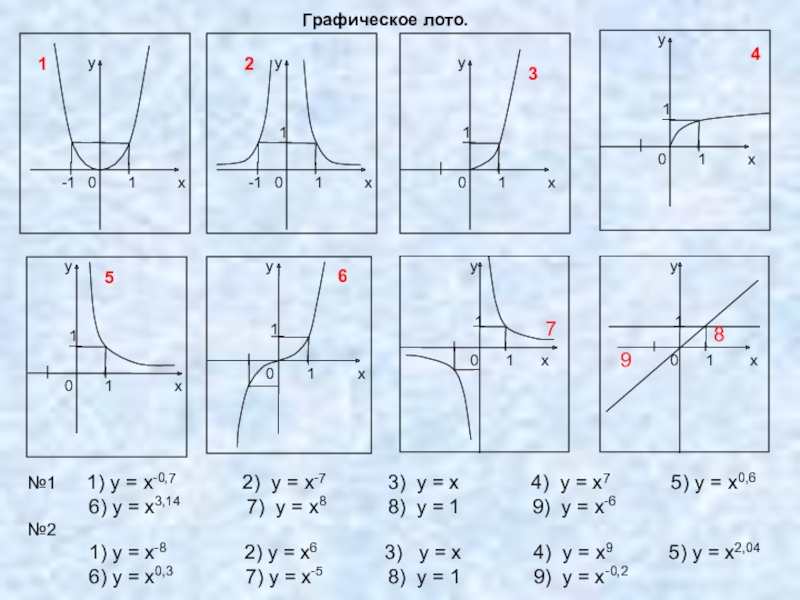
- 18. ПРАВИЛЬНЫЙ ОТВЕТ: №1 796 514 238 №2 215 694 738
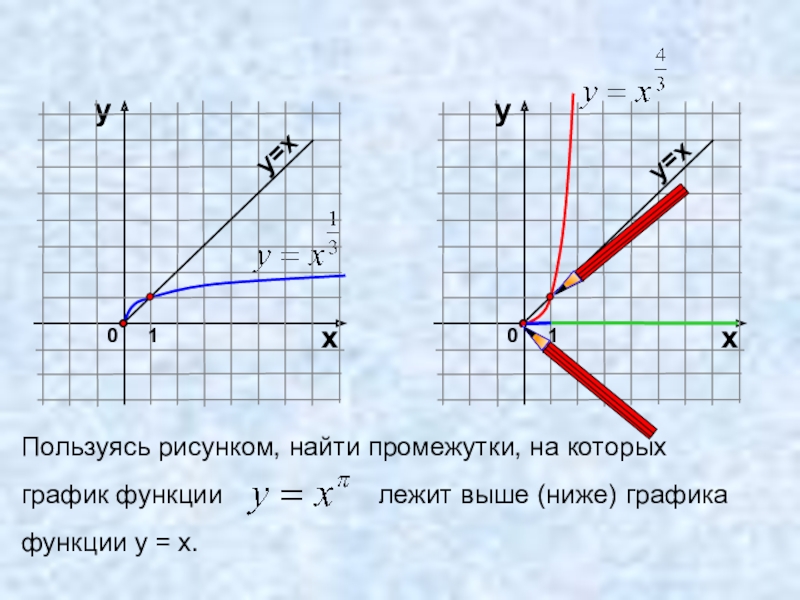
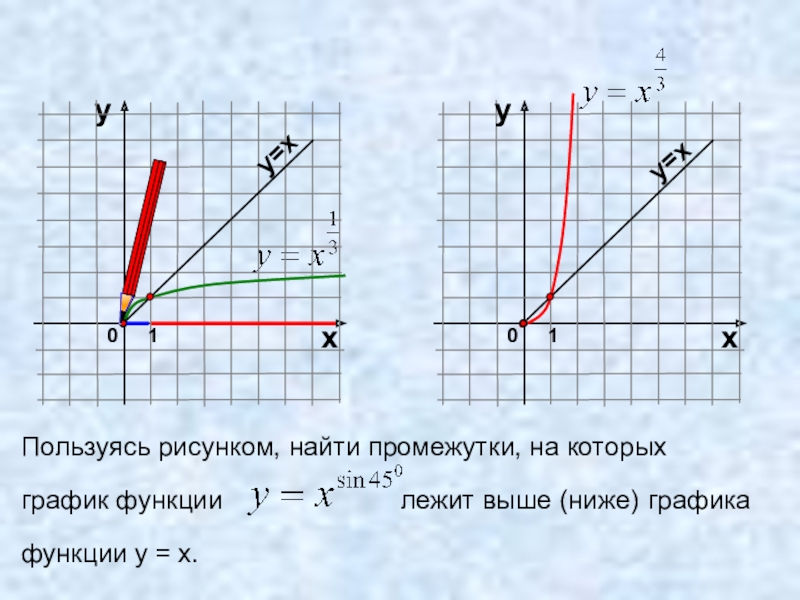
- 19. Пользуясь рисунком, найти промежутки, на которых график
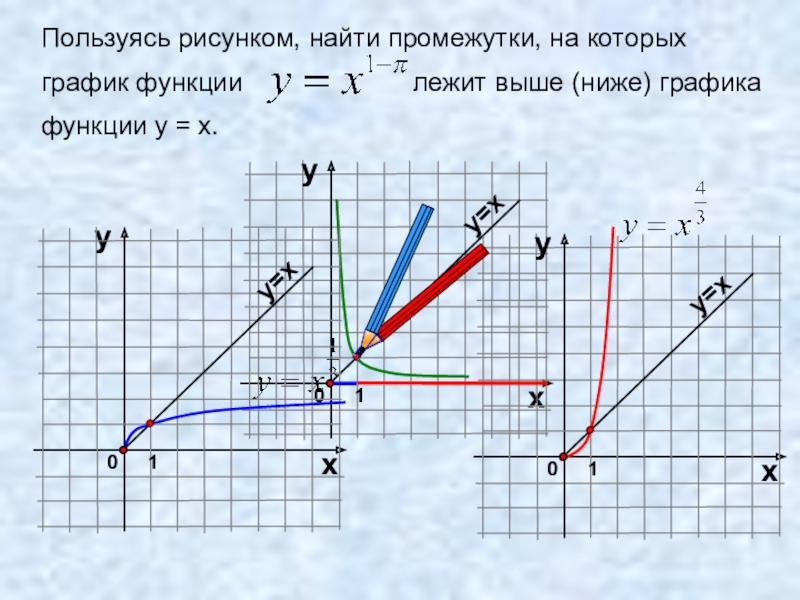
- 20. Пользуясь рисунком, найти промежутки, на которых график
- 21. Пользуясь рисунком, найти промежутки, на которых график
- 22. Преобразования графиков степенных функций
- 23. yx -1 0 1 2у = х-4у = (х – 2)-4
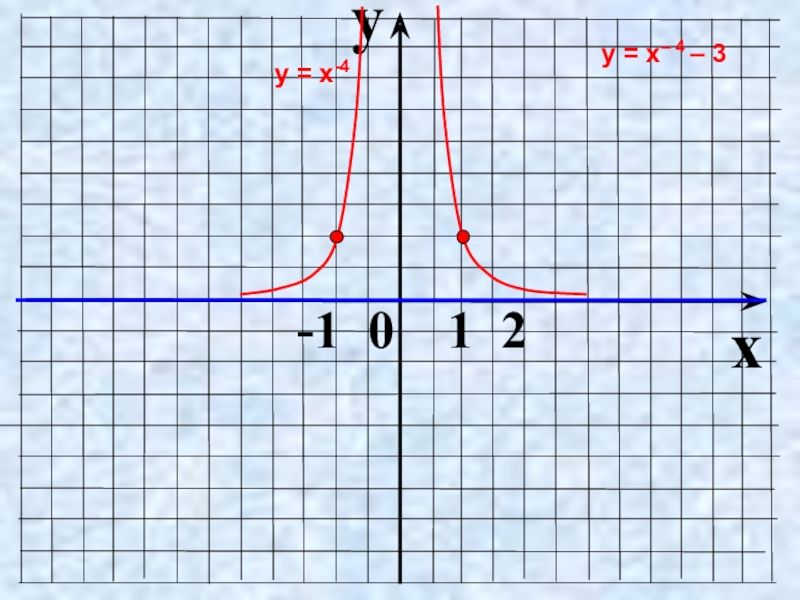
- 24. yx -1 0 1 2у = х-4у = х– 4 – 3
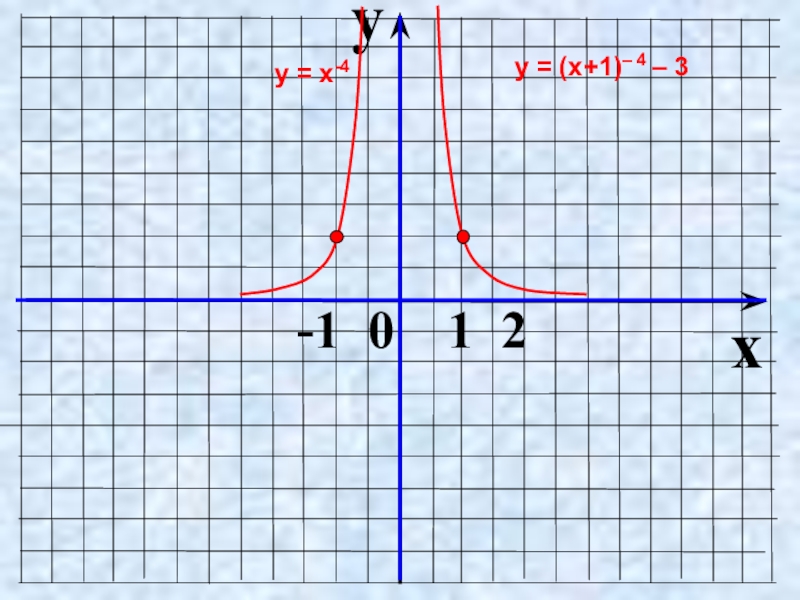
- 25. yx -1 0 1 2у = х-4у = (х+1)– 4 – 3
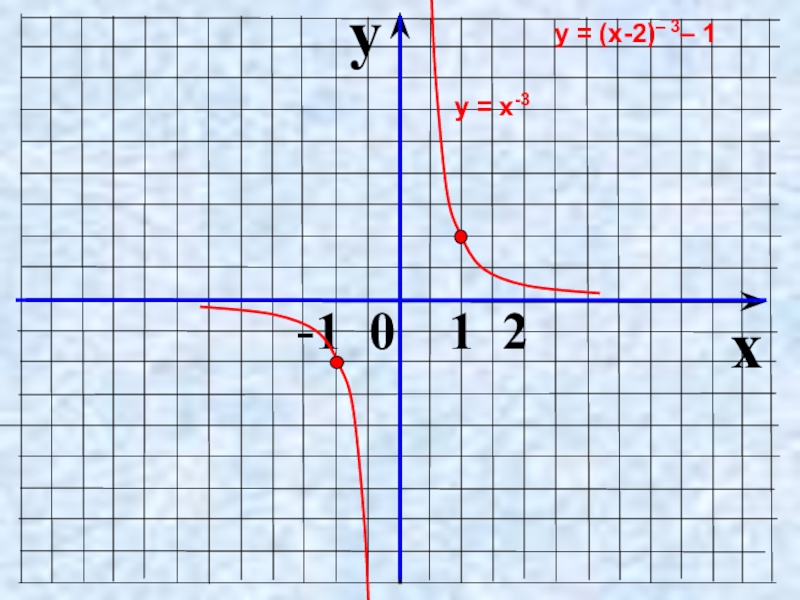
- 26. yx -1 0 1 2у = х-3у = (х-2)– 3– 1
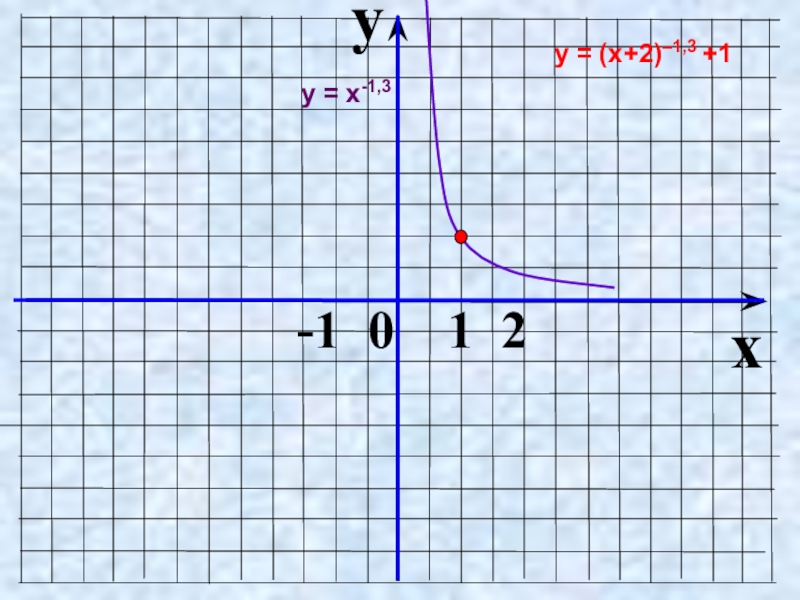
- 27. yx -1 0 1 2у = (х+2)–1,3 +1у = х-1,3
- 28. Сегодня на урокемы расширили знания о степенных функциях, их свойствах и графиках
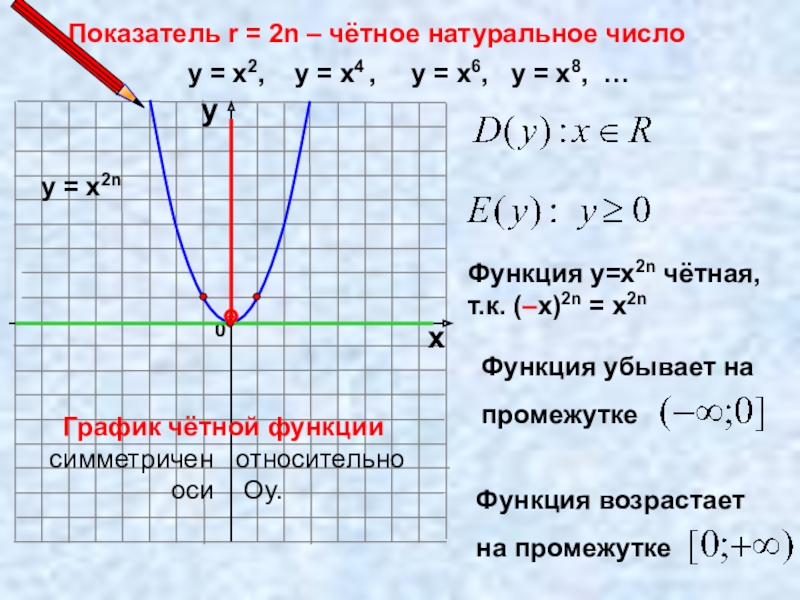
Слайд 5Показатель r = 2n – чётное натуральное число
0
х
у
у = х2,
у = х2n
Функция у=х2n чётная,
т.к. (–х)2n = х2n
График чётной функции
симметричен относительно
оси Оу.
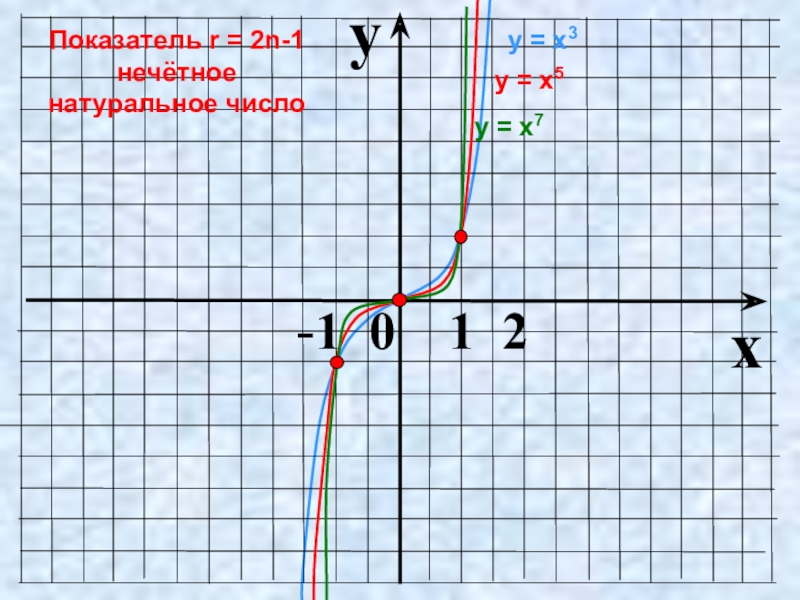
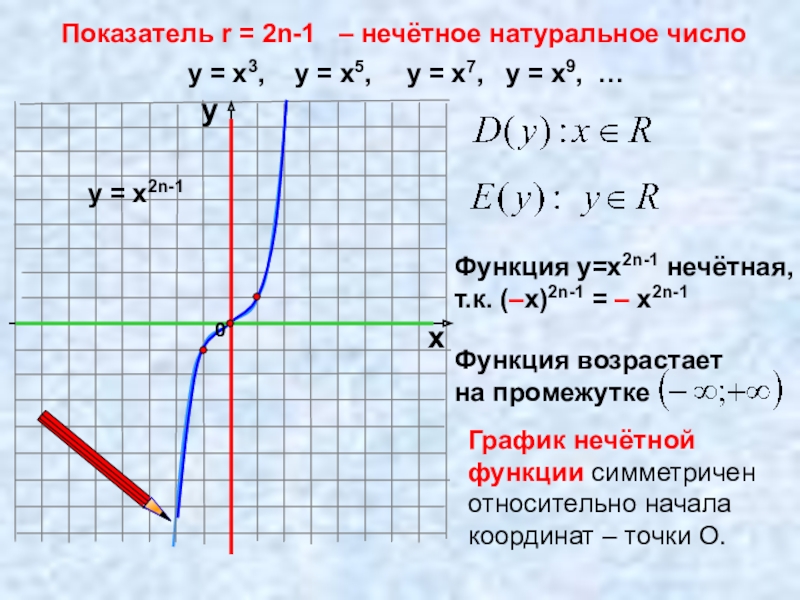
Слайд 7Показатель r = 2n-1 – нечётное натуральное число
х
у
у = х3,
у = х2n-1
Функция у=х2n-1 нечётная,
т.к. (–х)2n-1 = – х2n-1
0
График нечётной функции симметричен относительно начала координат – точки О.
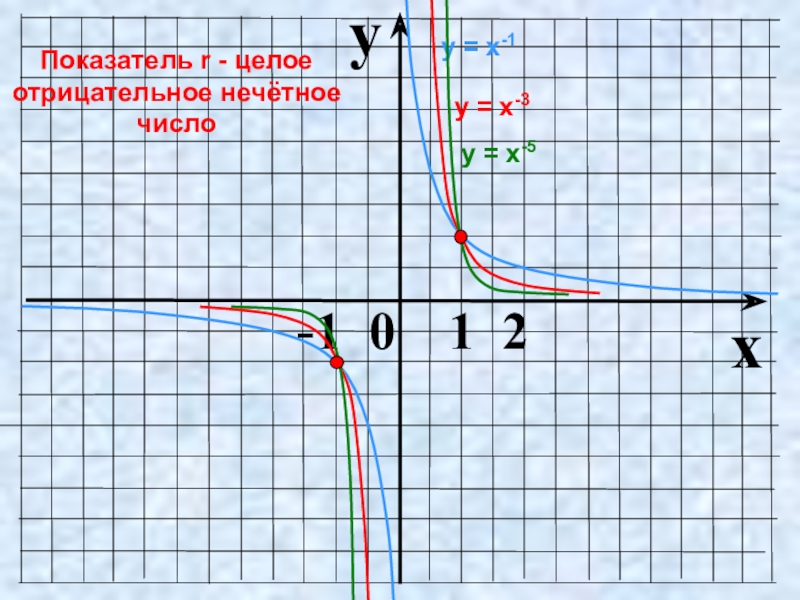
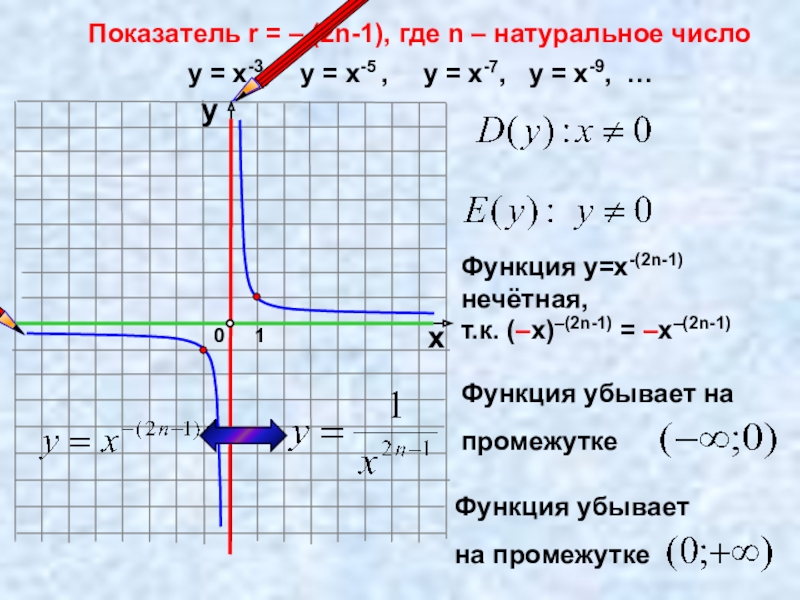
Слайд 9Показатель r = – (2n-1), где n – натуральное число
1
0
х
у
у =
Функция у=х-(2n-1) нечётная,
т.к. (–х)–(2n-1) = –х–(2n-1)
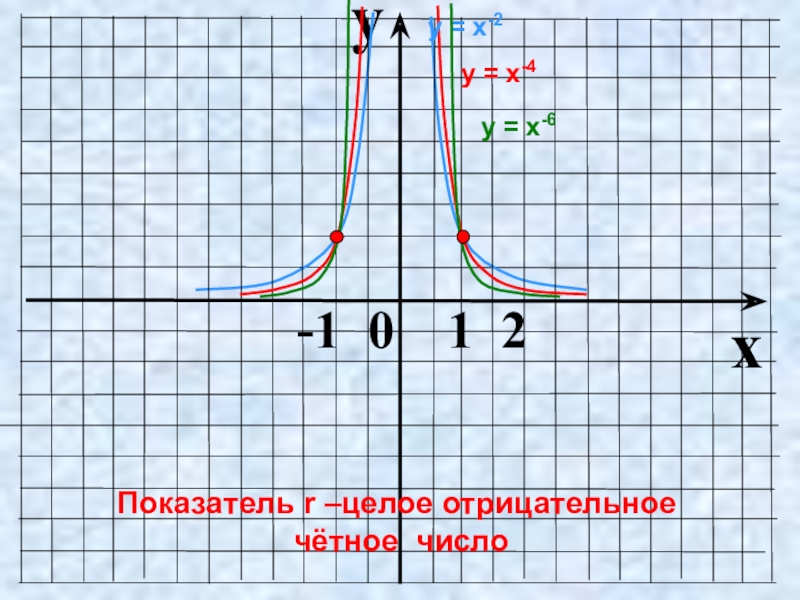
Слайд 11Показатель r = – 2n, где n – натуральное число
1
0
х
у
у =
Функция у=х2n чётная,
т.к. (–х)-2n = х-2n
Слайд 17
8
7
9
№1 1) у = х-0,7 2) у = х-7 3) у = х 4) у = х7 5) у = х0,6
6) у = х3,14 7) у = х8 8) у = 1 9) у = х-6
№2
1) у = х-8 2) у = х6 3) у = х 4) у = х9 5) у = х2,04
6) у = х0,3 7) у = х-5 8) у = 1 9) у = х-0,2
Слайд 19Пользуясь рисунком, найти промежутки, на которых
график функции
функции у = х.
0
1
х
у
у=х
Слайд 20Пользуясь рисунком, найти промежутки, на которых
график функции
функции у = х.
у
0
1
х
у=х
Слайд 21Пользуясь рисунком, найти промежутки, на которых
график функции
функции у = х.