- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Решение задач с помощью систем уравнений 9 класс.
Содержание
- 1. Презентация по математике на тему Решение задач с помощью систем уравнений 9 класс.
- 2. Тема урока: Решение задач с помощью систем
- 3. Цели и задачи урока:Систематизировать и повторить знания
- 4. Актуализация опорных знаний. Два уравнения с двумя
- 5. В классе 25 учащихся. При посадке деревьев
- 6. х- девочек, у – мальчиков;
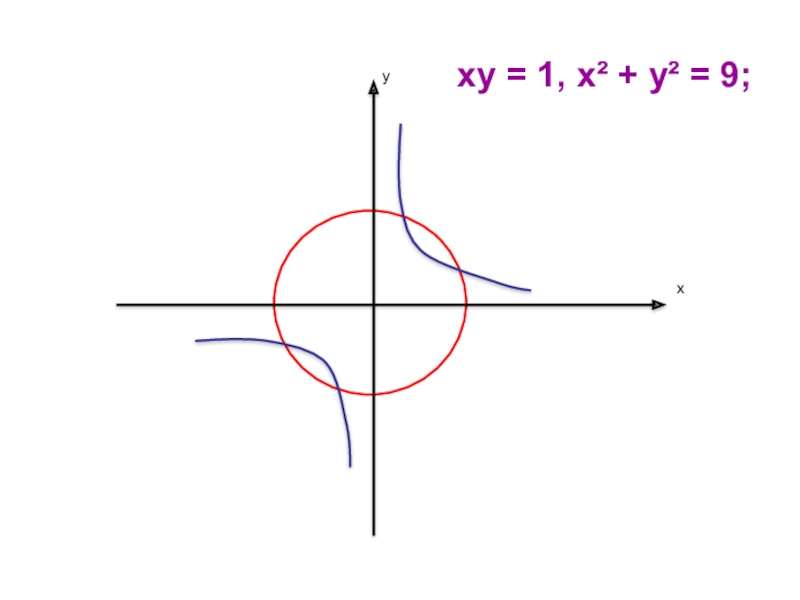
- 7. Применяя графические представления, выясните сколько решений имеет система уравнений:ху = 1, х² + у² = 9.
- 8. yx
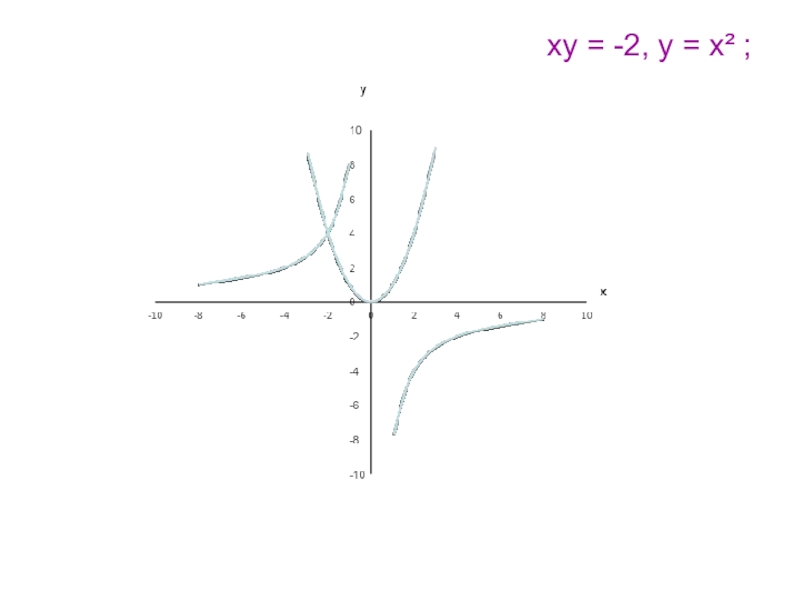
- 9. Применяя графические представления, выясните сколько решений имеет система уравнений:ху = -2, у =х²
- 10. ху = -2, у = х² ;
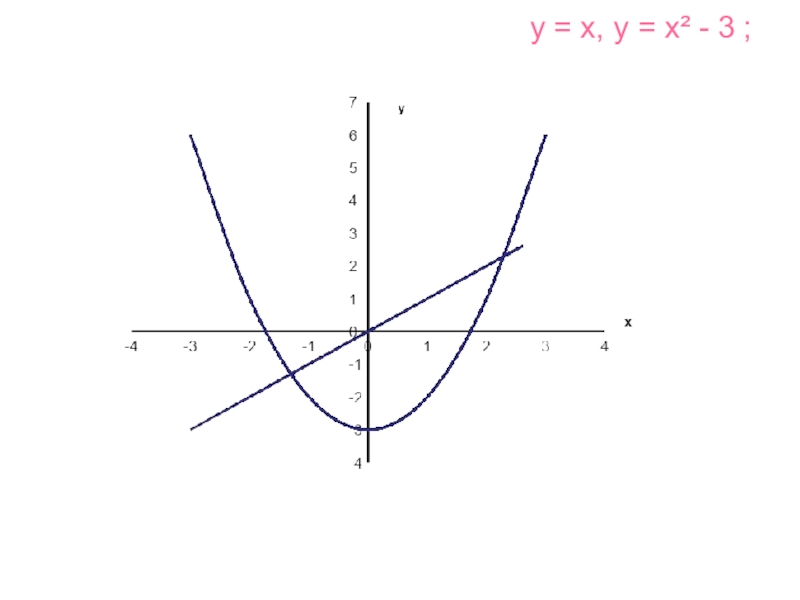
- 11. Применяя графические представления, выясните сколько решений имеет система уравнений:у = х, у = х² - 3.
- 12. у = х, у = х² - 3 ;
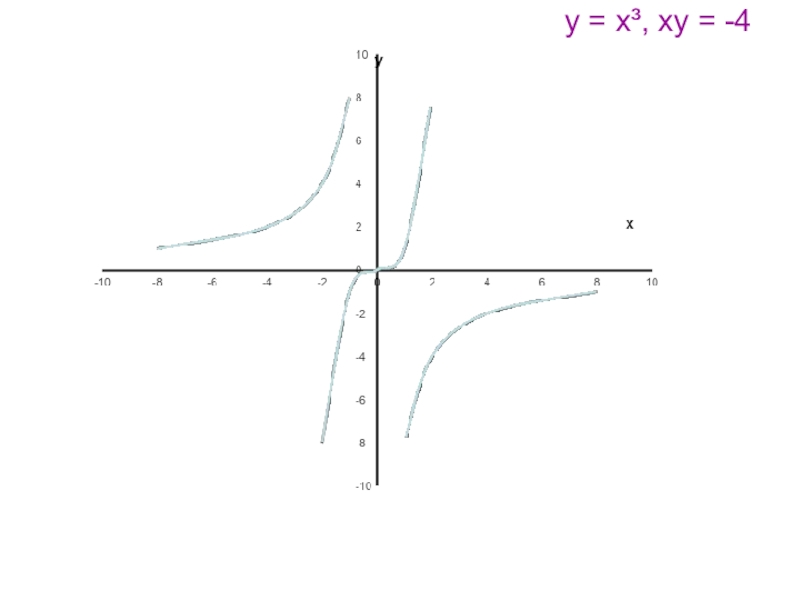
- 13. Применяя графические представления, выясните сколько решений имеет система уравнений:у = х³, ху = - 4.
- 14. у = х³, ху = -4
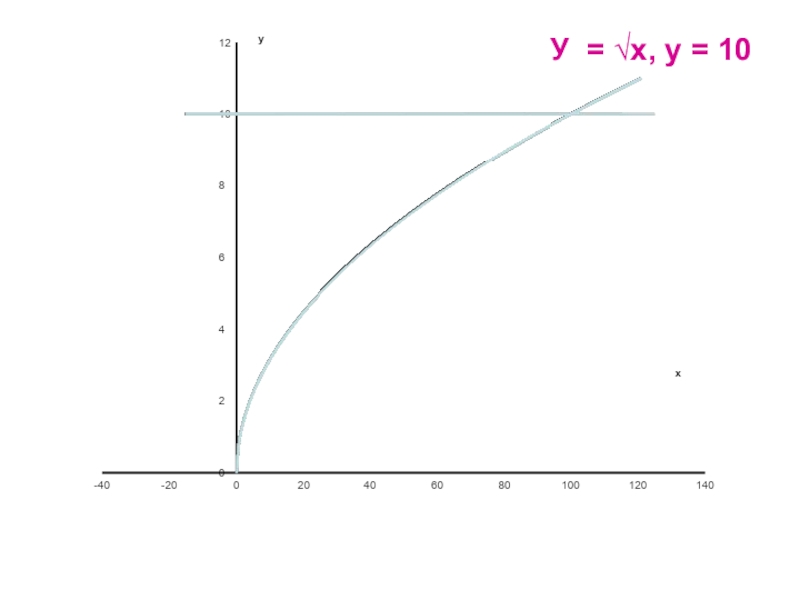
- 15. Применяя графические представления, выясните сколько решений имеет система уравнений:У = √х, у = 10.
- 16. У = √х, у = 10
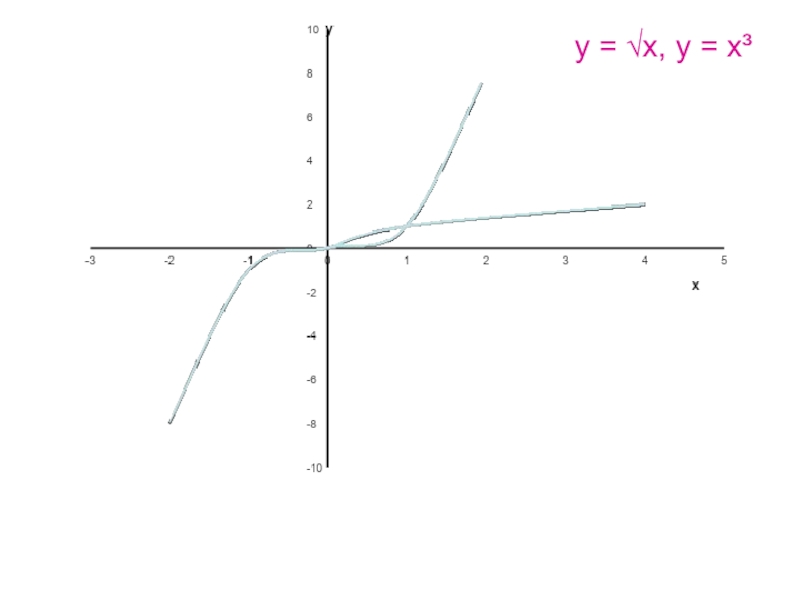
- 17. Применяя графические представления, выясните сколько решений имеет система уравнений:У = х³, у = √х.
- 18. у = √х, у = х³
- 19. Применяя графические представления, выясните сколько решений имеет
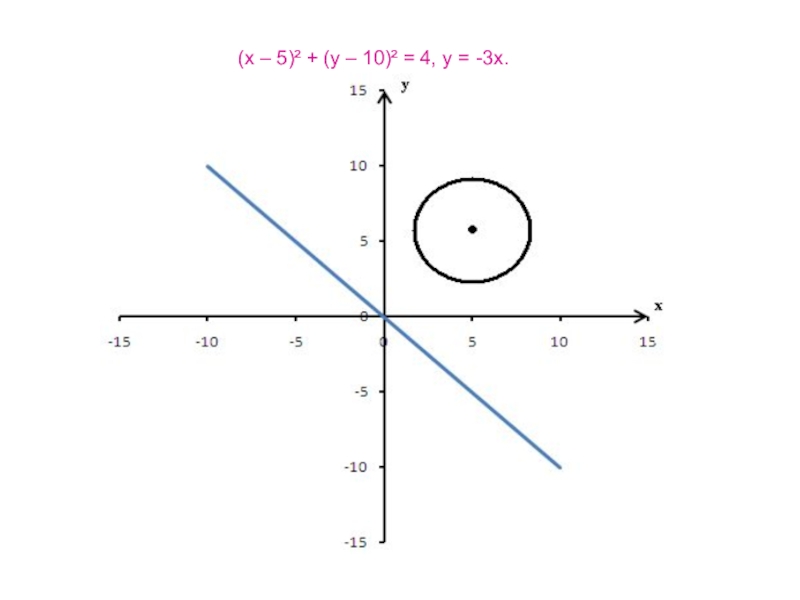
- 20. (х – 5)² + (у – 10)² = 4, у = -3х.
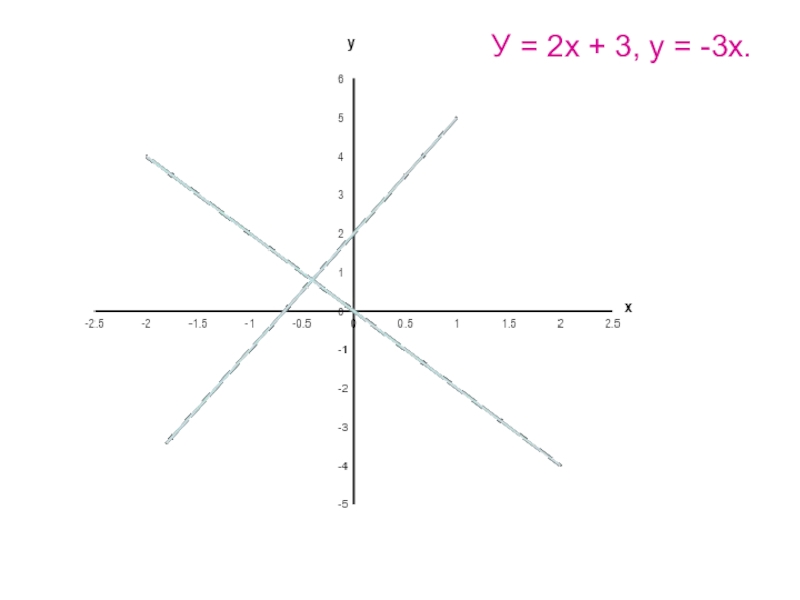
- 21. Применяя графические представления, выясните сколько решений имеет система уравнений:У = 2х +3, у = - 2х
- 22. У = 2х + 3, у = -3х.
- 23. Биллион – миллиард.Близнецы – два простых числа
- 24. Гипотенуза прямоугольного треугольника равна 20 сантиметрам. Найдите
- 25. Прямоугольный треугольник.Гипотенуза – 20 см.Катеты: х, у;Один
- 26. Пятый член арифметической прогрессии равен 8,4, а
- 27. Проверь себя!Арифметическая прогрессия: пятнадцатый член = 20,4.Геометрическая
- 28. Решите системы уравнений из сборника заданий для
- 29. Спасибо за урок!
Слайд 1МОУ «Наваринская ООШ им. Прокопьева С.Н.»
Урок математики в 9 классе по
«Решение задач с помощью систем уравнений»
Разработала:
учитель математики
А.С. Шаянова
2018 г.
Слайд 2Тема урока: Решение задач с помощью систем уравнений.
2016 г - ФГБОУ
Слайд 3Цели и задачи урока:
Систематизировать и повторить знания по алгебре и геометрии,
Развивать навыки решения задач с помощью систем уравнений и учиться применять интегрированные знания для решения текстовых задач.
Прививать интерес к математике.
Создать условия, способствующие социальной адаптации учащихся: самостоятельности, коллективизма, взаимопомощи.
Слайд 4Актуализация опорных знаний.
Два уравнения с двумя переменными, объединённые фигурными скобками
Решением системы уравнений с двумя переменными называется ……….
Решить систему уравнений – значит ……
Способы решения систем уравнений: ………
Уравнение окружности, центр которой находится в начале координат имеет вид: ……..
2
Графиком функции у = ах является ……….
Линейная функция имеет вид: ……………
Графиком линейной функции является ………..
Площадь прямоугольника вычисляется по формуле: ……
Теорема Пифагора (формулировку и формулу) ………..
Квадратичная функция имеет вид: …….
к
Графиком функции у = ------ является: ……………
Х
Прямая пропорциональность имеет вид: …………..
Периметр прямоугольника вычисляется по формуле: …
Площадь квадрата вычисляется по формуле: ……….
Слайд 5
В классе 25 учащихся. При посадке деревьев в школьном саду каждая
На дворе 20 кроликов и кур, у которых 52 ноги. Сколько кур и кроликов в отдельности?
В мастерской «Автосервис» отремонтировали 22 легковых и грузовых автомобиля. Среди них легковых на 8 меньше, чем грузовых. Сколько автомобилей каждого вида отремонтировали в мастерской?
В фермерском хозяйстве под гречиху и просо отведено 19 га, причём гречиха занимает на 5 га больше, чем просо. Сколько гектаров отведено под каждую из этих культур?
Решить систему уравнений: у – 2х = 4, 7х – у = 1.
Помоги себе сам!
Слайд 6
х- девочек, у – мальчиков;
х+у=25;
2х+3у=63.
Ответ:
2. х – кроликов, у – кур;
х+у=20;
4х +2у=52.
Ответ:6 кроликов,14 кур.
х – легковых, у – грузовых
х +у = 22,
у – х = 8.
Ответ: 7 легковых, 15 грузовых.
х – гречиха, у – просо
х + у = 19,
х – у = 5.
Ответ: 7 га проса, 12 га гречихи.
5. Ответ: х = 1, у = 6.
Проверь себя
Слайд 7Применяя графические представления, выясните сколько решений имеет система уравнений:
ху = 1,
Слайд 9Применяя графические представления, выясните сколько решений имеет система уравнений:
ху = -2,
Слайд 11Применяя графические представления, выясните сколько решений имеет система уравнений:
у = х,
Слайд 13Применяя графические представления, выясните сколько решений имеет система уравнений:
у = х³,
Слайд 15Применяя графические представления, выясните сколько решений имеет система уравнений:
У = √х,
Слайд 17Применяя графические представления, выясните сколько решений имеет система уравнений:
У = х³,
Слайд 19Применяя графические представления, выясните сколько решений имеет система уравнений:
(х – 5)²
Слайд 21Применяя графические представления, выясните сколько решений имеет система уравнений:
У = 2х
Слайд 23
Биллион – миллиард.
Близнецы – два простых числа с разностью, равной 2.
В первой сотне 8 пар близнецов: (3;5),(5;7), (11;13). (17;19), (29;31), (41;43), (59;61), (71;73).
Дружественные числа – натуральные числа А и В такие, что А есть сумма всех натуральных делителей числа В, меньших В, а число В есть сумма всех натуральных делителей числа А, меньших А.
Первая пара дружественных чисел (220; 284).
220 = 1 + 2 +4 + 71 + 142;
284 = 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110
Была известна древнегреческому учённому Пифагору (6 век до н.э.)
Интересно знать?
Слайд 24
Гипотенуза прямоугольного треугольника равна 20 сантиметрам. Найдите его катеты, если один
Площадь прямоугольника равна 56 сантиметрам квадратным, а разность сторон 10 сантиметрам. Вычислите стороны прямоугольника.
Решить систему уравнений:
2х + у = 12, 7х – 2у= 31.
Помощь друга!
Слайд 25
Прямоугольный треугольник.
Гипотенуза – 20 см.
Катеты: х, у;
Один из катетов на 4
Теорема Пифагора:
х² +у² = 400
Система уравнений:
х – у = 4, х² + у² = 400.
Ответ: катеты – 12 см., 16 см.
Прямоугольник.
а,в – стороны пр-ка;
Разность сторон: а - в=10;
Площадь: а . в=56.
Система уравнений:
а – в = 10, а . в = 56.
Ответ: стороны – 4см., 14 см.
Ответ: х= 5, у = 2.
Проверь себя!
Слайд 26
Пятый член арифметической прогрессии равен 8,4, а её десятый член равен
Найдите сумму первых восьми членов геометрической прогрессии, второй член которой равен 6, а четвёртый равен 24.
Решить систему уравнений:
х + у = 6, 3х – 5у =2.
Слово лидеру!
Слайд 27Проверь себя!
Арифметическая прогрессия: пятнадцатый член = 20,4.
Геометрическая прогрессия: сумма первых восьми
Ответ:
Слайд 28
Решите системы уравнений из сборника заданий для подготовки к итоговой аттестации:
Повторить «Решение неравенств» и «Решение систем неравенств».
Домашнее задание.