с одной переменной.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Решение неравенств с одной переменной. Решение систем неравенств с одной переменной. (8 класс)
Содержание
- 1. Презентация по математике на тему: Решение неравенств с одной переменной. Решение систем неравенств с одной переменной. (8 класс)
- 2. Математику нельзя изучать, наблюдая как это делает сосед.
- 3. Разработано учителем
- 4. Цель урока:Научить решать простые неравенства с одной
- 5. Ход урока:Проверка домашнего задания (около доски без
- 6. 1 Вариант №1. Найдите наименьшее целое
- 7. 2 Вариант №1. Найти наибольшее целое число
- 8. Неравенства бывают: линейные
- 9. Вспомним:
- 10. Изобразите на координатной прямой промежуток
- 11. Линейные неравенстваОпределения:Запись вида а>в; а≥в или ав, а
- 12. Линейные неравенстваПравила:1) Если из одной части неравенства
- 13. Линейные неравенстваПравила:2) Обе части неравенства можно умножить
- 14. Линейные неравенстваПравила: 3) Обе части неравенства можно
- 15. Решим неравенство: 16х>13х+45Решение: 16х-13х > 45
- 16. Решить неравенство: 2х + 4 ≥ 6
- 17. Решить неравенства в парах:
- 18. Проверим:х+2 ≥ 2,5х-1Решение: х-2,5х ≥ -2 -1
- 19. Самостоятельная работа по вариантам: решить неравенстваВариант 1.1) 3х≤212) -5х145) 3-9х≤1-х6) 5(х+4)163) 5х+11≥14) 3-2х2(5х-7)
- 20. Проверим ответы:Вариант 1. 1) (-∞;7]
- 21. Оценки
- 22. Самостоятельная работа Найдите наименьшее целое число,
- 23. Проверим:1) 2(х-3)-1-3(х-2)-4(х+1) < 0 2х -6-1-3х+6-4х-4 <
- 24. Решаем сами: Найдите наименьшее натуральное число, являющееся
- 25. Зарядка для ума – устный счет Укажите
- 26. Повторение: Какие неравенства соответствуют промежуткам: а) [0;+∞);
- 27. Ответ:
- 28. Для самых быстрых: Если вы волновались, я
- 29. Решение: 1) пусть х – масса одной
- 30. Спасибо за внимание! Успехов!
- 31. КВАДРАТНЫЕНЕРАВЕНСТВА(8 класс)
- 32. Математику нельзя изучать, наблюдая как это делает сосед.
- 33. Квадратные неравенстваОпределение: Квадратным называетсянеравенство, левая часть которого
- 34. Решением неравенства с одним неизвестным называется
- 35. Являются ли следующие неравенства квадратными? А)
- 36. Основные способы решения квадратных неравенств:Метод интерваловГрафический метод
- 37. Запомним:Чтобы решить квадратное неравенство ах²+вх+с >0 методом
- 38. Решим квадратное неравенство методом интервалов:Дано неравенство: х²
- 39. Работаем в парах:Решить неравенства: 1)
- 40. Решите неравенства методом интервалов самостоятельно:Решить неравенства
- 41. Графический метод решения квадратного неравенства:1).Определить направление ветвей
- 42. Например:Решить графически неравенство х²+5х-6≤0Решение: рассмотрим у
- 43. Решите графически неравенства в парах:1) х²-3х0;3) х²+2х≥0;4) -2х²+х+1≤0Проверим ответы:(0;3)(-∞;0)U(4;+∞)(-∞; -2]U[0; +∞)(-∞; - 0,5]U[1; +∞)
- 44. ВсемСПАСИБО ЗА УРОК!!!
- 45. Источники изображенийhttp://www.istina.org/Video/Glbs.JPGhttp://www.ufps.kamchatka.ru/uploads/news/school_/Colorful%20notebooks%20and%20pen.jpghttp://88.198.21.149/images/photoframes/2010/6/02/17/55/ZkYjfVBHuYRh97SNf65.jpghttp://psychology.careeredublogs.com/files/2010/02/school.jpg
Математику нельзя изучать, наблюдая как это делает сосед.
Слайд 3
Разработано учителем
математики
МБОУ «Янгорчинская СОШ»
Вурнарского района
Корниловым Дмитрием Яковлевичем
МБОУ «Янгорчинская СОШ»
Вурнарского района
Корниловым Дмитрием Яковлевичем
Слайд 4Цель урока:
Научить решать простые неравенства с одной переменной;
Повторить и обобщить знания
учащихся по теме «Неравенства с одной переменной»;
Развивать навыки коллективной работы, взаимопомощи, самоконтроля.
Развивать навыки коллективной работы, взаимопомощи, самоконтроля.
Слайд 5Ход урока:
Проверка домашнего задания (около доски без тетради).
Повторение определений и свойств
неравенств.
Выполнение упражнений.
Самостоятельная работа.
Закрепление изученного материала.
Итоги урока (самостоятельная работа, активное участие).
Задание на дом по карточкам.
Выполнение упражнений.
Самостоятельная работа.
Закрепление изученного материала.
Итоги урока (самостоятельная работа, активное участие).
Задание на дом по карточкам.
Слайд 6 1 Вариант №1. Найдите наименьшее целое число х, удовлетворяющее неравенству: а) х≥-24;
б) х > 4; в) х ≥ -5,9. Ответ: а) -24; б) 3; в) -5.
№2. Решите неравенство: а) 2 – х> х+18; б)5х + 1 < 3x – 2. Ответ: а)(-∞;1/3); б) (-∞;-1,5).
№3. Решите неравенство и изобразите множество его решений на числовой оси: а) 2 – х > х+18; б) (х-1)/2 - 3х>(3х +15)/2.
Ответ: а) (-∞;-8) ; б) (-∞;-2).
Слайд 72 Вариант №1. Найти наибольшее целое число х, удовлетворяющее неравенству: а) х
≤-14; б) х < 24; в) х ≤ -4,1.
Ответ: а) -14; б) 23; в) -5.
№2. Решите неравенство: а) 1 – х>2(х+8);
б) 4х – 1<х +2.
Ответ: а) (-∞;-5); б) (-∞;1).
№3. Решите неравенство и изобразите множество его решений на числовой оси: а) 2 – 5х >х +20; б) (х-1)/2 – 3х/2 >(3х+19)/2.
Ответ: а)(-∞;-18); б) (-∞;-4).
Слайд 10
Изобразите на координатной прямой промежуток
(работаем в парах):
1) [-2;4]
2) (-3;3)
3) (3;+∞)
4) (-∞;4]
5) (-5;+∞)
6) (0;7]
3) (3;+∞)
4) (-∞;4]
5) (-5;+∞)
6) (0;7]
а) х≥2
в) х≤3
с) х>8
д) х<5
е) -4<х<7
ж) -2≤х<6
![Изобразите на координатной прямой промежуток (работаем в парах): 1) [-2;4] 2) (-3;3)](/img/thumbs/84fa028d0f815cad42ed881a9fb2b58e-800x.jpg "Презентация по математике на тему: Решение неравенств с одной переменной. Решение систем неравенств с одной переменной. (8 класс) Изобразите на координатной прямой промежуток (работаем в парах): 1) [-2;4]")
Слайд 11Линейные неравенства
Определения:
Запись вида а>в; а≥в или а
а≥в, а≤в называются
нестрогими.
Неравенства вида а>в, а<в называются
строгим
4) Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.
нестрогими.
Неравенства вида а>в, а<в называются
строгим
4) Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство.
Слайд 12Линейные неравенства
Правила:
1) Если из одной части неравенства перенести в другую слагаемые
с противоположным знаком, то получится равносильное ему неравенства.
Слайд 13Линейные неравенства
Правила:
2) Обе части неравенства можно умножить или разделить на одно
и тоже положительное число, то получится равносильное ему неравенство.
Слайд 14Линейные неравенства
Правила:
3) Обе части неравенства можно умножить или разделить на
одно и тоже отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
Слайд 15Решим неравенство: 16х>13х+45
Решение:
16х-13х > 45 слагаемое
13х с противоположным знаком
перенесли в левую часть неравенства
3х > 45 привели подобные слагаемые
х > 15 поделили обе части неравенства на 3
15 х
Ответ: (15;+∞)
перенесли в левую часть неравенства
3х > 45 привели подобные слагаемые
х > 15 поделили обе части неравенства на 3
15 х
Ответ: (15;+∞)
Слайд 18Проверим:
х+2 ≥ 2,5х-1
Решение:
х-2,5х ≥ -2 -1
- 1,5х ≥
- 3
х ≤ 2
2 х
Ответ: (-∞;2]
х ≤ 2
2 х
Ответ: (-∞;2]
2) х²+х < х(х-5)+2
Решение:
х²+х < х²- 5х +2
х² +х - х²+5х < 2
6х < 2
х < ⅓
⅓ х
Ответ: (-∞;⅓)
Слайд 19Самостоятельная работа по вариантам: решить неравенства
Вариант 1.
1) 3х≤21
2) -5х14
5)
3-9х≤1-х
6) 5(х+4)<2(4х-5)
6) 5(х+4)<2(4х-5)
Вариант 2.
1) 2х≥18
2) -4х>16
3) 5х+11≥1
4) 3-2х<-1
5) 17х-2≤12х-1
6) 3(3х-1)>2(5х-7)
Слайд 20Проверим ответы:
Вариант 1.
1) (-∞;7]
2) (7;∞)
3) (-∞;-1]
4) (-∞;-2)
5) [0,25;∞)
6) (10;∞)
4) (-∞;-2)
5) [0,25;∞)
6) (10;∞)
Вариант 2.
1) [9;∞)
2) (-∞;-4)
3) [-2;∞)
4) (2;∞)
5) (-∞;0,5]
6) (-∞;9)
![Проверим ответы:Вариант 1. 1) (-∞;7] 2) (7;∞) 3) (-∞;-1]](/img/thumbs/48c074c79fcee434211c7f934f2e4611-800x.jpg "Презентация по математике на тему: Решение неравенств с одной переменной. Решение систем неравенств с одной переменной. (8 класс) Проверим ответы:Вариант 1. 1) (-∞;7] 2) (7;∞) 3)")
Слайд 22Самостоятельная работа
Найдите наименьшее целое число, являющееся решением неравенства:
1) 2(х-3)-1-3(х-2)-4(х+1) < 0;
2) 0,2(2х+2)-0,5(х-1)<2
2) 0,2(2х+2)-0,5(х-1)<2
Слайд 23Проверим:
1)
2(х-3)-1-3(х-2)-4(х+1) < 0
2х -6-1-3х+6-4х-4 < 0
-5х < 5
х > -1
-1 х
Ответ: 0
х > -1
-1 х
Ответ: 0
2)
0,2(2х+2)-0,5(х-1)<2 0,4х +0,4 -0,5х +0,5 <2
-0,1х < -0,9 +2
-0,1х < +1,1
х > 11
11 х
Ответ: 12
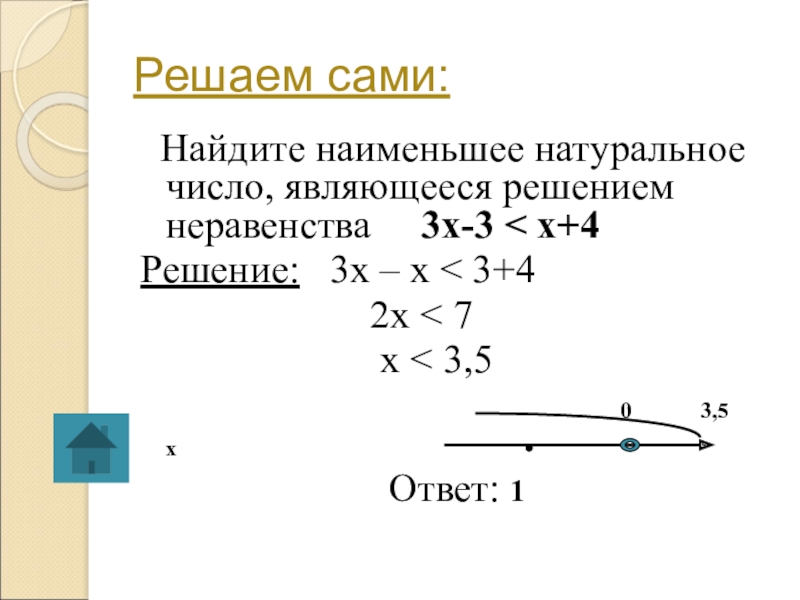
Слайд 24Решаем сами:
Найдите наименьшее натуральное число, являющееся решением неравенства
3х-3 < х+4
Решение: 3х – х < 3+4
2х < 7
х < 3,5
0 3,5 х
Ответ: 1
Решение: 3х – х < 3+4
2х < 7
х < 3,5
0 3,5 х
Ответ: 1
Слайд 25Зарядка для ума – устный счет Укажите все целые числа, принадлежащие промежутку
[-4;4].
Укажите какое – либо число из промежутка (3,5; 3,6).
Принадлежит ли промежутку [8;41] число 40,9?
![Зарядка для ума – устный счет Укажите все целые числа, принадлежащие промежутку [-4;4]. Укажите какое – либо](/img/thumbs/32e5b01c4f464c4eebe8bf4fad28047f-800x.jpg "Презентация по математике на тему: Решение неравенств с одной переменной. Решение систем неравенств с одной переменной. (8 класс) Зарядка для ума – устный счет Укажите все целые числа, принадлежащие")
Слайд 26Повторение: Какие неравенства соответствуют промежуткам: а) [0;+∞); б) (-∞;5);
в) [-3;5); г) (-∞;-5].
1) x<5; 2) x≥0; 3) x≤-5; 4) -3≤x<5;
Слайд 28Для самых быстрых: Если вы волновались, я посоветую вам принимать успокоительный чай.
Рецепт успокоительного чая:
Трава пустырника – 6 частей;
Шишки хмеля – 3 части;
Листья мяты – 2 части;
Корень валерианы – 4 части;
Всего – 300 грамм.
Посчитайте, сколько граммов надо взять каждого вещества.
Слайд 29Решение: 1) пусть х – масса одной части, тогда можно составить уравнение:
6х + 3х + 2х + 4х =300;
15х = 300;
х = 20;
20 *6 = 120 (г) – пустырника
20 * 3 = 60 (г) – хмеля
20 *2 =40 (г) – мяты
20 * 4 = 80 (г) валерианы
Слайд 33Квадратные неравенства
Определение: Квадратным называется
неравенство, левая часть которого −
квадратный трёхчлен, а правая
часть
равна нулю:
ах²+bх+с>0 ах²+bх+с≥0
ах²+bх+с<0 ах²+bх+с≤0
равна нулю:
ах²+bх+с>0 ах²+bх+с≥0
ах²+bх+с<0 ах²+bх+с≤0
Слайд 34
Решением неравенства с одним неизвестным называется то значение неизвестного, при
котором это неравенство обращается в верное числовое неравенство
Решить неравенство − это значит найти все его решения или установить, что их нет.
Решить неравенство − это значит найти все его решения или установить, что их нет.
Слайд 35Являются ли следующие неравенства квадратными?
А) 4у² - 5у +7
> 0
Б) 2х - 4 > 0
В) 4х² - 2х ≥ 0
Г) 3у – 5у² + 7 < 0
Д) 4 – 6х + 5х² ≤ 0
Е) 5у⁴ +3у - 6 < 0
Б) 2х - 4 > 0
В) 4х² - 2х ≥ 0
Г) 3у – 5у² + 7 < 0
Д) 4 – 6х + 5х² ≤ 0
Е) 5у⁴ +3у - 6 < 0
Слайд 37Запомним:
Чтобы решить квадратное неравенство ах²+вх+с >0 методом интервалов надо:
1) Найти корни
соответствующего
квадратного уравнения ах²+вх+с = 0;
2) Корни уравнения нанести на числовую ось;
3) Разделить числовую ось на интервалы;
3) Определить знаки функции в каждом из интервалов;
4) Выбрать подходящие интервалы и
записать ответ.
квадратного уравнения ах²+вх+с = 0;
2) Корни уравнения нанести на числовую ось;
3) Разделить числовую ось на интервалы;
3) Определить знаки функции в каждом из интервалов;
4) Выбрать подходящие интервалы и
записать ответ.
Слайд 38Решим квадратное неравенство методом интервалов:
Дано неравенство: х² + х – 6
≥ 0
Решение: 1) решим соответствующее квадратное уравнение х² + 5х – 6 = 0.
Т.к. а+в+с=0, то х₁ =1, а х₂ = - 6
2)
-6 1 х
3) Запишем ответ:
(-∞; -6]U[1; +∞)
Решение: 1) решим соответствующее квадратное уравнение х² + 5х – 6 = 0.
Т.к. а+в+с=0, то х₁ =1, а х₂ = - 6
2)
-6 1 х
3) Запишем ответ:
(-∞; -6]U[1; +∞)
+
+
-
Слайд 39Работаем в парах:
Решить неравенства:
1) х²-3х
х²-4х>0;
3) х²+2х≥0;
4) -2х²+х+1≤0
3) х²+2х≥0;
4) -2х²+х+1≤0
Проверим ответы:
(0;3)
(-∞;0)U(4;+∞)
(-∞; -2]U[0; +∞)
(-∞; - 0,5]U[1; +∞)
Слайд 40
Решите неравенства методом интервалов самостоятельно:
Решить неравенства
1) х(х+7)≥0;
2) (х-1)(х+2)≤0;
3) х- х²+2<0;
4) -х²-5х+6>0;
5) х(х+2)<15
4) -х²-5х+6>0;
5) х(х+2)<15
Проверим ответы:
1) (-∞;-7]U[0; +∞)
2) [-2;1]
3) (-∞;-1)U(2; +∞)
4) (-6;1)
5) (-5;3)
Слайд 41Графический метод решения квадратного неравенства:
1).Определить направление ветвей параболы, по знаку первого
коэффициента квадратичной функции.
2).Найти корни соответствующего квадратного уравнения;
3). Построить эскиз графика и по нему
определить промежутки, на которых
квадратичная функция принимает
положительные или отрицательные
значения
2).Найти корни соответствующего квадратного уравнения;
3). Построить эскиз графика и по нему
определить промежутки, на которых
квадратичная функция принимает
положительные или отрицательные
значения
Слайд 42Например:
Решить графически неравенство х²+5х-6≤0
Решение: рассмотрим у = х²+5х-6,
это квадратичная функция, графиком является парабола, т.к. а=1, то ветви направлены вверх.
у
+ +
-6 1 x
Ответ: [-6;1]
у
+ +
-6 1 x
Ответ: [-6;1]
-
Слайд 43Решите графически неравенства
в парах:
1) х²-3х0;
3) х²+2х≥0;
4) -2х²+х+1≤0
Проверим ответы:
(0;3)
(-∞;0)U(4;+∞)
(-∞; -2]U[0; +∞)
(-∞;
- 0,5]U[1; +∞)
![Решите графически неравенства в парах:1) х²-3х0;3) х²+2х≥0;4) -2х²+х+1≤0Проверим ответы:(0;3)(-∞;0)U(4;+∞)(-∞; -2]U[0; +∞)(-∞; - 0,5]U[1; +∞)](/img/thumbs/469c29420b7cf4f4565f782231c5af07-800x.jpg "Презентация по математике на тему: Решение неравенств с одной переменной. Решение систем неравенств с одной переменной. (8 класс) Решите графически неравенства в парах:1) х²-3х0;3) х²+2х≥0;4) -2х²+х+1≤0Проверим ответы:(0;3)(-∞;0)U(4;+∞)(-∞; -2]U[0; +∞)(-∞; - 0,5]U[1; +∞)")
Слайд 45Источники изображений
http://www.istina.org/Video/Glbs.JPG
http://www.ufps.kamchatka.ru/uploads/news/school_/Colorful%20notebooks%20and%20pen.jpg
http://88.198.21.149/images/photoframes/2010/6/02/17/55/ZkYjfVBHuYRh97SNf65.jpg
http://psychology.careeredublogs.com/files/2010/02/school.jpg
