- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Производные
Содержание
- 1. Презентация по математике на тему Производные
- 2. Методы исследования:Изучение исторического материалаИзучение учебного, научного материалаИзучение Интернет - ресурсов
- 3. Цель: Расширить знание о применении теории производной в предметах школьного курса
- 4. Актуальность Данная работа актуальна и своевременна
- 5. Практическое применение производной «…нет ни одной
- 6. ПроизводнаяТема «Производная» - это одна из важнейших
- 7. «Дифференциальное исчисление- это описание окружающего нас мира,
- 8. ГипотезаКак можно использовать знания, связанные с производной, в практической жизни
- 9. Из истории Термин «производная» – это буквальный
- 10. Слайд 10
- 11. О великом Ньютоне! Был этот
- 12. Г.В. Лейбниц
- 13. Николо ТартальяФормула производной встречается ещё в 15
- 14. Рене ДекартРоберьвальБарроуПроизводная и различные изложения с её
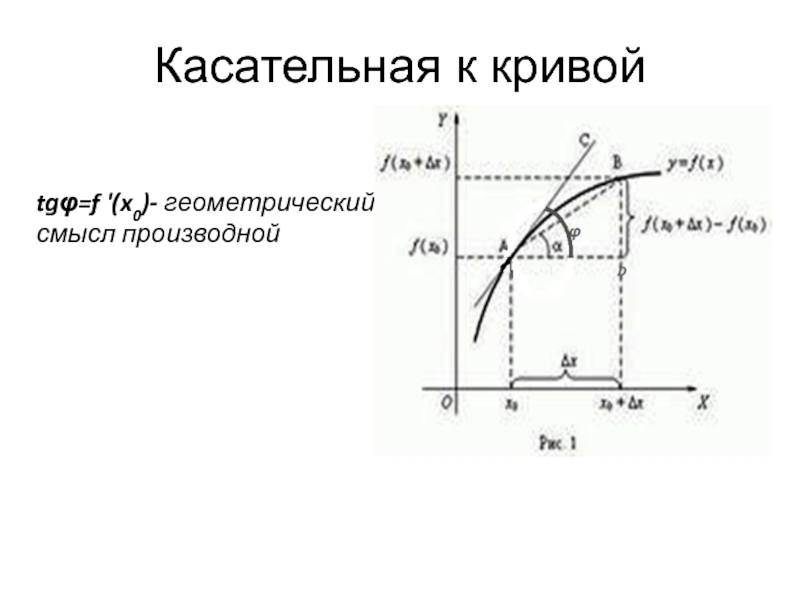
- 15. Касательная к кривойtgφ=f '(x0)- геометрический смысл производной
- 16. Некоторая функция f(x) задана графически. На кривой
- 17. Физический смысл производнойФизический смысл производной заключается в
- 18. В математике производная характеризует крутизну графика, в
- 19. ПРОИЗВОДНАЯ В АЛГЕБРЕРешить уравнение:Рассмотрим функциюНайдем наибольший общий
- 20. ПРОИЗВОДНАЯ В ХИМИИ И БИОЛОГИИ
- 21. Задача по биологии: По известной зависимости
- 22. Популяция – это совокупность особей данного вида,
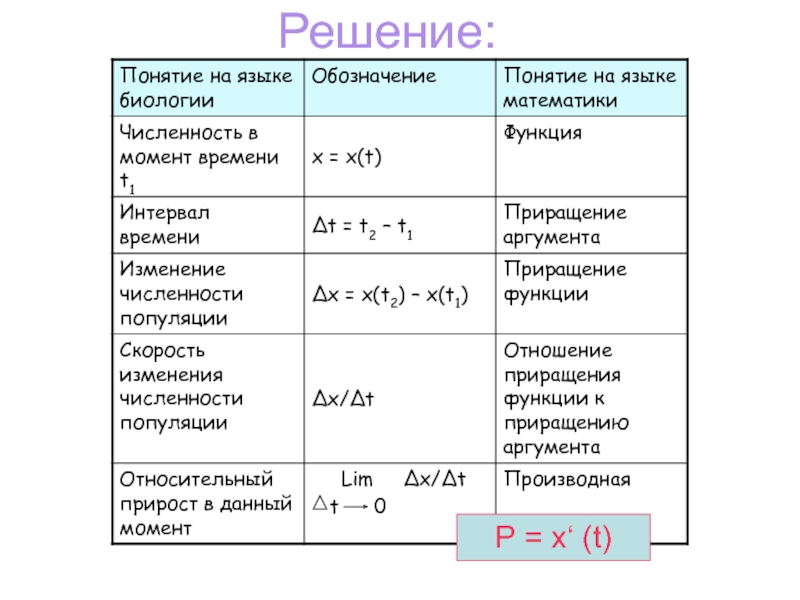
- 23. Решение:Р = х‘ (t)
- 24. Задача по химии: Пусть количество вещества,
- 25. V (t) = p ‘(t)Решение:
- 26. Применение производной в физике
- 27. Мощность – это производная работы по времени
- 28. Задача. Вычислить количество теплоты, которое необходимо для
- 29. Решение Пусть Q=Q(t).Рассмотрим малый отрезок [t; t+Δt],
- 30. ЗарядЗадача. Вычислить силу тока I, который несет
- 31. РешениеРассмотрим приращение заряда на маленьком отрезке [t;
- 32. Применение производной в географии
- 33. Задача :Вывести формулу для вычисления численности населения
- 34. Решение:Пусть у=у(t)- численность населения.Рассмотрим прирост населения за
- 35. Численность населения в с. ТрехбалтаевоКр =16,Кс =30, К = -14, тогда численность - 2080 человек
- 36. Производная и ее связь с экономикойПроизводной от функции у
- 37. Производная решает важные вопросы.В каком направлении изменится
- 38. Производительность трудаЧерез производную можно определить производительность труда:Пусть функция u
- 39. Задача по экономической теории.Предприятие производит Х единиц
- 40. Заключение Применение математической теории к решению
- 41. ЛитератураТерешин Н.А., Терешина Т.Н. «2000 задач по
- 42. Спасибо за внимание!
- 43. Ряд задач дифференциального исчисления был решен еще
Слайд 1
Исследовательская работа
Практическое применение производной
Руководитель: Стратилатова Полина
Викторовна, учитель
математики
МБОУ «Трехбалтаевская СООШ»
2014-2015
Слайд 2Методы исследования:
Изучение исторического материала
Изучение учебного, научного материала
Изучение Интернет - ресурсов
Слайд 4Актуальность
Данная работа актуальна и своевременна для развития познавательного интереса
Слайд 5Практическое применение производной
«…нет ни одной области в математике, которая
не окажется применимой к явлениям
действительного мира…»
Н.И. Лобачевский
Слайд 6Производная
Тема «Производная» - это одна из важнейших тем курса математического анализа,
Слайд 7«Дифференциальное исчисление- это описание окружающего нас мира, выполненное на математическом языке.
Слайд 9Из истории
Термин «производная» – это буквальный перевод на русский derivee. Этот
Слайд 10 Честь открытия основных законов
Их, великих, загадочность окружающего мира притягивала, а исследование увлекало.
Слайд 11О великом Ньютоне!
Был этот мир глубокой тьмой окутан.
А.Поуг.
Исаак Ньютон (1643-1727) - один из создателей дифференциального исчисления.
Главный его труд- «Математические начала натуральной философии»-оказал колоссальное влияние на развитие естествознания, стал поворотным пунктом в истории естествознания.
Ньютон ввёл понятие производной, изучая законы механики, тем самым раскрыл её механический смысл.
Слайд 12Г.В. Лейбниц
(1646-1716)
символики математического анализа.
Лейбниц пришёл к понятию производной решая задачу проведения касательной к произвольной линии, объяснив этим ее геометрический смысл .
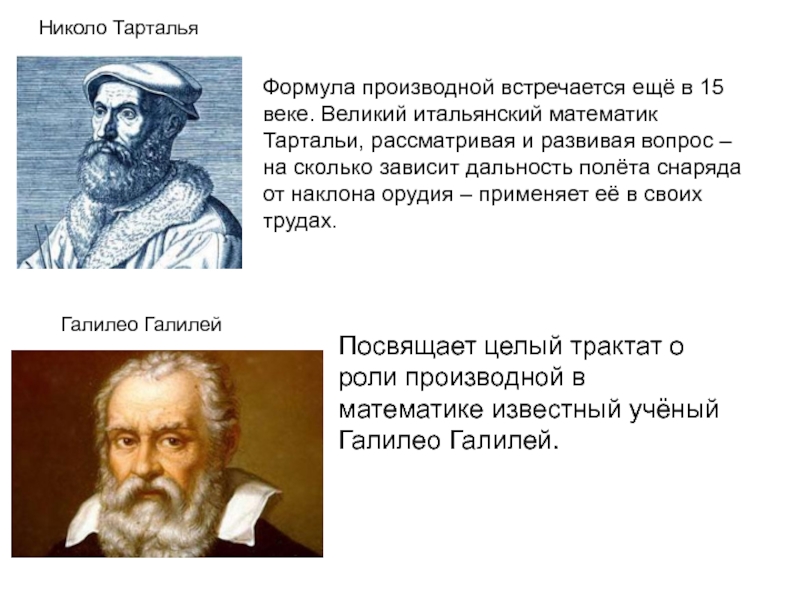
Слайд 13Николо Тарталья
Формула производной встречается ещё в 15 веке. Великий итальянский математик
Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей.
Галилео Галилей
Слайд 14Рене Декарт
Роберьваль
Барроу
Производная и различные изложения с её применением встречаются в работах
Слайд 16Некоторая функция f(x) задана графически. На кривой возьмем точку А с
Δх - малая величина. Если точку В двигать по кривой к точке А, то есть Δх?0, то секущая АВ переходит в касательную АС. Предельное отношение Δf /Δх – это будет производной в точке x0.
Отношение Δf /Δх в треугольнике АВD – это отношение противолежащего катета к прилежащему катету, то есть tgα.
α мало отличается от угла φ, поэтому tgα = tgφ = f '(x0). То есть тангенс угла наклона касательной к оси ОХ – это производная в точке х0. Таким образом мы получили геометрический смысл производной.
Слайд 17Физический смысл производной
Физический смысл производной заключается в скорости изменения функции.
Пусть s=s(t)
Слайд 18В математике производная характеризует крутизну графика, в механике – скорость неравномерного
Производная в разных предметах школьного курса
Слайд 19ПРОИЗВОДНАЯ В АЛГЕБРЕ
Решить уравнение:
Рассмотрим функцию
Найдем наибольший общий делитель
и
.
и
Корень х=1 –
Значит f(x) делится на (х-1)^2. Разделив, получаем
Ответ: х1=х2= 1, х3=6.
Слайд 21Задача по биологии:
По известной зависимости численности популяции x (t)
в момент времени t.
Слайд 22Популяция – это совокупность особей данного вида, занимающих определённый участок территории
Слайд 24Задача по химии:
Пусть количество вещества, вступившего в химическую реакцию
р(t) = t2/2 + 3t –3 (моль)
Найти скорость химической реакции через 3 секунды.
Ответ: 6
Слайд 27Мощность – это производная работы по времени P = A' (t).
Сила
Сила – есть производная работы по перемещению F = A' (x).
Теплоемкость – это производная количества теплоты по температуре C = Q' (t).
Давление – производная силы по площади P = F'(S)
При изучении изменяющихся величин очень часто возникает вопрос о скорости, о быстроте происходящего изменения. Так мы говорим о скорости движения самолета, поезда, автобуса, ракеты, о скорости падения камня, вращения шкива и т.д. Можно говорить о скорости выполнения определенной работы, о скорости протекания химической реакции, о быстроте роста населения в данном городе. О скорости можно говорить по отношению к любой величине, которая изменяется с течением времени. Для всего этого используется понятие производной.
Слайд 28Задача. Вычислить количество теплоты, которое необходимо для того, чтобы нагреть 1
Теплота
Слайд 29Решение
Пусть Q=Q(t).
Рассмотрим малый отрезок [t; t+Δt],
на этом отрезке
ΔQ=c(t)
c(t)= ΔQ/Δt
При Δt→0 lim ΔQ/Δt =Q′(t)
Δt→0
c(t)=Q′(t)
Слайд 30Заряд
Задача. Вычислить силу тока I, который несет на себе заряд, заданный
Слайд 31Решение
Рассмотрим приращение заряда на маленьком
отрезке [t; t+Δ t], тогда Δ
Δ q/ Δ t = I(t)
Если Δ t ?0, то lim Δ q/ Δ t = q’(t) ,т.е. I (t)= q’(t)
Δ t?0
I = q’ = -qmw0sinw0t
Слайд 33Задача :
Вывести формулу для вычисления численности населения на ограниченной территории в
Рост численности населения
Слайд 34Решение:
Пусть у=у(t)- численность населения.
Рассмотрим прирост населения за Δt=t-t0
Δy=k y Δt,
кс – коэффициент смертности)
Δy/ Δt=k y
При Δt→0 получим lim Δy/ Δt=у’
у’=к у
Слайд 35Численность населения в с. Трехбалтаево
Кр =16,
Кс =30,
К = -14,
тогда
Слайд 36Производная и ее связь с экономикой
Производной от функции у = f(x) в точке х0 называется предел
Экономика – основа жизни, а в ней важное место
занимает дифференциальное исчисление- аппарат для
экономического анализа. Базовая задача экономического
анализа- изучение связей экономических величин в
виде функций.
Слайд 37Производная решает важные вопросы.
В каком направлении изменится доход государства при увеличении
Увеличится или уменьшится выручка фирмы при повышении цены на ее продукцию?
Для решения этих вопросов нужно построить функции связи входящих переменных , которые затем изучаются методами дифференциального исчисления.
Также с помощью экстремума функции( производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль , максимальный выпуск и минимальные издержки.
Слайд 38Производительность труда
Через производную можно определить производительность труда:
Пусть функция u = u(t) выражает количество
За период времени от tο до tο + Δt количество произведенной продукции изменится от значения uο = u(tο) до значения uο + Δu = u(tο + Δt). Тогда
средняя производительность труда за этот период времени Zср = Δu :Δt. Очевидно, что производительность труда в момент tο можно определить как предельное значение средней производительности за период времени от tο до tο + Δt при Δt → 0, т.е.
z = lim Zср = lim Δu/Δt = u'(t) при Δt→0
Слайд 39Задача по экономической теории.
Предприятие производит Х единиц некоторой однородной продукции в
Функция исследуется с помощью производной. Получаем, что при Х=100 функция достигает максимума.
Вывод: финансовые накопления предприятия растут с увеличением объема производства до 100 единиц, при х =100 они достигают максимума и объем накопления равен 39000 денежных единиц. Дальнейший рост производства приводит к сокращению финансовых накоплений.
Таким образом , задачи ,решаемые с помощью производной, широко используются в производстве.
Слайд 40Заключение
Применение математической теории к решению прикладных задач - это
Слайд 41Литература
Терешин Н.А., Терешина Т.Н. «2000 задач по алгебре и началам анализа.
М.:Аквариум,К.: ГИППВ, 2000. 256 с.Стр.192-193; 216-217; 194; 200; 240.
Виленкин Н.Я. «Функция в природе и технике»: Кн.для внеклас.чтения IX-Xкл. – 2-е изд., испр.–М.: Просвещение,1985. – 192 с. Стр.88; 94.
О.Н. Афанасьева«Сборник задач по математике для техникумов»- М.:Наука 1992.-208 с.Стр.84.
Н.В. Мирошин«Сборник задач с решениями для поступающих в вузы.» - М.: ООО«Издательство Астрель» 2002.-832 с.Стр.496.
Глейзер Г.И. «История математики в школе» - М.:Просвещение,1983 г. Стр. 42.
Волькенштейн В.С. «Сборник задач по общему курсу физики»М., 1979 г.
«Математический энциклопедический словарь.»/Гл.ред.Ю.В.Прохоров.-М:Сов.энциклопедия,1988.-847 с.
«Задачник по курсу математического анализа». ч.II.Под ред. Н.Я.Виленкина.-М:«Просвещение»,1971.
«Задачи и упражнения по математическому анализу для втузов.»/Под ред. Б.П.Демидовича-М: Физматгиз,1963 г. 472 стр.
«Элементы высшей математики»:сб. заданий для практ. занятий:Учеб. Пособие/С.В.Сочнев.-М:Высш.шк., 2003 г.- 192 с.

























![Презентация по математике на тему Производные Решение Пусть Q=Q(t).Рассмотрим малый отрезок [t; t+Δt], на этом отрезке ΔQ=c(t) Решение Пусть Q=Q(t).Рассмотрим малый отрезок [t; t+Δt], на этом отрезке ΔQ=c(t) • Δtc(t)= ΔQ/ΔtПри Δt→0 lim ΔQ/Δt](/img/thumbs/5c5975c4167c512d7dc7887f7a6e39eb-800x.jpg)

![Презентация по математике на тему Производные РешениеРассмотрим приращение заряда на маленьком отрезке [t; t+Δ t], тогда Δ РешениеРассмотрим приращение заряда на маленьком отрезке [t; t+Δ t], тогда Δ q = I(t) Δ t.Δ q/](/img/thumbs/3fe851b59513c693fae1a3be9a5918dc-800x.jpg)

















