- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Применение производной к исследованию функций
Содержание
- 1. Презентация по математике на тему: Применение производной к исследованию функций
- 2. Найдите производные функции: а)y=7x+4
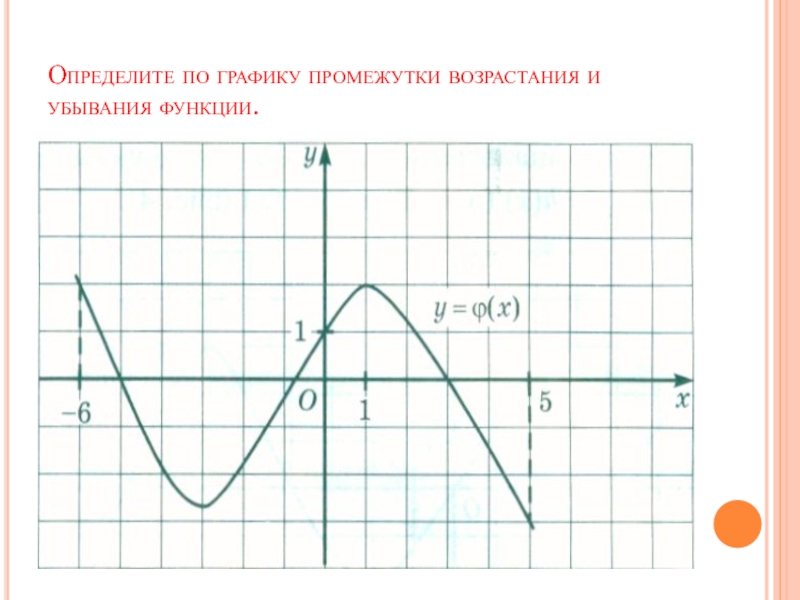
- 3. Определите по графику промежутки возрастания и убывания функции.
- 4. Цель: ознакомиться со способом нахождения промежутков монотонности функции с помощью производной.
- 5. Признаки монотонности функцииДостаточный признак возрастания функции.Если f
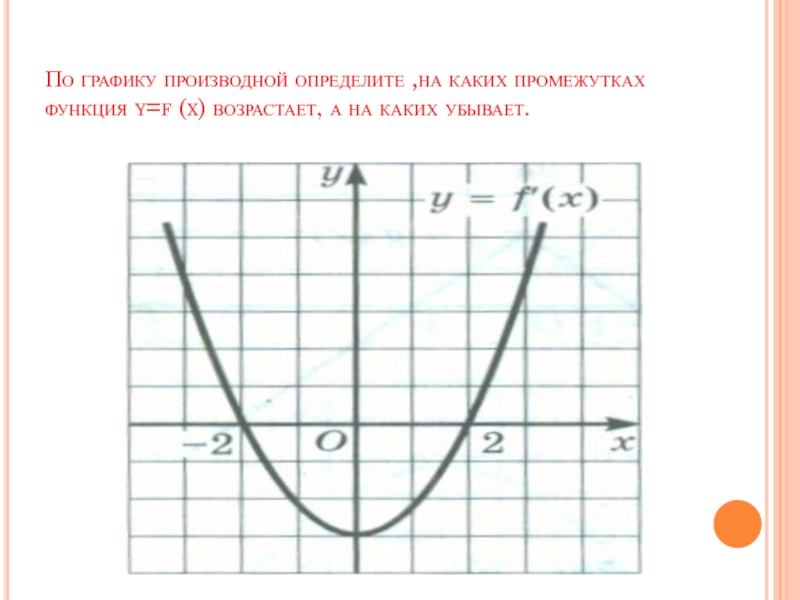
- 6. По графику производной определите ,на каких промежутках функция y=f (x) возрастает, а на каких убывает.
- 7. По графику производной определите ,на каких промежутках
- 8. По графику производной определите ,на каких промежутках функция y=f(x) возрастает, а на каких убывает.
- 9. По графику производной определите ,на каких промежутках
- 10. По графику производной определите ,на каких промежутках функция y=f(x) возрастает, а на каких убывает.
- 11. По графику производной определите ,на каких промежутках
- 12. Слайд 12
- 13. Слайд 13
- 14. Найдите промежутки возрастания и убывания функций.f(x)=3-1/2xРешение: функция
- 15. Найдите промежутки возрастания и убывания функций.f(x)=- X2
- 16. Определите промежутки монотонности функции.Y=x2-5x+4,используя предложенный
- 17. Определите промежутки монотонности функций. Y=x2-5x+4Решение: 1) y
Слайд 2Найдите производные функции:
а)y=7x+4
д)y=cosx е)y=√x̄
ж)y=x5+2x3+1 з)y=x3+1
б) а)y=7x+4 в)y=-6x+1
y=x2 г)y=sinx
Запишите на доске 4правила дифференцирования.
Запишите на доске известные вам формулы дифференцирования.
Слайд 4Цель: ознакомиться со способом нахождения промежутков монотонности функции с помощью производной.
Слайд 5Признаки монотонности функции
Достаточный признак возрастания функции.
Если f ̕(x)>0 в каждой точке
Достаточный признак убывания функции.
Если f ̕(x)<0 в каждой точке интервала U, то функция f(x) убывает на U.
Если f ̕(x)=0 в каждой точке интервала U, то функция f(x) постоянна на U.
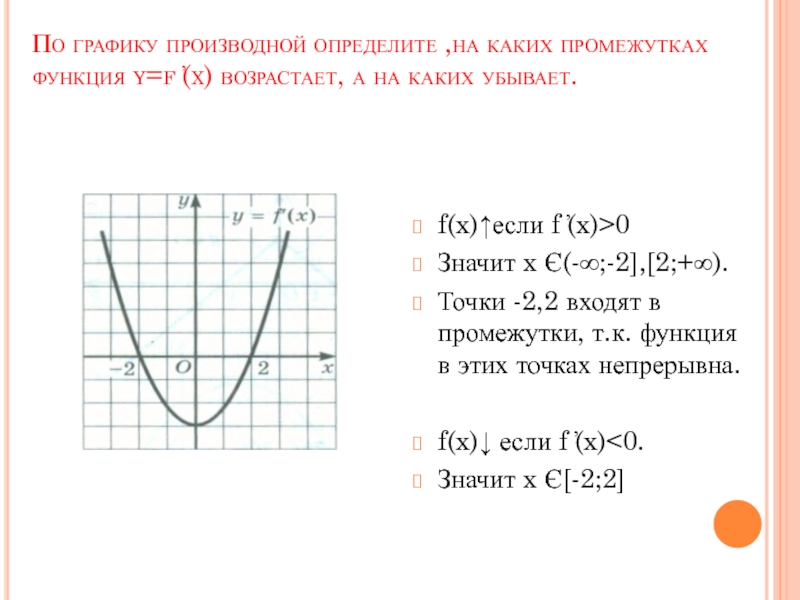
Слайд 6По графику производной определите ,на каких промежутках функция y=f (x) возрастает,
Слайд 7По графику производной определите ,на каких промежутках функция y=f ̕(x) возрастает,
f(x)↑если f ̕(x)>0
Значит x Є(-∞;-2],[2;+∞).
Точки -2,2 входят в промежутки, т.к. функция в этих точках непрерывна.
f(x)↓ если f ̕(x)<0.
Значит x Є[-2;2]
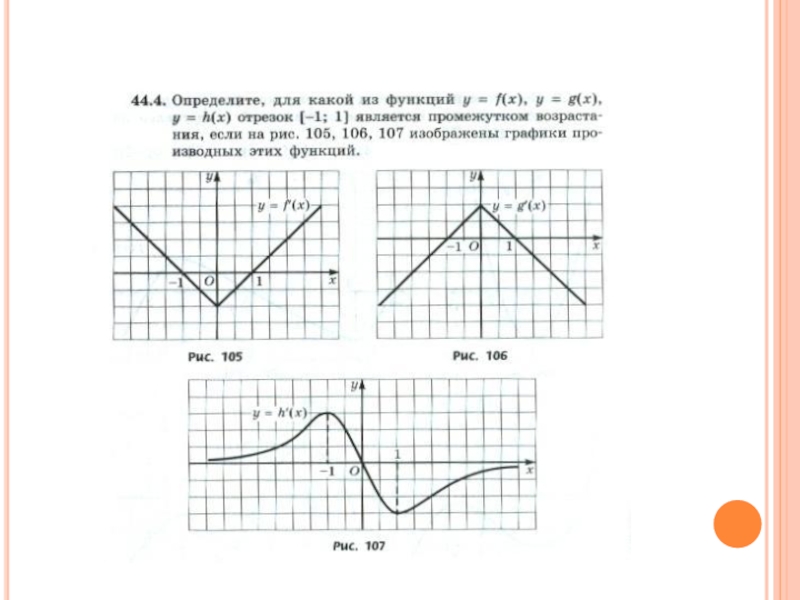
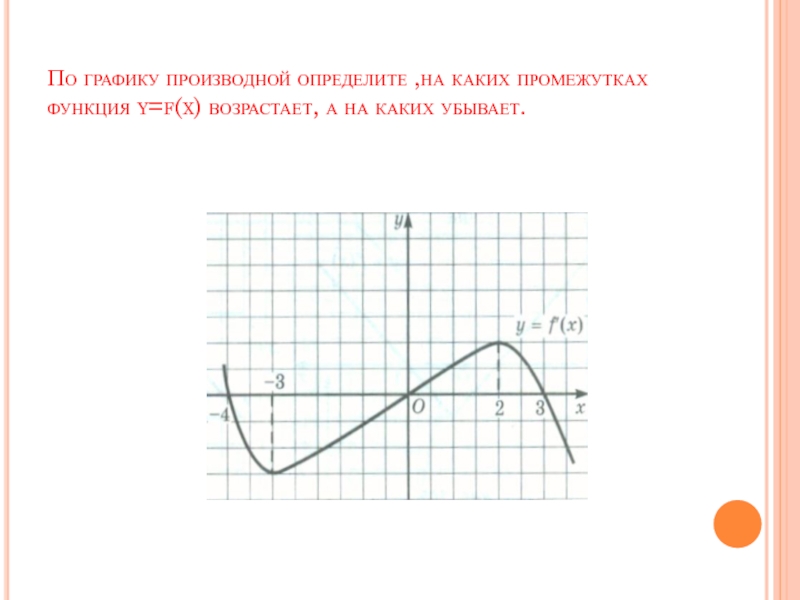
Слайд 8По графику производной определите ,на каких промежутках функция y=f(x) возрастает, а
Слайд 9По графику производной определите ,на каких промежутках функция y=f(x) возрастает, а
f(x)↑если xЄ(-∞;-4],
[0;3] т.к. на этих промежутках f ̕(x)>0
f(x)↓
если xЄ[-4;0],[3;+∞)
т.к. на этих промежутках f ̕(x)<0
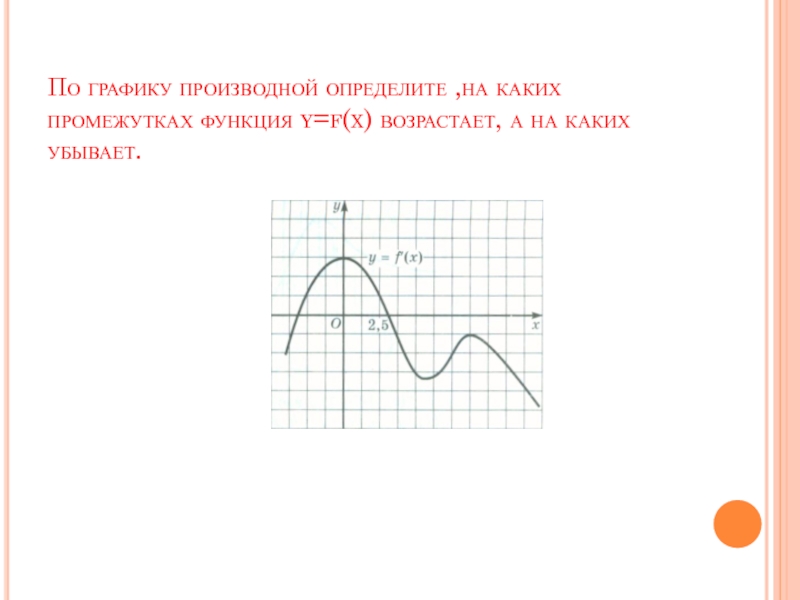
Слайд 10По графику производной определите ,на каких промежутках функция y=f(x) возрастает, а
Слайд 11По графику производной определите ,на каких промежутках функция y=f(x) возрастает, а
f(x)↑если xЄ[-2.5;2.5]
т.к. на этом промежутке f̕ ̕(x)>0
f(x)↓
если xЄ
(- ∞;-2.5],[2.5;+∞)
т.к. на этих промежутках f ̕(x)<0
Слайд 14Найдите промежутки возрастания и убывания функций.
f(x)=3-1/2x
Решение: функция определена на всей числовой
Найдем производную функции:f ̕(x)=-1/2<0, значит функция убывает на промежутке (-∞;+∞).
f(x)=4x-5
Решение: функция определена на всей числовой прямой, т.е. D(f)=(-∞;+∞).
Найдем производную функции:f ̕(x)=4>0 значит функция возрастает на промежутке (-∞;+∞).
Слайд 15Найдите промежутки возрастания и убывания функций.
f(x)=- X2 +2x-3 , D(f)=(-∞;+∞)
f ̕(x)=-2x+2
(точка, в которой производная функции равна 0,
называется стационарной ).
Точка x=1 разбивает область определения функции на 2 интервала (-∞;1) и (1 ;+∞)
Определим знак каждого из интервалов
----+------•---_--------> x=-2,тогда , f ̕(-2)=6>0
1 x=2, тогда f ̕(2)=-2<0
Т.к. функция непрерывна в точке x=1,то 1 можно присоединить к промежуткам.
Ответ: f(x)↑,если xЄ(-∞;1] . f(x)↓ если xЄ [1 ;+∞)
Слайд 16Определите промежутки монотонности функции.
Y=x2-5x+4,используя предложенный
1) Найдите производную функции f (x).
2) Приравняйте ее к нулю и найдите стационарные точки. (f (x)=0)
3) Отметьте стационарные точки на числовой прямой и определите знаки производной на получившихся промежутках.
4) Сделайте выводы о монотонности функции.
Слайд 17Определите промежутки монотонности функций
. Y=x2-5x+4
Решение:
1) y ̕=2x-5,
2) y̕=0,
3) --------•---------->
- 2,5 +
x=2,
f ̕(2)=2*2-5=-1<0
x=3
f ̕(3)=3*3-5=4>0
Ответ:f(x)↓,если x Є(-∞;2,5]
f (x)↑ ,если x Є[2,5;+∞)
Решите самостоятельно №30.12




![Презентация по математике на тему: Применение производной к исследованию функций По графику производной определите ,на каких промежутках функция y=f(x) возрастает, а По графику производной определите ,на каких промежутках функция y=f(x) возрастает, а на каких убывает.f(x)↑если xЄ(-∞;-4],[0;3] т.к. на](/img/thumbs/4ee1aff85486805036b7613d65b70a92-800x.jpg)
![Презентация по математике на тему: Применение производной к исследованию функций По графику производной определите ,на каких промежутках функция y=f(x) возрастает, а По графику производной определите ,на каких промежутках функция y=f(x) возрастает, а на каких убывает.f(x)↑если xЄ[-2.5;2.5] т.к. на](/img/thumbs/fe1a1491643f035afcaad3d8bf7436e0-800x.jpg)