- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Применение производной для исследования функции (10 класс)
Содержание
- 1. Презентация по математике на тему Применение производной для исследования функции (10 класс)
- 2. Разминка
- 3. Разминка№1. Верно ли утверждение:Функция возрастает на [-7;
- 4. Разминка
- 5. Разминка№1. Задан график функции y=f(x).Укажите количество точек
- 6. Разминка
- 7. Разминка№1. Задан график функции y=f '(x).Укажите количество
- 8. Самопроверка№1. -++-+№2. 12112№3. 23122
- 9. Алгоритм построения графика функцииОбласть определения.Чётность, нечётность, периодичность.Точки
- 10. Пример
- 11. 1. Область определения
- 12. 2. Чётность, нечётность, периодичность
- 13. 2. Чётность, нечётность, периодичность
- 14. 3. Точки пересечения с осями координат
- 15. 4. Исследование поведения графика функции на границе области определения
- 16. 5. Точки экстремума. Участки возрастания и убывания функции
- 17. 6. Точки перегиба. Участки выпуклости и вогнутости
- 18. 6. Точки перегиба. Участки выпуклости и вогнутости
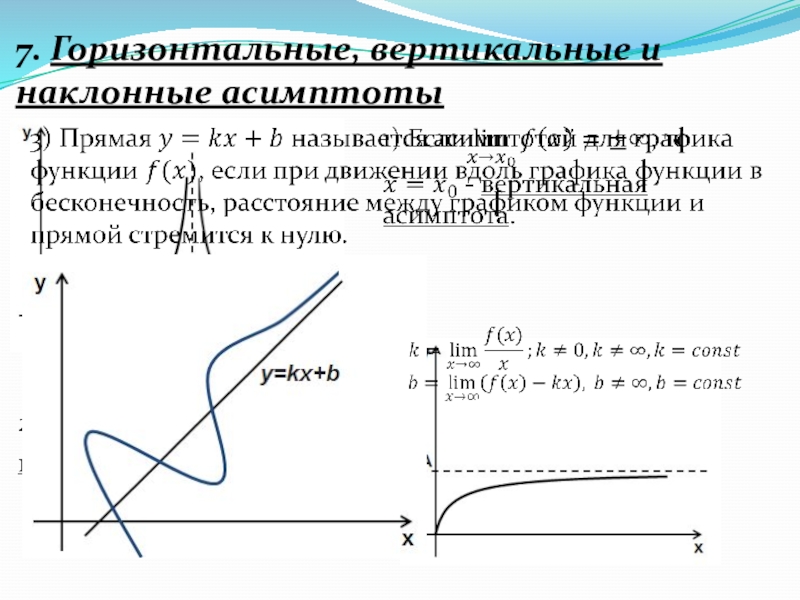
- 19. 7. Горизонтальные, вертикальные и наклонные асимптоты
- 20. 7. Горизонтальные, вертикальные и наклонные асимптоты
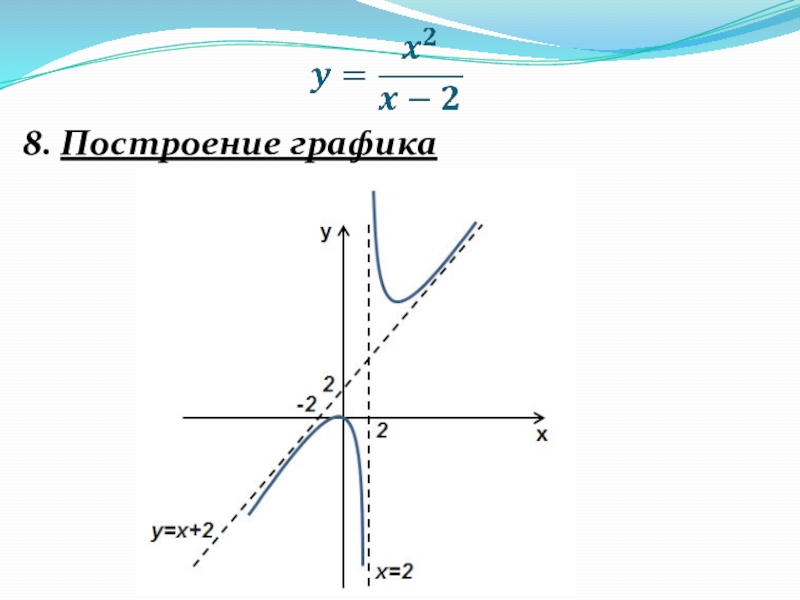
- 21. 8. Построение графика
- 22. Рефлексия
- 23. Домашнее задание
Разминка
Слайд 3Разминка
№1. Верно ли утверждение:
Функция возрастает на [-7; 2) и (2; 8],
значит она возрастает на [-7; 8].
Производная функции в точке x0 равна 0, значит x0 – критическая точка.
Производная функции не существует в точке x0, значит x0 – критическая точка.
Критическая точка является точкой экстремума.
Точка экстремума является критической точкой.
Производная функции в точке x0 равна 0, значит x0 – критическая точка.
Производная функции не существует в точке x0, значит x0 – критическая точка.
Критическая точка является точкой экстремума.
Точка экстремума является критической точкой.
![Разминка№1. Верно ли утверждение:Функция возрастает на [-7; 2) и (2; 8], значит она возрастает на [-7; 8].Производная](/img/thumbs/907a9af043bf9dbdc4399425e50694c2-800x.jpg "Презентация по математике на тему Применение производной для исследования функции (10 класс) Разминка№1. Верно ли утверждение:Функция возрастает на [-7; 2) и (2; 8],")
Слайд 5Разминка
№1. Задан график функции y=f(x).
Укажите количество точек максимума.
Укажите число точек экстремума
Укажите
число точек минимума.
Укажите количество промежутков возрастания.
Укажите количество промежутков убывания.
Укажите количество промежутков возрастания.
Укажите количество промежутков убывания.
Слайд 7Разминка
№1. Задан график функции y=f '(x).
Укажите количество точек максимума.
Укажите число точек
экстремума
Укажите число точек минимума.
Укажите количество промежутков возрастания.
Укажите количество промежутков убывания.
Укажите число точек минимума.
Укажите количество промежутков возрастания.
Укажите количество промежутков убывания.
Слайд 9Алгоритм построения графика функции
Область определения.
Чётность, нечётность, периодичность.
Точки пересечения с осями координат.
Исследование
поведения графика функции на границе области определения.
Точки экстремума, участки возрастания и убывания.
Точки перегиба, участки выпуклости и вогнутости.
Горизонтальные, вертикальные и наклонные асимптоты.
Нанесение данных на координатную плоскость, построение графика.
Точки экстремума, участки возрастания и убывания.
Точки перегиба, участки выпуклости и вогнутости.
Горизонтальные, вертикальные и наклонные асимптоты.
Нанесение данных на координатную плоскость, построение графика.
