- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Применение признаков делимости чисел при решении заданий ЕГЭ
Содержание
- 1. Презентация по математике на тему Применение признаков делимости чисел при решении заданий ЕГЭ
- 2. Слайд 2
- 3. Слайд 3
- 4. Задачи задания 19 можно классифицировать по 4
- 5. Задача 1: Найдите четырехзначное число, кратное 18,
- 6. Решение. abcd :18 → d четное, но d≠0,
- 7. Примеры задач на нахождение числа по данным
- 8. Задача 1. Найдите наименьшее трехзначное натуральное число,
- 9. Примеры задач на нахождение числа вычеркиванием1.
- 10. Задача1. Вычеркните в числе 85417627 три цифры
- 11. Примеры задач на нахождение числа,
- 12. Задача 1. Сумма цифр трёхзначного натурального числа
- 13. Задача 1. Игорь решил сделать домашнее задание
- 14. Задача 1. Игорь решил сделать домашнее задание
Слайд 1Применение признаков делимости чисел при решении заданий ЕГЭ
Работу выполнила Николаева Ольга
МБОУ «ВВСОШ №1 им. Исидора Барахова»
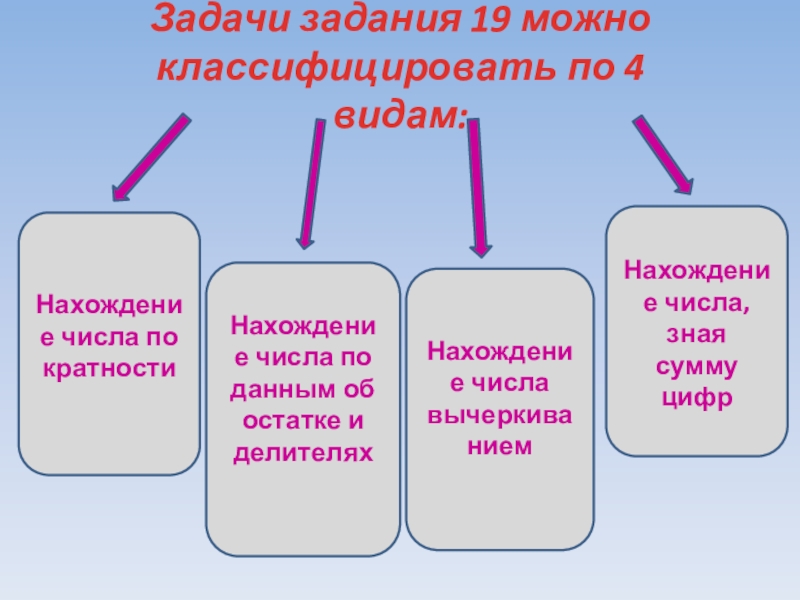
Слайд 4Задачи задания 19 можно классифицировать по 4 видам:
Нахождение числа по данным
Нахождение числа вычеркива нием
Нахождение числа, зная сумму цифр
Нахождение числа по кратности
Слайд 5Задача 1: Найдите четырехзначное число, кратное 18, произведение цифр которого равно
Примеры задач на нахождение числа по кратности
Слайд 6Решение. abcd :18 → d четное, но d≠0, т.к. a∙b∙c∙d=24. (a+b+c+d ):
Задача 1: Найдите четырехзначное число, кратное 18, произведение цифр которого равно 24. В ответе укажите какое-нибудь одно такое число.
Слайд 7Примеры задач на нахождение числа по данным об остатке и делителях
1. Найдите наименьшее трехзначное натуральное число, которое при делении на 6 и на 11 дает равные ненулевые остатки и у которого средняя цифра является средним арифметическим двух крайних цифр.
2. Найдите наименьшее трехзначное натуральное число, которое при делении на 3, на 5 и на 7 дает в остатке 2 и в записи которого есть только две различные цифры.
3. Найдите наибольшее трехзначное натуральное число, которое при делении на 8 и на 5 дает равные ненулевые остатки и средняя цифра которого является средним арифметическим крайних цифр.
4. Приведите пример трёхзначного натурального числа, которое при делении на 4 и на 15 даёт равные ненулевые остатки и первая справа цифра которого является средним арифметическим двух других цифр. В ответе укажите ровно одно такое число.
Слайд 8Задача 1. Найдите наименьшее трехзначное натуральное число, которое при делении на
Решение. abc → 6n+r=11m+r, abc˳→: 2 → c˳ - четное,
b = (a + c) / 2. 3 → ( a+b+c˳):3,
11 → b=а+c˳ .
Число abc – наименьшее, тогда а=1; c˳=0 → b=а+c˳=1+0=1 → 1+1+0=2 - не подходит. При c˳=2 → b=а+c˳= 1+2=3→ 1+3+2=6 подойдет. 132 нацело делится на 2, 3, 11. Проводим подбор. Пусть остаток r=1, тогда 132+1=133. Проверим условие задачи 3=(1+3)/2 – не подходит. Проверяем r=2→ 134 не подойдет. Пусть r=3, тогда 132+3=135. Проверим условие задачи 3=(1+5)/2. Подходит. Ответ: 135
Слайд 9 Примеры задач на нахождение числа вычеркиванием
1. Вычеркните в числе 85417627
2. Вычеркните в числе 35242345 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите ровно одно получившееся число.
3. Вычеркните в числе 84164718 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите ровно одно получившееся число.
4. Вычеркните в числе 87451257 три цифры так, чтобы получившееся число делилось на 15. В ответе укажите ровно одно получившееся число.
Слайд 10Задача1. Вычеркните в числе 85417627 три цифры так, чтобы получившееся число
Решение. 85417627 :18 2→ е-четное, вычеркнем 7;
9→ (a+b+c+d+е ): 9 → сумма цифр = (9 или 18 или 27)˂33, т.к. 8 + 5 + 4 + 1 + 7 + 6 + 2 = 33. 1) 33-27=6→ вычеркиваем цифры 4и2→85176 и вычеркиваем 5и1→ 84762. 2) 33-18=15→ вычеркиваем цифры8 и 7 →54162. 3) 33-9=24 не получается. Ответ: 85176 или 84762 или 54162.
Слайд 11
Примеры задач на нахождение числа,
зная сумму цифр
1. Сумма цифр трёхзначного
2. Найдите трехзначное число А, обладающее всеми следующими свойствами:
Сумма цифр числа А делится на 4;
Сумма цифр числа (А + 2) делится на 4;
Число А больше 200 и меньше 400.
В ответе укажите какое-нибудь одно такое число.
3. Найдите трехзначное число А, обладающее всеми следующими свойствами:
Сумма цифр числа А делится на 8;
Сумма цифр числа (А + 2) делится на 8;
Число А больше 1500 и меньше 1700.
В ответе укажите какое-нибудь одно такое число.
Слайд 12Задача 1. Сумма цифр трёхзначного натурального числа А делится на 12.
Решение. Заметим, что сумма цифр числа A + 6 должна отличаться от суммы цифр числа A на 12, 24, ... .
аbc если c < 4, то a + b + c + 6 не подходит;
если c ≥ 4 и b < 9, то a + b + 1 + c - 4 = a + b + c – 3 не подойдет; если c ≥ 4, b = 9, a < 9, то 9-(-3)=12 подойдет.
а+b+c = 24→ b =9 → а +c=24-9=15 → c = 4 и a = 11 и с=5 и а=10 - не подходят. c = 6 и a = 9 → 996; c = 7 и a = 8 → 897; c = 8 и a = 7 → 798; c = 9 и a = 6 → 699. Минимальным является 699. Проверим, 6 + 9 + 9 = 24, 24 / 12 = 2 → 699 + 6 = 705, 7 + 0 + 5 = 12, 12 / 12 = 1 Ответ: 699
Слайд 13Задача 1. Игорь решил сделать домашнее задание по математике с Колей
Примеры задач из задания 20, при решении которых применяется делимость чисел
Слайд 14Задача 1. Игорь решил сделать домашнее задание по математике с Колей
Решение. Трехзначное число количество квартир авс ˃ 206.
авс :5 → с=0 или 5;
:9 → (а+в+с):9. Если а=2 и с=0, то в=7(270делится на 9). Число 270:5 =54- количество квартир в подъезде, 54:9=6-количество квартир на каждом этаже, тогда 206-4·54=206-216<0. Не подходит.
Если с=5, то 225:5=45 – количество квартир в каждом подъезде. 45:9=5 – количество квартир на каждом этаже. 206 - 4∙45=206-180=26 → 26:5=5(остаток 1). Коля живет в 6 этаже. Ответ: 6