- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Применение показательной и логарифмической функций в природе и технике
Содержание
- 1. Презентация по математике на тему Применение показательной и логарифмической функций в природе и технике
- 2. Слайд 2
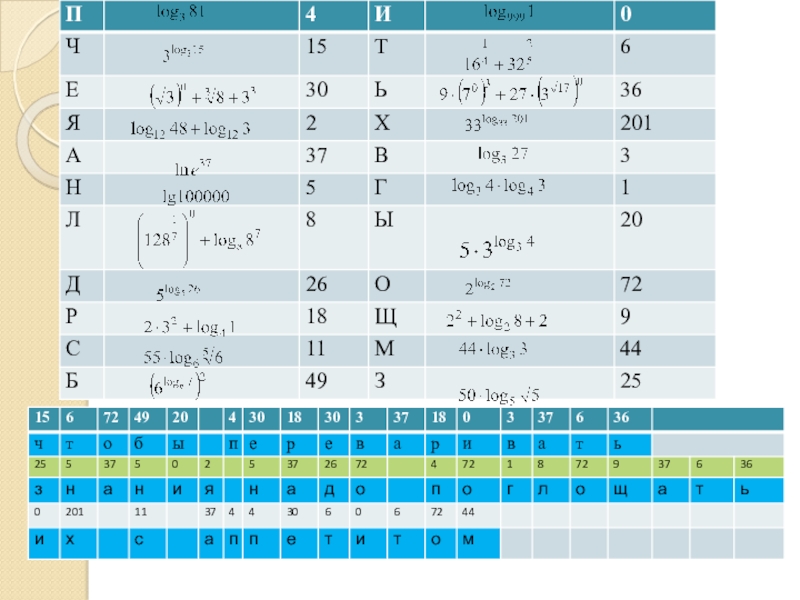
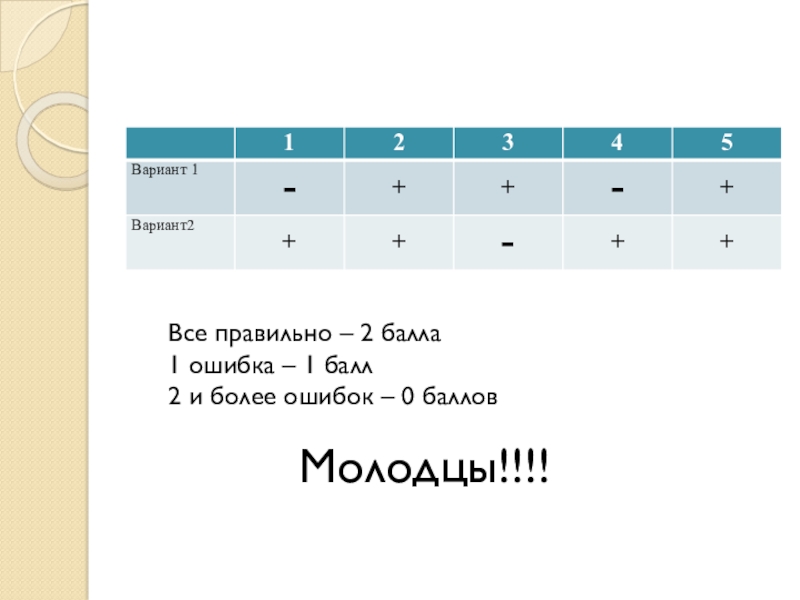
- 3. Все правильно – 2 балла1 ошибка – 1 балл2 и более ошибок – 0 балловМолодцы!!!!
- 4. Задача №1. Некоторая сумма денег в 12
- 5. Слайд 5
- 6. Руководствуясь формулой сложных процентов, имеем уравнение относительно nЛогарифмируя это уравнение по основанию 10, получимОткуда,
- 7. Слайд 7
- 8. Логарифмы в географии Для планирования развития
- 9. Логарифмы в физикеРадиоактивный распад. Изменение массы радиоактивного вещества
- 10. По вертикальной оси отложим блеск звезд
- 11. Пусть в начальный момент времени имелось q
Слайд 1
Применение показательной и логарифмической функций в природе и технике.
«Гениальное изобретение логарифмов,
Французский философ и математик Жан Кондорсе
Слайд 4Задача №1.
Некоторая сумма денег в 12 000 руб. подвержена приросту
Задача №2.
В начальный момент времени было 8 бактерий, через 2 ч после помещения бактерий в питательную среду их число возросло до 100. Через сколько времени с момента помещения в питательную среду следует ожидать колонию в 500 бактерий.
Задача №3
Определите возраст остатков мамонта, найденных в вечной мерзлоте на Таймыре, если относительное содержание изотопа C14 в них составляет 26% от его количества в живом организме.
Задача №4
Давление в городе Курск на 21 ноября 2017 года равно 738 мм рт. ст. Вычислите, на какой высоте находится наш город.
Задача №5
В начальный момент времени масса изотопа 40 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.?
Слайд 5 Пусть банк начисляет p% годовых, внесенная сумма равна А руб., а
Слайд 6
Руководствуясь формулой сложных процентов, имеем уравнение
относительно n
Логарифмируя это уравнение по
Откуда,
Слайд 7 Логарифмы в химии и биофизике. Для чего же нужны логарифмы в
Слайд 8Логарифмы в географии Для планирования развития городов, других населенных пунктов, строительства жилья,
Используются логарифмы и в расчётах, связанных с изменением атмосферного давления при изменении высоты над уровнем моря.
Если давление у поверхности Земли р0=рн=101.325кПа и температура на любой высоте равна 00 С то
Тогда
где высота h выражена в километрах. Если давление р в мм ртутного столба, то
Формула (1) называется барометрической формулой высоты. При точных вычислениях атмосферного давления следует учитывать понижение температуры воздуха по мере увеличения высоты.
Слайд 9Логарифмы в физике
Радиоактивный распад. Изменение массы радиоактивного вещества происходит по формуле ,
где m0 – где масса вещества в начальный период времени t=0, m – масса вещества в момент времени t, .T - период полураспада. Это означает, что через время Т после начального момента времени, масса радиоактивного вещества уменьшается вдвое.
Вредное влияние промышленных шумов на здоровье рабочих и на производительность труда побудило выработать приемы точной числовой оценки громкости шума. Единицей громкости служит “бел”, но практически используются единицы громкости, равные его десятой доле, - так называемые “децибелы”. Последовательность степени громкости 1 бел, 2 бела и т. д. составляют арифметическую прогрессию. Физические же величины, характеризующие шумы (энергия, интенсивность звука и др.), составляют геометрическую прогрессию со знаменателем 10. Громкость, выраженная в белах, равна десятичному логарифму соответствующей физической величины
. Рассмотрим несколько примеров: тихий шелест листьев оценивается в 1 бел, громкая разговорная речь – в 6,5 бела, рычанье льва – в 8,7 бел, шум Ниагарского водопада – 9 бел. Отсюда следует, что по силе звука разговорная речь превышает шелест листьев.
Слайд 10 По вертикальной оси отложим блеск звезд
Звезды, шум и логарифмы
Слайд 11Пусть в начальный момент времени имелось q единиц некоторого компонента. В
Процессы, у которых происходит быстрый рост или быстрое затухание, описываются показательной функцией вида
В нашем случае будем считать, что начальный момент времени соответствует нулю, тогда
и значит, c0 =q, т.е. функция, описывающая этот процесс, имеет вид
В следующий момент времени t у нас произошли изменения, описываемые уравнением
, т.е. p=at,
тогда lg p=lg at, lg p=tlga,
Таким образом, по данным условия мы получаем функцию
мы ищем x, при котором y=B, т.е. надо решить уравнение
Выполним логарифмирование уравнения по основанию 10, получим