Нестерук
Анна Романовна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Применение разложения квадратного трёхчлена на множители в решении задач функциональной линии (9 класс)
Содержание
- 1. Презентация по математике на тему Применение разложения квадратного трёхчлена на множители в решении задач функциональной линии (9 класс)
- 2. ПовторениеВспомните теорему о разложении квадратного трехчлена на
- 3. Когда квадратный трехчлен нельзя разложить на множители,
- 4. Решение простейших задачНули квадратичной функции вида
- 5. Решение задач в табличном процессоре ExcelПостройте
- 6. Данная книга рассчитана на построениефункций вида:Решение задач в табличном процессоре Excel
- 7. В таблицу «Данные» введите известные вамкоэффициенты. Решение задач в табличном процессоре Excel
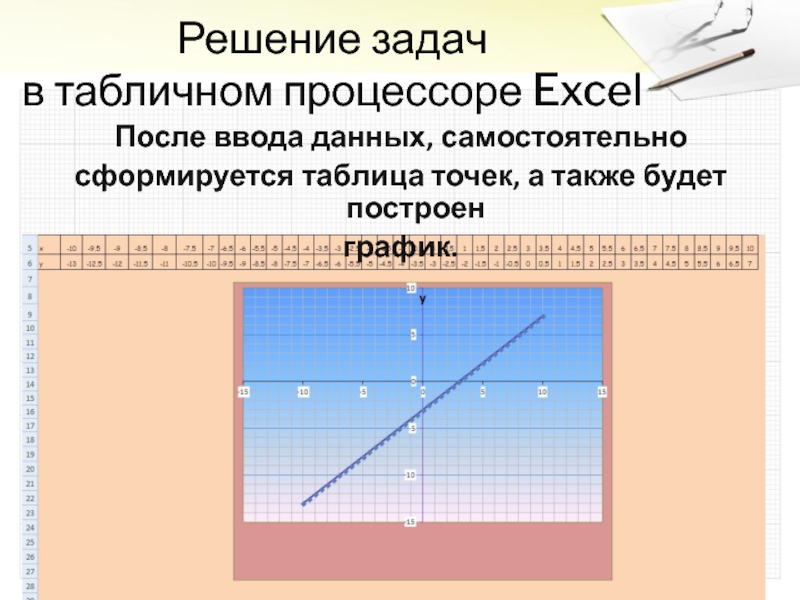
- 8. Решение задач в табличном процессоре ExcelПосле ввода данных, самостоятельносформируется таблица точек, а также будет построенграфик.
- 9. Построив график, нужно учитывать, что нами былПостроен
- 10. Задача 1 Постройте график функции и определите,
- 11. Шаг 1. Нахождение ОДЗЗнаменатель функции
- 12. Преобразуем функцию Шаг 2. Преобразование функцииЗнаменатель разложим на множители по формуле
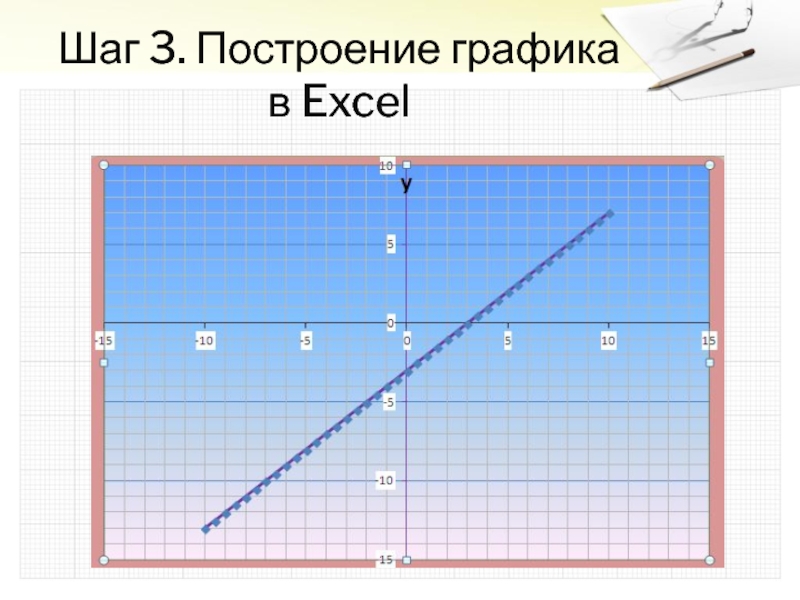
- 13. Шаг 3. Построение графика в Excel
- 14. График – прямая
- 15. Решение задач самостоятельноПостройте график функции и определите,
- 16. Домашнее заданиеПостройте график функции и определите, при
- 17. Спасибо за урок!
ПовторениеВспомните теорему о разложении квадратного трехчлена на множители.Какое значение переменной называется корнем квадратного трехчлена? Если и - корни квадратного трёхчлена
Слайд 1Применение разложения квадратного трёхчлена на множители в решении задач функциональной линии
Учитель:
Слайд 2Повторение
Вспомните теорему о разложении квадратного трехчлена на множители.
Какое значение переменной называется
корнем квадратного трехчлена?
Если и - корни квадратного трёхчлена , то
Значение переменной, при котором значение многочлена обращается в ноль.
Слайд 3Когда квадратный трехчлен нельзя разложить на множители, являющиеся многочленами первой степени?
Какие
ещё способы разложения на множители вы знаете?
Повторение
Если он не имеет корней
Вынесение за скобки общего множителя;
Способ группировки;
С помощью применения формул сокращённого умножения.
Слайд 4Решение простейших задач
Нули квадратичной функции вида
числа 3 и -5. Какой вид имеет данная функция?
Решение:
Функция имеет вид квадратного трёхчлена,
старший коэффициент которого равен 1.
Если 3 и -5 нули функции, то это корни
квадратного трёхчлена.
Перемножим скобки:
Подставим 3 и -5 в формулу разложения:
Значит, исходная функция имеет вид:
Слайд 5Решение задач
в табличном процессоре Excel
Постройте график функции
Шаг 1: Найдите ОДЗ
функции
Шаг 2: Сократите дробь
Шаг 3: Запустите на компьютерах документ «Построение графиков функций»
Слайд 7В таблицу «Данные» введите известные вам
коэффициенты.
Решение задач
в табличном процессоре
Excel
Слайд 8Решение задач
в табличном процессоре Excel
После ввода данных, самостоятельно
сформируется таблица точек,
а также будет построен
график.
график.
Слайд 9Построив график, нужно учитывать, что нами был
Построен график сокращённой функции
,
а следовательно не было учитано ОДЗ.
а следовательно не было учитано ОДЗ.
Решение задач
в табличном процессоре Excel
При решении задач
ПОМНИТЕ!
В зависимости от ОДЗ, на графике могут появиться
выколотые точки
Слайд 10Задача 1 Постройте график функции
и определите, при каких значениях
построенный график
не будет иметь общих
точек с прямой .
точек с прямой .
Решение задач
в табличном процессоре Excel
Слайд 11Шаг 1. Нахождение ОДЗ
Знаменатель функции
имеет вид квадратного трёхчлена.
Найдём его корни:
Найдём его корни:
Запишем ОДЗ:
Слайд 12Преобразуем функцию
Шаг 2. Преобразование функции
Знаменатель разложим на множители по формуле
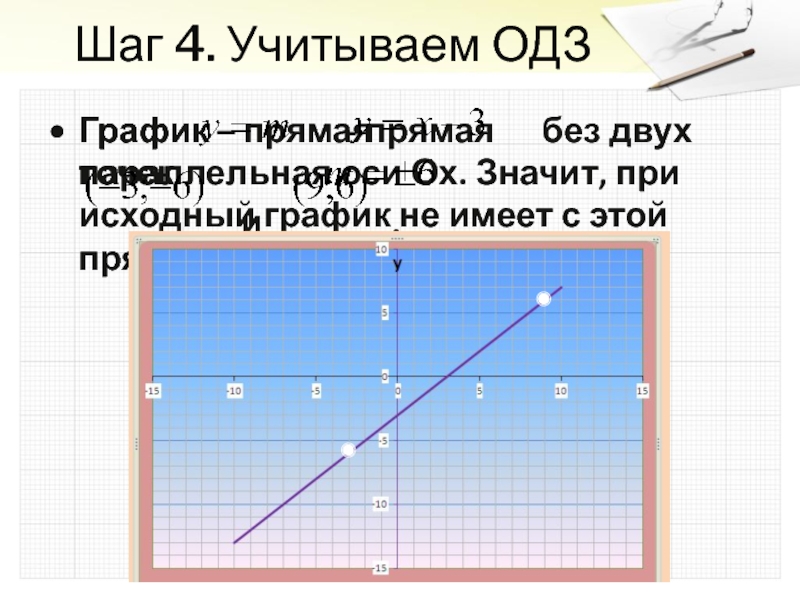
Слайд 14График – прямая
без двух точек
и .
и .
График - прямая параллельная оси Ох. Значит, при исходный график не имеет с этой прямой общих точек.
Шаг 4. Учитываем ОДЗ
Слайд 15Решение задач самостоятельно
Постройте график функции
и определите, при каких значениях
прямая
имеет с графиком ровно
одну общую точку.
одну общую точку.
Постройте график функции
и определите, при каких значениях
прямая имеет с графиком ровно
одну общую точку.
Слайд 16Домашнее задание
Постройте график функции
и определите, при каких значениях
прямые
, имеют с графиком ровно
одну общую точку.
одну общую точку.
