- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Последовательность Фибоначчи (9 класс)
Содержание
- 1. Презентация по математике на тему Последовательность Фибоначчи (9 класс)
- 2. Об авторе последовательности – Леонардо Пизанском (Фибоначчи)
- 3. Именно в «Книге абака» впервые приводится
- 4. Последовательность Фибоначчи: {1, 1, 2, 3,
- 5. Последовательность Фибоначчи и золотое сечение Пятиконечная звезда
- 6. Числа ф и φ Рассмотрим отношение AD:AC
- 7. Связь числа ф с последовательностью Фибоначчи Число
- 8. Парфенон в Афинах
- 9. Золотой прямоугольник
- 10. Разумеется, бывает и «золотой треугольник». На
- 11. Леонардо да Винчи использовал «золотой треугольник» в композиции своей знаменитой «Джоконды»
- 12. Вычисление и печать n первых членов последовательности
- 13. Program F1;uses crt;type tv=array[1.. 20] of integer;var
- 14. Второй способ вычисления и печати n первых
- 15. Свойства чисел Фибоначчи.Числа Фибоначчи это последовательность из
- 16. Последовательность Фибоначчи — это не просто игра
- 17. 1)Н.М.Воробьёв, Числа Фибоначчи, Москва, Наука, 1992. 2)А.И.Маркушевич,
Слайд 1Выполнили:
Хорсов Евгений,
Серёгин Александр,
Майхов Павел.
Руководитель:
Славинская Галина Николаевна.
Последовательность Фибоначчи.
Слайд 2Об авторе последовательности – Леонардо Пизанском (Фибоначчи)
Среди современников ему не
И в последующие три столетия нельзя назвать ни одного учёного такого масштаба.
Леонардо родился в большом итальянском торговом городе Пизе в семье нотариуса.
Леонардо Пизанский(1180-1240) оказал решающие влияние на развитие алгебры и теории чисел.
Знаменита его «Книга абака»(1202 год) –
настоящая энциклопедия математических
знаний его эпохи. В этой книге рассматриваются
вопросы алгебры, геометрии и теории чисел.
Слайд 3 Именно в «Книге абака» впервые приводится решение известной задачи о
Ответ даётся суммой ряда: 1+1+2+3+5+...+144.
Каждый член этого ряда, начиная с третьего, является суммой двух предыдущих. Члены ряда называются числами Фибоначчи.
Слайд 4Последовательность Фибоначчи:
{1, 1, 2, 3, 5, 8, 13…}
Последовательность задаётся
a1=1
a2=1
an=an-1+an-2 (n≥3)
Формула вычисления an:
Заметим, что | |<1 и уже при n=30:
| |< 1 .
С ростом n an ≈ фn , ф = 1+√5 .
1000000
√5
2
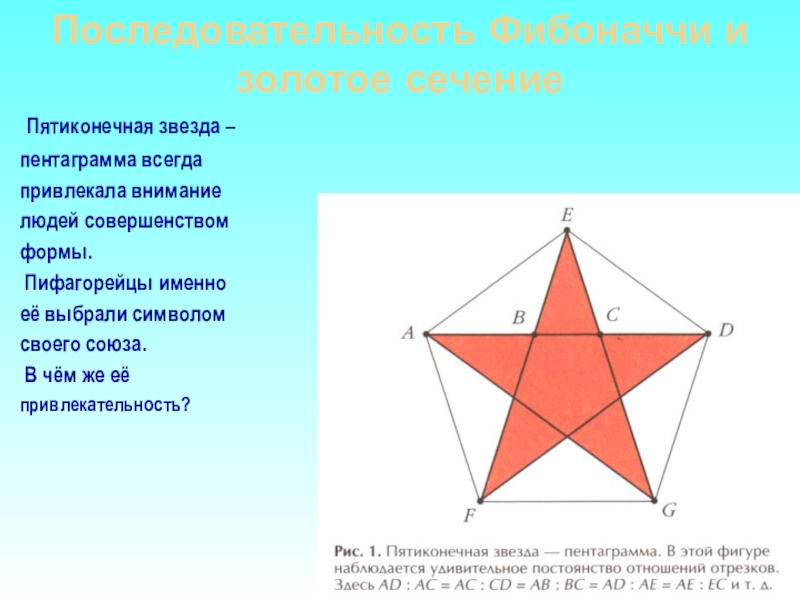
Слайд 5Последовательность Фибоначчи и золотое сечение
Пятиконечная звезда –
пентаграмма всегда
привлекала
людей совершенством
формы.
Пифагорейцы именно
её выбрали символом
своего союза.
В чём же её
привлекательность?
Слайд 6Числа ф и φ
Рассмотрим отношение AD:AC = AC:CD .
a:b = b:(a-b) .
Разделим обе части равенства на b² и обозначим a = ф.
Получим уравнение ф²= ф+1, имеющие единственный положительный корень:
ф = 1+√5 = 1,618034…
Часто рассматривают отношение φ = 1 = √5-1 = 0,618034…
Такое обозначение принято в честь древнегреческого скульптора Фидия, жившего в V веке до н.э.
Фидий руководил строительством храма Парфенон в Афинах. В пропорциях этого храма многократно присутствует число φ .
b
2
2
ф
Слайд 7Связь числа ф с последовательностью Фибоначчи
Число ф тесно связано с
где an= 1[фn-φn], Интересно отметить, что
фn = 1 (an√5+bn), где
an – n-е число Фибоначчи, а bn – n-й член последовательности 1, 3, 4, 7, 11, 18, 29… , образующейся по тому же принципу, что и последовательность Фибоначчи.
√5
2
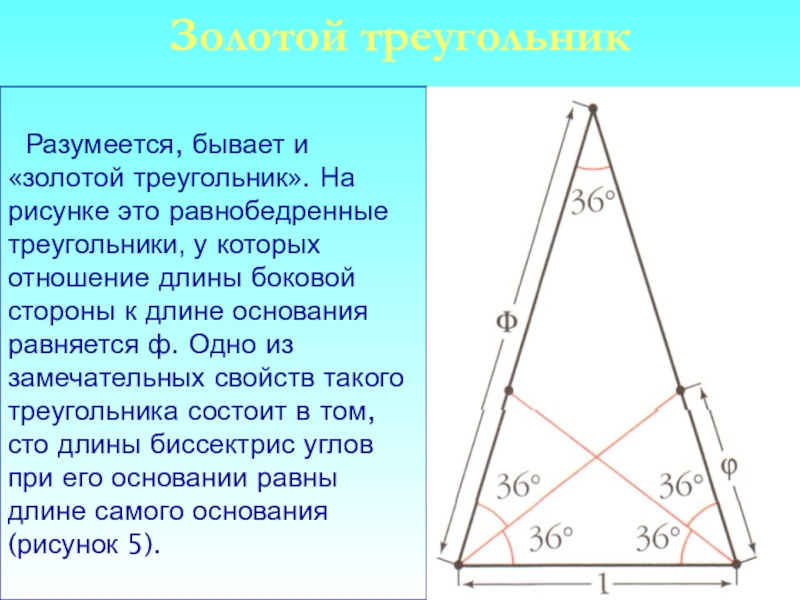
Слайд 10 Разумеется, бывает и «золотой треугольник». На рисунке это равнобедренные треугольники,
Золотой треугольник
Слайд 11Леонардо да Винчи использовал «золотой треугольник» в композиции своей знаменитой «Джоконды»
Слайд 12Вычисление и печать n первых членов последовательности Фибоначчи с использованием компьютера
По
a1=a2=1;
an=an-1+an-2.
(n ≥3)
начало
a[1], a[2],
n
i≤ n
i:=3
a[1]: a[ i-1]+a[ i-2]
i: i+1
{a[i]}
конец
да
нет
Блок – схема
Слайд 13Program F1;
uses crt;
type tv=array[1.. 20] of integer;
var a: tv; n,i,j,k: integer;
begin
clrscr;
writeln
readln (n);
a[1]:=1;
a[2]:=1;
for i:=3 to n do
begin
j:=i-2;
k:=i-1;
a[i]:=a[j]+a[k];
end;
for i:=1 to n do
begin
write(a[i]:6);
writeln;
end;
readkey;
end.
Нахождение первых
20 чисел Фибоначчи при помощи языка Турбо Паскаль
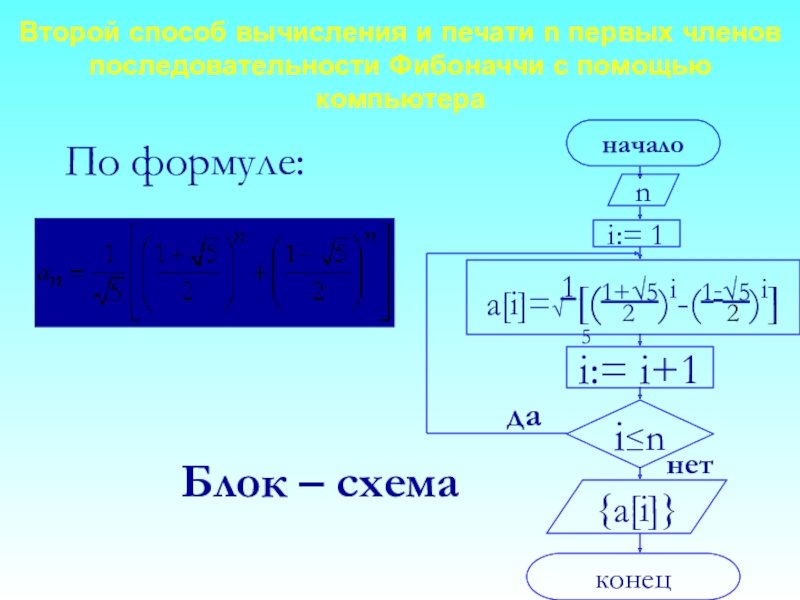
Слайд 14Второй способ вычисления и печати n первых членов последовательности Фибоначчи с
По формуле:
начало
n
i:= i+1
a[i]= 1[(1+√5)i-(1-√5)i]
i:= 1
√5
2
2
i≤n
{a[i]}
конец
нет
да
Блок – схема
Слайд 15Свойства чисел Фибоначчи.
Числа Фибоначчи это последовательность из чисел 1, 1, 2,
1. Каждое число ряда представляет собой сумму двух предыдущих чисел.
2. Отношение любого числа ряда к предыдущему стремится к 1,618.
3. Отношение любого числа ряда к последующему стремится к 0,618.
4. Отношение любого числа ряда к предыдущему через одно стремится к 2,618.
5. Отношение любого числа ряда к последующему через одно стремится к 0,382.
Слайд 16Последовательность Фибоначчи — это не просто игра с числами, а самое
Последовательность Фибоначчи остаётся математической каббалой по сей день, и каждое новое открытие бросает новый отблеск на магию этих цифр.
Слайд 171)Н.М.Воробьёв, Числа Фибоначчи, Москва, Наука, 1992.
2)А.И.Маркушевич, Возврватные последовательности, Москва, Наука,
3)Энциклопедия для детей. Математика Москва, «Акванта +»,1998г.
4) http://pascalstudy.narod.ru/
5) http://www.math24.ru/
Литература





![Презентация по математике на тему Последовательность Фибоначчи (9 класс) Связь числа ф с последовательностью Фибоначчи Число ф тесно связано с Связь числа ф с последовательностью Фибоначчи Число ф тесно связано с последовательностью Фибоначчи; где an= 1[фn-φn], Интересно](/img/thumbs/df6b2f878b518b17b64175cf57748aa7-800x.jpg)



![Презентация по математике на тему Последовательность Фибоначчи (9 класс) Вычисление и печать n первых членов последовательности Фибоначчи с использованием компьютераПо Вычисление и печать n первых членов последовательности Фибоначчи с использованием компьютераПо рекуррентной формуле:a1=a2=1;an=an-1+an-2. (n ≥3)началоa[1], a[2],ni≤ ni:=3](/img/thumbs/49a87f4b3b7fa5d93896a627eca53812-800x.jpg)
![Презентация по математике на тему Последовательность Фибоначчи (9 класс) Program F1;uses crt;type tv=array[1.. 20] of integer;var a: tv; n,i,j,k: integer;beginclrscr;writeln Program F1;uses crt;type tv=array[1.. 20] of integer;var a: tv; n,i,j,k: integer;beginclrscr;writeln ('n=');readln (n);a[1]:=1;a[2]:=1;for i:=3 to n dobegin](/img/thumbs/a1ea8836f11b34dc32cae00490e9f9f5-800x.jpg)