- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Полярные координаты
Содержание
- 1. Презентация по математике на тему Полярные координаты
- 2. Гипотеза: я считаю, что полярная система координат
- 3. Греческий астроном Гиппарх применил полярные координаты для
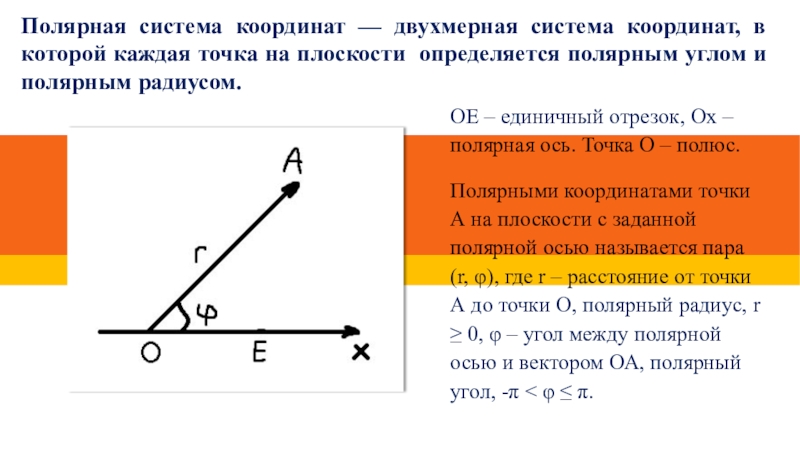
- 4. Полярная система координат — двухмерная система координат,
- 5. Полярная система координат связана с декартовой, где
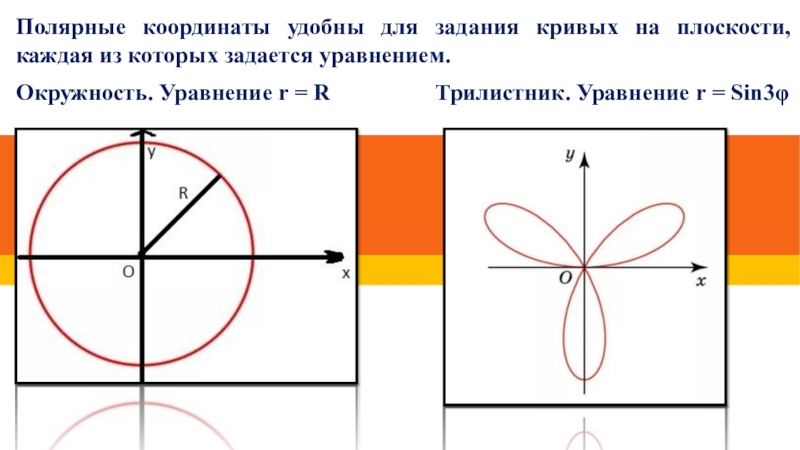
- 6. Полярные координаты удобны для задания кривых на
- 7. Спираль Архимеда – кривая, задаваемая уравнением r
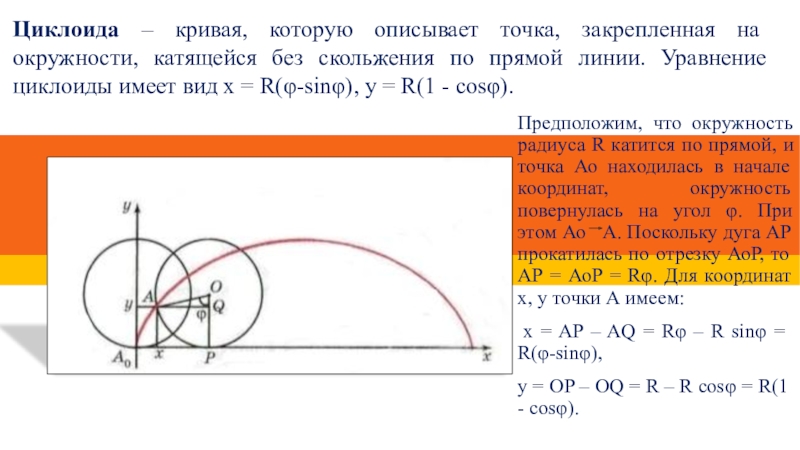
- 8. Циклоида – кривая, которую описывает точка, закрепленная
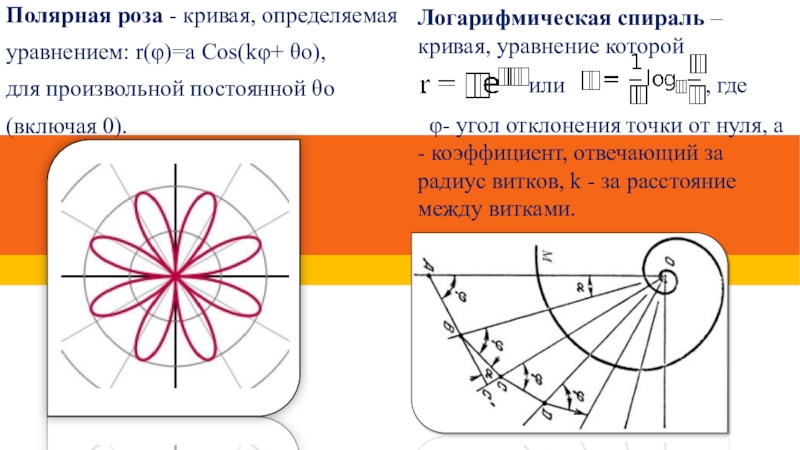
- 9. Логарифмическая спираль – кривая, уравнение которой
- 10. Задания. Построить кривую, заданную уравнением r =
- 11. Применение полярных систем координатСпираль Архимеда
- 12. Логарифмическая спираль
- 13. В техникеЦиклоидаЛогарифмическая спираль
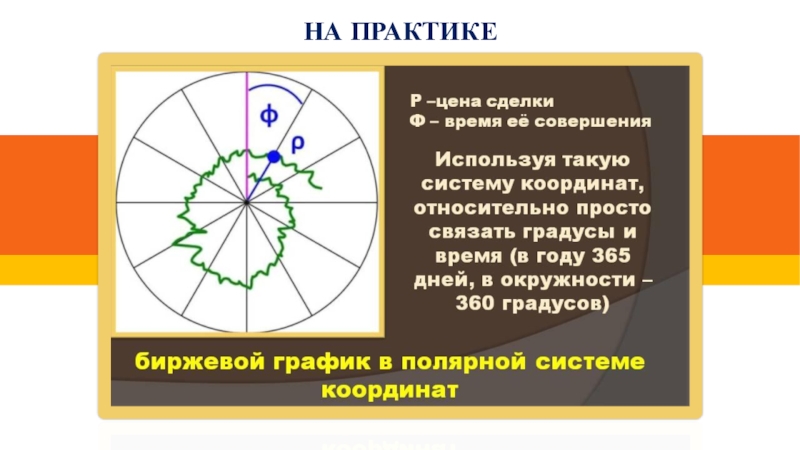
- 14. На практике
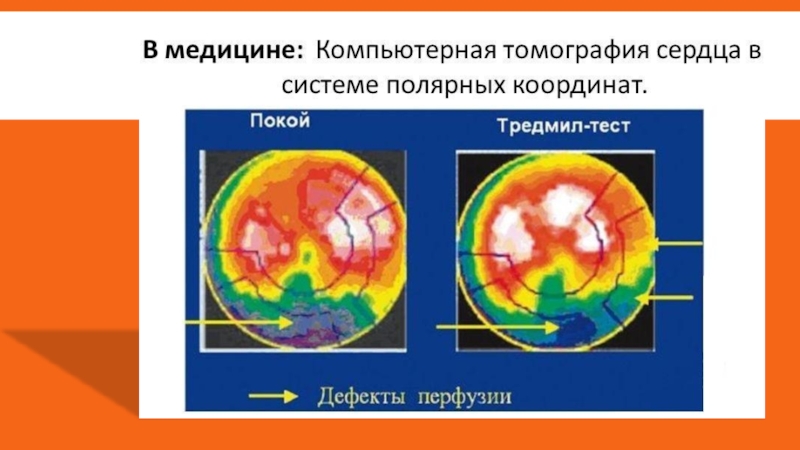
- 15. Слайд 15
- 16. Слайд 16
- 17. Радиолокационная станция
- 18. ЗаключениеВыполнив данную исследовательскую работу, я сделала следующий
- 19. Спасибо за внимание!
Слайд 1Исследовательская работа
Теория и практическое применение полярной системы координат
Выполнила: ученица 10 Б
Лобанова Софья
Научный руководитель: Мощенко О.В.
учитель математики МБОУ СОШ № 11
Слайд 2Гипотеза: я считаю, что полярная система координат может найти широкое применение
Слайд 3Греческий астроном Гиппарх применил полярные координаты для определения положения небесных тел.
Гиппарх (190 г. до н. э. – 120 г.)
Грегорио Фонтана
Леонард Эйлер
Слайд 4Полярная система координат — двухмерная система координат, в которой каждая точка
ОЕ – единичный отрезок, Ох –полярная ось. Точка О – полюс.
Полярными координатами точки А на плоскости с заданной полярной осью называется пара (r, φ), где r – расстояние от точки А до точки О, полярный радиус, r ≥ 0, φ – угол между полярной осью и вектором ОА, полярный угол, -π < φ ≤ π.
Слайд 5Полярная система координат связана с декартовой, где за полюс считается начало
Ох – полярная ось,
ОА – полярный радиус,
точка О – полюс, начало координат,
φ – полярный угол.
Слайд 6Полярные координаты удобны для задания кривых на плоскости, каждая из которых
Окружность. Уравнение r = R Трилистник. Уравнение r = Sin3φ
Слайд 7Спираль Архимеда – кривая, задаваемая уравнением r = aφ, где a
Геометрическое свойство спирали Архимеда – постоянство расстояний между соседними витками, каждое из них равно 2πa.
Действительно, если на 2π, т. е. точка делает один оборот против часовой стрелки, то радиус увеличивается на 2πa, что и составляет расстояние между соседними витками.
Слайд 8Циклоида – кривая, которую описывает точка, закрепленная на окружности, катящейся без
Предположим, что окружность радиуса R катится по прямой, и точка Ао находилась в начале координат, окружность повернулась на угол φ. При этом Ао А. Поскольку дуга AP прокатилась по отрезку АоР, то АР = АоР = Rφ. Для координат x, y точки А имеем:
x = AP – AQ = Rφ – R sinφ = R(φ-sinφ),
y = OP – OQ = R – R cosφ = R(1 - cosφ).
Слайд 9Логарифмическая спираль – кривая, уравнение которой
φ- угол отклонения точки от нуля, а - коэффициент, отвечающий за радиус витков, k - за расстояние между витками.
Полярная роза - кривая, определяемая
уравнением: r(φ)=a Cos(kφ+ θo),
для произвольной постоянной θо
(включая 0).
Слайд 10Задания. Построить кривую, заданную уравнением r = Sinф.
Для этого нужно построить
Соединим все точки и получим:
Слайд 18Заключение
Выполнив данную исследовательскую работу, я сделала следующий вывод - полярные системы
Следует также отметить, что они, являясь относительно легкими в построении, могли бы быть включены в общеобразовательную программу школы, ведь их изучение позволило бы заинтересовать некоторых студентов в том, чтобы связать в дальнейшем свою жизнь и карьеру с техникой, прикладными науками.