- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему погрешности для 1 курса
Содержание
- 1. Презентация по математике на тему погрешности для 1 курса
- 2. Цели урока:Изучить понятия «абсолютная погрешность», «относительная погрешность»Научиться вычислять погрешности
- 3. вспомнимЧто называется модулем числа?
- 4. Слайд 4
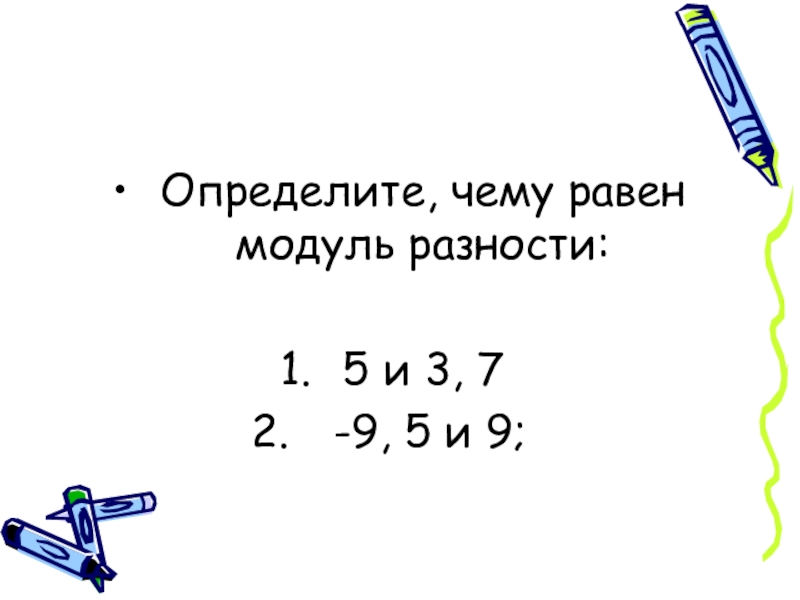
- 5. Определите, чему равен модуль разности: 5 и 3, 7 -9, 5 и 9;
- 6. Вспомним правило округления чисел
- 7. Правило округления. При округлении десятичной дроби до
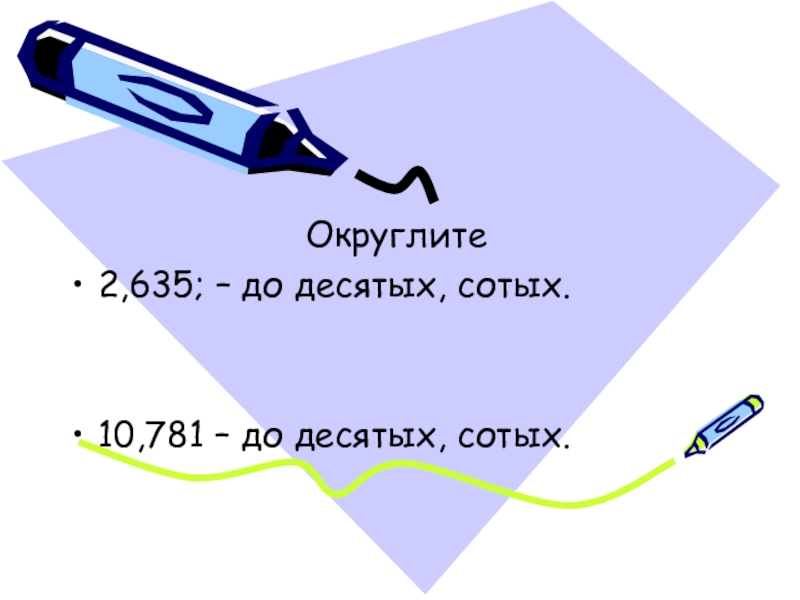
- 8. Округлите 2,635; – до десятых, сотых.10,781 – до десятых, сотых.
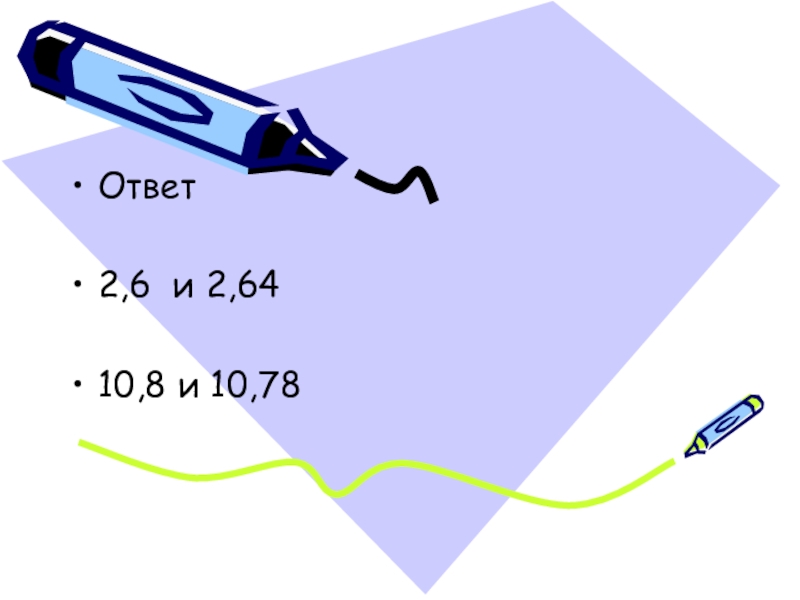
- 9. Ответ2,6 и 2,64 10,8 и 10,78
- 10. При округлении десятичных дробей до десятых, до
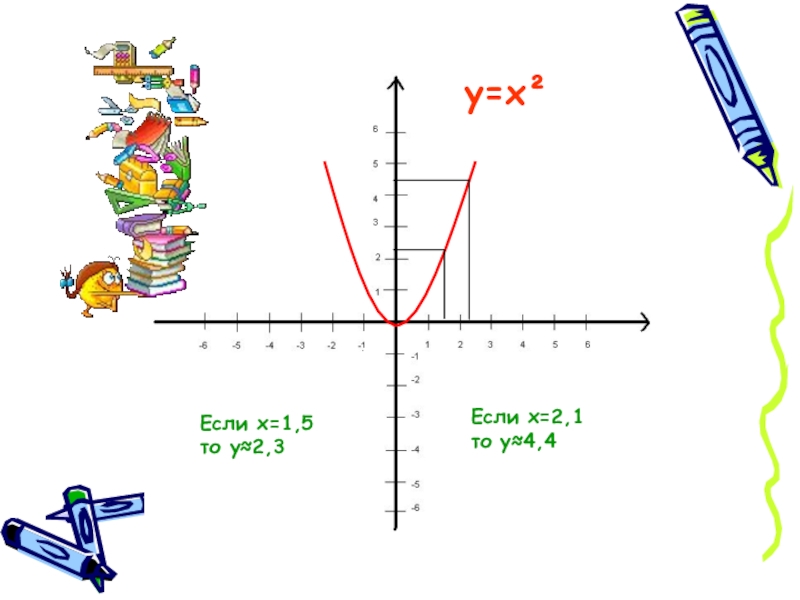
- 11. Если х=1,5 то у≈2,3Если х=2,1 то у≈4,4у=х²
- 12. По формуле у= х² найдем точные значения этой функции: Если х=1,5Если х=2,1то у=1,5² =2,25то у=2,1² =4,41
- 13. На сколько отличается приближенное значение от точного?2,3-2,25=0,054,41-4,4=0,01
- 14. Вывод: Чтобы узнать, на сколько приближенное значение
- 15. Абсолютной погрешностью приближенного значения называется модуль разности точного и приближенного значений.
- 16. А относительная погрешность оценивает качество измерения и выражается в процентах.
- 17. Если х ≈ α, где х
- 18. Рассмотрим примеры на вычисление погрешностей.
- 19. 1 21 2 3
- 20. Вычислим относительную погрешность этих приближений:0,128 : │1,6│=
- 21. Отчего зависит точность приближенного значения?
- 22. Она зависит от многих причин. Если приближенное
- 23. Слайд 23
- 24. Например, при изготовлении метровой линейки допускается
- 25. Всегда ли можно найти абсолютную и относительную погрешности?
- 26. Не всегда можно найти абсолютную погрешность, так
- 27. Если х≈а абсолютная погрешность этого приближенного значения
- 28. Слайд 28
- 29. Задача.Найдем относительную погрешность при измерении длины листа
- 30. Говорят, относительная погрешность в первом случае до
- 31. Найдите абсолютную и относительную погрешности, полученные в
- 32. На производстве при изготовлении деталей мы пользуемся
- 33. Относительная погрешность с точностью до 0,1% (т.е.
- 34. Из практических примеров можно сделать вывод, что
- 35. Задача При измерении длины стержня
- 36. ЗадачаНайдите абсолютную погрешность, полученную в результате округленияа)
- 37. какие из значений величин точные и какие
- 38. Найдите абсолютную погрешность 286≈2900,35≈0,46912≈690040,40,040,050,010,10,1122
- 39. Какова точность измерения? А)длина отрезка линейкой с
- 40. Приближенное значение величины равно
- 41. Домашнее задание1. При вычислении дробь
- 42. Подведение итогов урокаСформулируйте определение абсолютной погрешности.Если нельзя
- 43. Викторина Какие из измерений являются точными, а
- 44. Спасибо за внимание ☺
Слайд 2Цели урока:
Изучить понятия «абсолютная погрешность», «относительная погрешность»
Научиться вычислять погрешности
Слайд 7Правило округления.
При округлении десятичной дроби до какого-нибудь разряда все следующие за
Слайд 10При округлении десятичных дробей до десятых, до сотых, до тысячных и
Слайд 12По формуле у= х² найдем точные значения этой функции:
Если х=1,5
Если
то у=1,5² =2,25
то у=2,1² =4,41
Слайд 14Вывод: Чтобы узнать, на сколько приближенное значение отличается от точного, надо
Надо найти модуль разности точного и приближенного значения. Этот модуль разности называют абсолютной погрешностью.
Слайд 15Абсолютной погрешностью приближенного значения называется модуль разности точного и приближенного значений.
Слайд 17
Если х ≈ α, где х – точное значение, а
то абсолютная погрешность будет равна │х – α │,
а относительная:
│х – α │∕ │α│, умноженное на 100%
Слайд 19
1 2
1
2
3
4
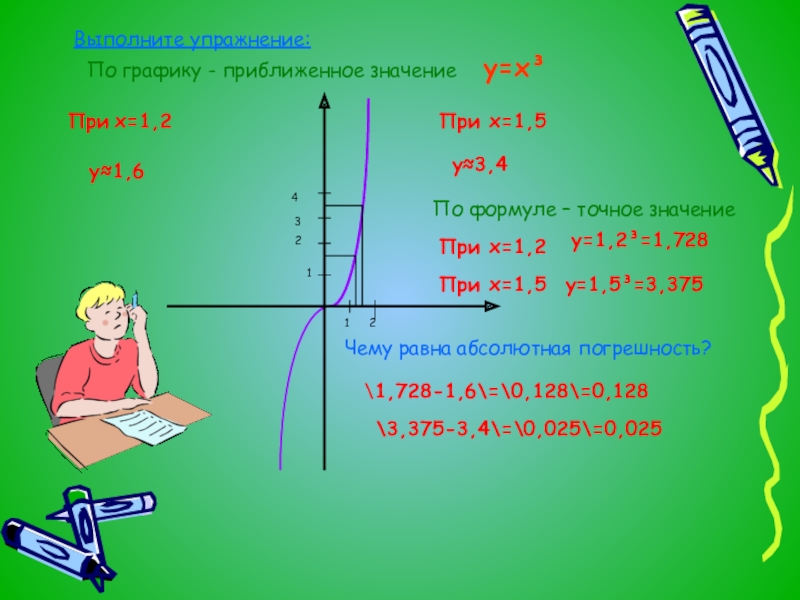
Выполните упражнение:
При х=1,2
При х=1,5
у≈3,4
По графику - приближенное значение
По формуле – точное значение
При х=1,2
у=1,2³=1,728
При х=1,5
у=1,5³=3,375
Чему равна абсолютная погрешность?
\1,728-1,6\=\0,128\=0,128
\3,375-3,4\=\0,025\=0,025
у=х³
Слайд 20Вычислим относительную погрешность этих приближений:
0,128 : │1,6│= 0, 128 : 1,6
0,08 = 8%
0,025 : │3,4│= 0, 025:3,4 = 0,007 = 0,7%
Слайд 22
Она зависит от многих причин. Если приближенное значение получено при измерении,
Слайд 24
Например, при изготовлении метровой линейки допускается погрешность 1мм. Само измерение
Округляя десятичную дробь до десятых точность будет до 0,1 ( ≤ 0,1); до сотых – точность до 0,01 ( ≤ 0,01).
Точнейшие в мире измерения производятся в лабораториях Института мер.
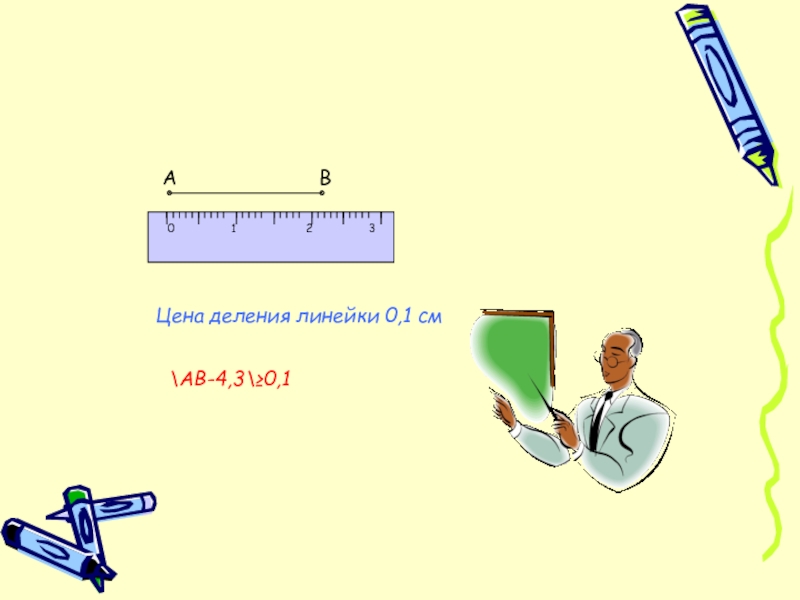
Слайд 26
Не всегда можно найти абсолютную погрешность, так как неизвестно
точное значение
В этом случае принято считать что абсолютная погрешность не превосходит цены деления шкалы прибора. Т.е. если например цена деления линейки 1мм = 0,1см, то абсолютная погрешность будет с точностью до 0,1 ( ≤ 0,1) и будет определена только оценка относительной погрешности (т.е. ≤ какому числу %).
Слайд 27Если х≈а абсолютная погрешность этого приближенного значения не превосходит некоторого числа
Слайд 29Задача.
Найдем относительную погрешность при измерении длины листа тетради линейками: одна –
ℓ1 = 20,4см ℓ2 = 20,2см
0,1 : 20,4 = 0,0049 = 0,49% 1 : 20,2 = 0,0495 = 4,95%
Слайд 30
Говорят, относительная погрешность в первом случае до 0,49%(т.е ≤ 0,49%), во
В первом случае точность измерения выше.
Мы говорим не о величине
относительной погрешности, а ее оценке.
Слайд 31
Найдите абсолютную и относительную погрешности, полученные в результате округления
а) до десятых
б) до десятков 124; 361; 720
Слайд 32
На производстве при изготовлении деталей мы пользуемся
штангенциркулем (для измерения глубины;
Абсолютная погрешность при измерении этим прибором составляет точность до 0,1мм. Найдем оценку относительной погрешности при измерении штангенциркулем:
d = 9,86см = 98,6мм
0,1 : │98,6│= 0,1 : 98,6 = 0,001 = 0,1%
Слайд 33
Относительная погрешность с точностью до 0,1% (т.е. ≤ 0,1%).
Слайд 34
Из практических примеров можно сделать вывод, что точных значений быть не
Но чтобы точнее выполнить измерение нужно взять измерительный прибор цена деления которого как можно меньше.
Слайд 35Задача
При измерении длины стержня пользовались линейкой, штангенциркулем, микрометром.
Слайд 36Задача
Найдите абсолютную погрешность, полученную в результате округления
а) до десятых 6,56; 0,475;
б) до десятков 124; 361; 720
Слайд 37какие из значений величин точные и какие приближенные?
Толщина книги 25
Температура воздуха 18*
В самолете 122 пассажира
Скорость звука в воздухе 322 м/с
Масса дыни 3,5 кг
Стоимость ручки 5 руб.
В тетради начерчен угол 50*
Рекорд соревнований в беге на 1500м равнялся 3мин 56с
Точные
Приближенные
Слайд 39Какова точность измерения?
А)длина отрезка линейкой с миллиметровой шкалой
Б)температура
В)масса на бытовых весах, цена деления шкалы которых равна 20г
Г)промежутков времени часами с секундной стрелкой
Д)градусной меры угла с помощью транспортира
Е)Объёма жидкости с помощью мензурки, цена деления которой 2мл
Слайд 40 Приближенное значение величины равно числу 17. Точность приближения
17,2
16,9
16,4
17,5
18
Да
Нет
Слайд 41Домашнее задание
1. При вычислении дробь заменили
2. Найдите с помощью графика функции y=x2 значение y при x =2,4.Вычислите погрешности полученного приближенного значения.
Слайд 42Подведение итогов урока
Сформулируйте определение абсолютной погрешности.
Если нельзя найти абсолютную погрешность, каким
Чему равна точность измерения?
Приведите примеры точности измерения некоторых приборов.
Для чего используется относительная погрешность?
Что такое относительная погрешность?
Слайд 43Викторина
Какие из измерений являются точными, а какие приближенными?
1. В классе
2. В рабочем поселке 1000 жителей
3. Железнодорожный рельс имеет длину 50 м
4. Рабочий получил в кассе 10 тысяч рублей
5. В самолете ЯК – 40 120 пассажирских мест
6. Расстояние между Москвой и Санкт – Петербургом 650 км
7. В килограмме пшеницы содержится 30000 зерен
8.Расстояние от Земли до Солнца 1,5 ∙ 108 км
9. Один из школьников на вопрос о том, сколько учащихся учится в школе, ответил: «1000», а другой ответил «950». Чей ответ точнее, если в школе учится 986 учащихся?
10. Буханка хлеба весит 1 кг и стоит 2500 р.
11. Тетрадь в 12 листов стоит 600 р. и имеет толщину 3 мм