Презентация, доклад по математике на тему Подготовка к ОГЭ (устная работа)

Содержание

1. Презентация по математике на тему Подготовка к ОГЭ (устная работа)
2. 1. Решите неравенство x²>4: А) (2; +∞);
3. 3. На рисунке изображены парабола и три
4. 4. Найдите шестой член последовательности, заданной рекуррентным

1. Решите неравенство x²>4: А) (2; +∞); Б) (- ∞; 2); В) (- ∞; -2) и (2; +∞); Г) (- ∞; -2] и [2; +∞); 2. Сколько корней имеет уравнение x³=4x²?А) 0; Б) 1;

Главная
Алгебра
Презентация по математике на тему Подготовка к ОГЭ (устная работа)

Слайд 1УСТНАЯ РАБОТА

Слайд 21. Решите неравенство x²>4:
А) (2; +∞);
Б) (- ∞;

2);
В) (- ∞; -2) и (2; +∞);
Г) (- ∞; -2] и [2; +∞);
2. Сколько корней имеет уравнение x³=4x²?
А) 0; Б) 1; В) 2; Г) 3.

1. Решите неравенство x²>4: А) (2; +∞); Б) (- ∞; 2); В) (- ∞; -2) и

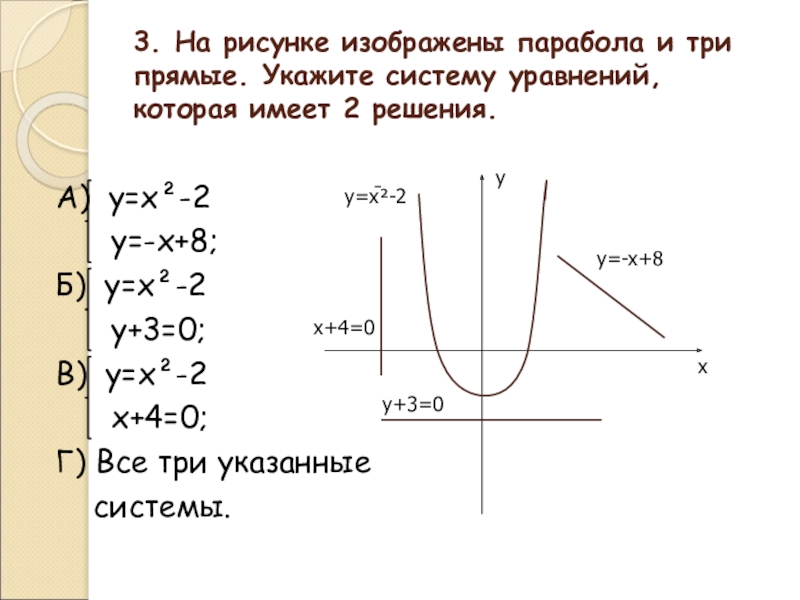
Слайд 33. На рисунке изображены парабола и три прямые. Укажите систему уравнений,

которая имеет 2 решения.

А) y=x²-2
y=-x+8;
Б) y=x²-2
y+3=0;
В) y=x²-2
x+4=0;
Г) Все три указанные
системы.

y=x²-2

x+4=0

y+3=0

y=-x+8

3. На рисунке изображены парабола и три прямые. Укажите систему уравнений, которая имеет 2 решения.А) y=x²-2

Слайд 44. Найдите шестой член последовательности, заданной рекуррентным способом b1=1, b2=1, bn+1

= bn-1 + bn (n>2).

А) 5; Б) 6; В) 7; Г) 8.

5. Поезд за первую минуту прошел 200м. За каждую следующую минуту поезд проходил на 100м больше, чем за предыдущую. Какое расстояние (в метрах) прошел поезд за n минут.
А) 100n+200; Б) 100n+100;
В) 200n+100; Г)200n+200.