- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Обратные тригонометрические функции (10 класс)
Содержание
- 1. Презентация по математике на тему Обратные тригонометрические функции (10 класс)
- 2. СодержаниеФункция y = arcsin x и ее
- 3. Функция y=arcsin x и ее свойстваЕсли |а|
- 4. Функция y=arcsin x и ее графикху01-1y=arcsin x y=x y=sin x π/2-π/2π
- 5. Функция y=arcsin x и ее свойстваD(y) =
- 6. Функция y=arccos x и ее свойстваЕсли |а|
- 7. Функция y=arcсоs x и ее графикху01-1πy=arcсоs x y=x y=соs x π/2π
- 8. Функция y=arccos x и ее свойстваD(y) =
- 9. Функция y=arctg x и ее свойстваarctg а
- 10. Функция y=arctg x и ее графикху01-1y=arctg x y=x y=tg x π/2-π/2ππ/4-π/4
- 11. Функция y=arctg x и ее свойстваD(y) =
- 12. Функция y=arcсtg x и ее свойстваarcсtg а
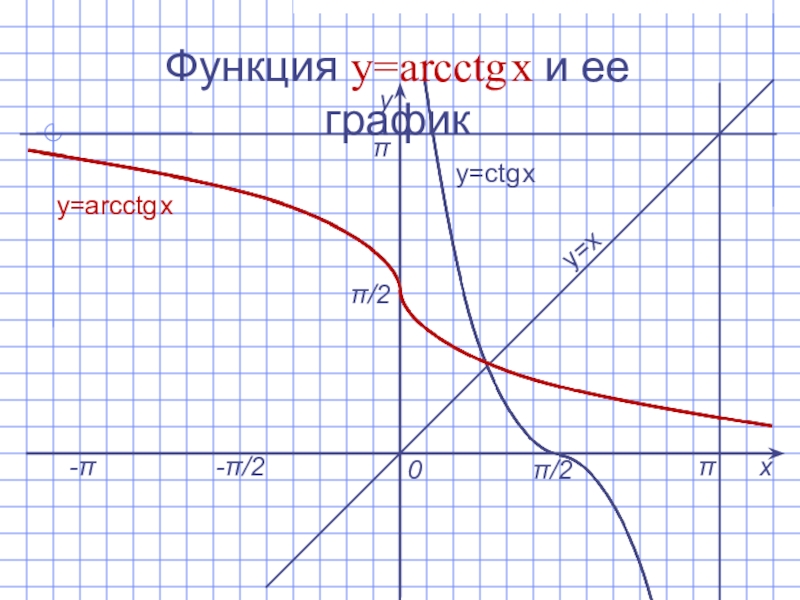
- 13. Функция y=arcсtg x и ее графикху0y=arcсtg x y=x y=сtg x -π/2π/2ππ/2π-π
- 14. Функция y=arcсtg x и ее свойстваD(y) =
СодержаниеФункция y = arcsin x и ее свойстваФункция y = arccos x и ее свойстваФункция y = arctg x и ее свойстваФункция y = arcctg x и ее свойства
Слайд 2Содержание
Функция y = arcsin x и ее свойства
Функция y = arccos
x и ее свойства
Функция y = arctg x и ее свойства
Функция y = arcctg x и ее свойства
Функция y = arctg x и ее свойства
Функция y = arcctg x и ее свойства
Слайд 3Функция y=arcsin x и ее свойства
Если |а| ≤ 1, то arcsin
а – это такое число из отрезка [-π/2;π/2], синус которого равен а.
Слайд 5Функция y=arcsin x и ее свойства
D(y) = [-1; 1].
E(y) = [-π/2;
π/2].
arcsin (-x) = - arcsin x – функция нечетная.
Функция возрастает на [-1; 1].
Функция непрерывна.
arcsin (-x) = - arcsin x – функция нечетная.
Функция возрастает на [-1; 1].
Функция непрерывна.
![Функция y=arcsin x и ее свойстваD(y) = [-1; 1].E(y) = [-π/2; π/2].arcsin (-x) = - arcsin x](/img/thumbs/c140d675456abe67a3f100d99a88eeb5-800x.jpg "Презентация по математике на тему Обратные тригонометрические функции (10 класс) Функция y=arcsin x и ее свойстваD(y) = [-1; 1].E(y) = [-π/2;")
Слайд 6Функция y=arccos x и ее свойства
Если |а| ≤ 1, то arccos
а – это такое число из отрезка [0; π], косинус которого равен а.
Слайд 8Функция y=arccos x и ее свойства
D(y) = [-1; 1].
E(y) = [0;
π].
Функция не является ни четной, ни нечетной.
Функция убывает на [-1; 1].
Функция непрерывна.
Функция не является ни четной, ни нечетной.
Функция убывает на [-1; 1].
Функция непрерывна.
![Функция y=arccos x и ее свойстваD(y) = [-1; 1].E(y) = [0; π].Функция не является ни четной, ни](/img/thumbs/53be4540e9f40b4fe44acaca2c4e3e3c-800x.jpg "Презентация по математике на тему Обратные тригонометрические функции (10 класс) Функция y=arccos x и ее свойстваD(y) = [-1; 1].E(y) = [0;")
Слайд 9Функция y=arctg x и ее свойства
arctg а – это такое число
из интервала (-π/2; π/2), тангенс которого равен а.
Слайд 11Функция y=arctg x и ее свойства
D(y) = (- ∞; +∞).
E(y) =
(-π/2; π/2).
arctg (-x) = - arctg x – функция нечетная.
Функция возрастает на (- ∞; +∞).
Функция непрерывна.
arctg (-x) = - arctg x – функция нечетная.
Функция возрастает на (- ∞; +∞).
Функция непрерывна.
Слайд 12Функция y=arcсtg x и ее свойства
arcсtg а – это такое число
из интервала (0; π), котангенс которого равен а.
Слайд 14Функция y=arcсtg x и ее свойства
D(y) = (- ∞; +∞).
E(y) =
(0; π).
Функция не является ни четной, ни нечетной.
Функция убывает на (- ∞; +∞).
Функция непрерывна.
Функция не является ни четной, ни нечетной.
Функция убывает на (- ∞; +∞).
Функция непрерывна.
