- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Неравенства второй степени
Содержание
- 1. Презентация по математике на тему Неравенства второй степени
- 2. Неравенства вида ах2 + bх + с
- 3. Итак, для решения неравенств вида
- 4. 1. Определите знаки коэффициентов а и
- 5. Устные упражнения. На рисунках изображен
- 6. Устные упражнения. На рисунках изображен
- 7. 1. Корнями
- 8. 2. Корнями квадратичной функции у =
- 9. 3. Наибольшее или наименьшее значение принимает функция
- 10. 4. Найдите промежуток возрастания функции у =
- 11. 5. Решите неравенство
- 12. ОТВЕТЫ № 1рис. а:
- 13. ОТВЕТЫ № 2Рис. а: а) х
- 14. ОТВЕТЫ № 3Рис.а:
- 15. Д/з№ 117( б)№ 118 (в, д, е)№ 130 (а, в)
Слайд 2
Неравенства вида ах2 + bх + с > 0
где х — переменная, а, b и с — некоторые числа, причем а ≠ 0, называют неравенствами второй степени с одной переменной.
Решение неравенства второй степени с одной переменной можно рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.
Слайд 3 Итак, для решения неравенств вида ах2 + bх + с >
1) находят дискриминант квадратного трехчлена и выясняют, имеет ли трехчлен корни;
2) если трехчлен имеет корни, то отмечают их на оси х и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при а > О или вниз при а < 0; если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а > 0 или в нижней при а < 0;
3) находят на оси х промежутки, для которых точки параболы расположены выше оси х (если решают неравенство ах2 + bх + с > 0 ) или ниже оси х (если решают неравенство ах2 + bх + с < О ).
Слайд 4
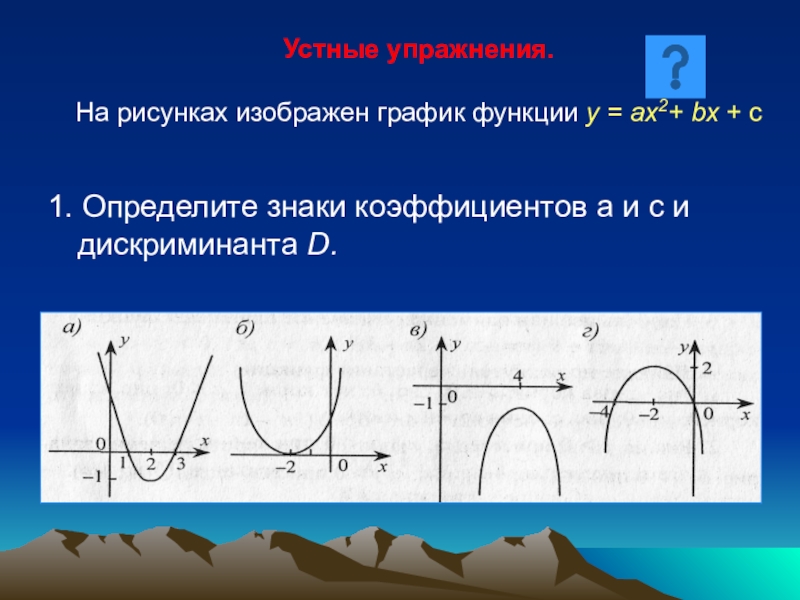
1. Определите знаки коэффициентов а и с и дискриминанта D.
Устные
На рисунках изображен график функции у = ах2+ bх + с
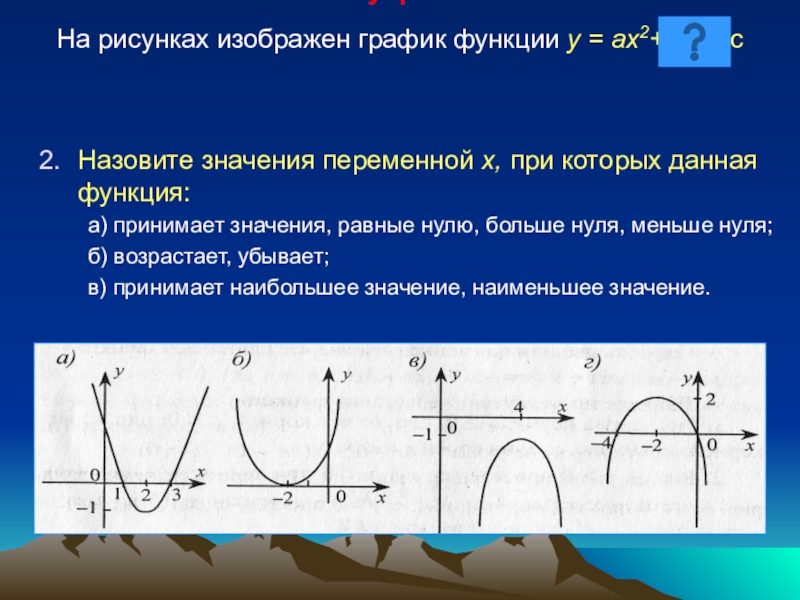
Слайд 5 Устные упражнения. На рисунках изображен график функции у = ах2+ bх
Назовите значения переменной х, при которых данная функция:
а) принимает значения, равные нулю, больше нуля, меньше нуля;
б) возрастает, убывает;
в) принимает наибольшее значение, наименьшее значение.
Слайд 6 Устные упражнения. На рисунках изображен график функции у = ах2+ bх
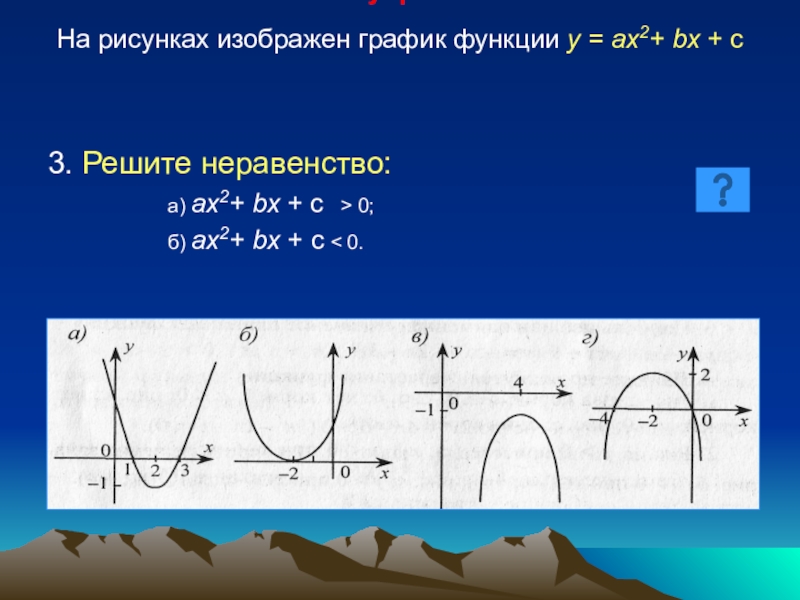
3. Решите неравенство:
а) ах2+ bх + с > 0;
б) ах2+ bх + с < 0.
Слайд 7
1. Корнями квадратичной функции
у = -Зх2 + 6х
Укажите промежуток возрастания функции.
Ответ: (- ∞; -1]
Математический диктант
Слайд 82. Корнями квадратичной функции
у = -Зх2 + 6х
Укажите множество решений неравенства –Зх2 + 6х + 9 < 0
Ответ: (- ∞; -1) U (3;+ ∞)
Математический диктант
Слайд 93. Наибольшее или наименьшее значение принимает функция
Ответ: наибольшее
Математический диктант
Слайд 104. Найдите промежуток возрастания функции у = 2х2 - 4х –
Ответ: [1;+ ∞)
Математический диктант
Слайд 12ОТВЕТЫ № 1
рис. а:
рис. б:
а > 0, с > 0, D = 0;
рис. в:
а<0, с<0, D <0;
рис. г:
а<0, с = 0, D >0.
Слайд 13ОТВЕТЫ № 2
Рис. а:
а) х = 1; 3; х
1 < х < 3;
б) [2; +∞), (- ∞; 2];
в) при х = 2 функция принимает наименьшее значение.
Рис. б:
а) х = -2, (- ∞; -2)U (-2; + ∞);
б) [-2; + ∞), (- ∞; -2];
в) при х = -2 функция принимает наименьшее значение.
Рис. в:
а) у≠ 0, (- ∞; + ∞);
б) (- ∞; 4]; [4; + ∞);
в) при х = 4 функция принимает наибольшее значение.
Рис. г:
а) х = -4; 0; (-4; 0);
(- ∞; -4) U (0; + ∞);
б) (- ∞; -2], [-2; + ∞ );
в) при х= -2 функция принимает наибольшее значение.
Слайд 14ОТВЕТЫ № 3
Рис.а:
а)(-∞; 1)U(3;+ ∞
Рис. б:
а) (- ∞ ; -2)U (-2; + ∞ ); б) нет решений.
Рис. в:
а) нет решений; б) (- ∞; + ∞ ).
Рис. г:
а) (-4; 0); б) (- ∞ ; -4)U (0; + ∞)