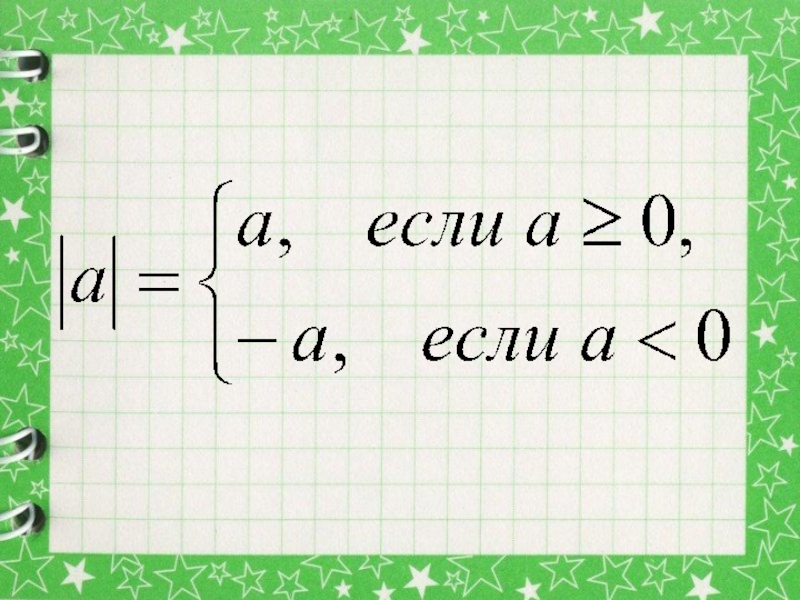- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Модуль числа. Уравнения и неравенства, содержащие модуль
Содержание
- 1. Презентация по математике на тему Модуль числа. Уравнения и неравенства, содержащие модуль
- 2. Заполни пропускиа) |5|=…б) |– 8,3|=…в) | – 1,2| + |– 2,4|=…г) | – 8|·|2,3|=…
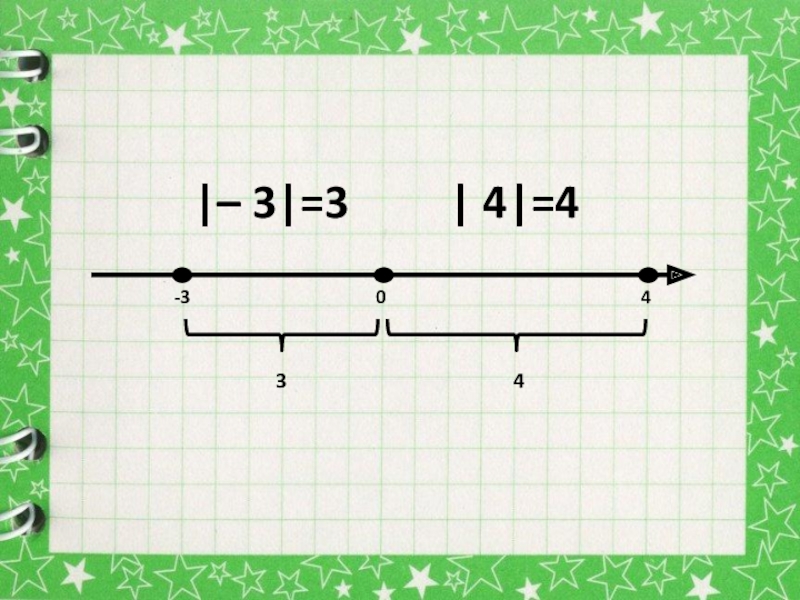
- 3. На каком расстоянии от точки О на
- 4. Назовите числа, модуль которыхравен:86,204) – 6
- 5. Слайд 5
- 6. Слайд 6
- 7. Решим уравнение: |x|=8Решение: |x|=8Ответ: 8, – 8
- 8. Рассмотрим уравнение: |х|=а, если а>0 – а
- 9. Решить уравнение: |2х+3|=1 – 1
- 10. Если а
- 11. Если а=0,то уравнение |х|=а имеет один корень. Запомни!Например:|х|= 0 х=0
- 12. Работа в парах:Решить уравнения:|х|=2,5|х-1|=2|2х-3|=0|4х+2,3|= – 2,125.
- 13. Домашнее задание:§ 10№150(2,4,6)№151(2,4)№152(2,4)№153(2,4,6)
- 14. Слайд 14
- 15. Модуль числа.Неравенства, содержащие модуль.
- 16. Вариант 1.Решить уравнения:|х|=3,1|х-2|=3|3х-6|=0|8х+2|= – 105. |3х-2|=46.
- 17. – а
- 18. Решить неравенство |5 – 4х|< 1 –
- 19. Если а
- 20. Если а=0,то неравенство: |х|≤а имеет единственноерешение. Запомни!Например:|х|≤ 0х=0
- 21. – а
- 22. – 2
- 23. Если а≤0,то решениями неравенства|х|≥а являются все числа Запомни!Например:|х|≥ – 7х – любое число
- 24. Работа в тетрадях:№157(1,3)№160(1,3)Дополнительное задание № 171(3)
- 25. Домашнее задание:§ 10№157(2,4)№160(2,4)№170(2)№171(2)
- 26. Слайд 26
Слайд 9Решить уравнение: |2х+3|=1
– 1
2х + 3 = – 1
2х = – 1 – 3
2х = – 4
х = – 2
2х + 3 = 1
2х = 1 – 3
2х = – 2
х = – 1
Ответ: – 2; 1
Проверка:
|2∙( –2)+3|=1 |2∙(–1)+3|=1
Слайд 12Работа в парах:
Решить уравнения:
|х|=2,5
|х-1|=2
|2х-3|=0
|4х+2,3|= – 2,12
5. |3х-5|=5
6. |-х|=3,4
|5 –
8. |4 – 5х|= 5
9. |х+4|=0
Проверим ответы:
2,5 и – 2,5
3 и – 1
1,5
корней нет
и 0
3,4 и – 3,4
10 и 0
и
– 4
Дополнительно: № 170(4), 171(4), 179(1)
Слайд 16Вариант 1.
Решить уравнения:
|х|=3,1
|х-2|=3
|3х-6|=0
|8х+2|= – 10
5. |3х-2|=4
6. | – х|=2,1
|4
8. |2 – 2х|= 10
|х+8|=0
|4 – 18х|= – 31,6
Вариант 2.
Решить уравнения:
|x|=6,2
|х-4|=6
|4х-1|= – 5
|2х-1|=3
|6 – х|=6
| – х|=4,8
|3 – х|=3
|3 – 3х|=9
|х+6|=0
|6 – 24х|= – 48,2
Слайд 17 – а
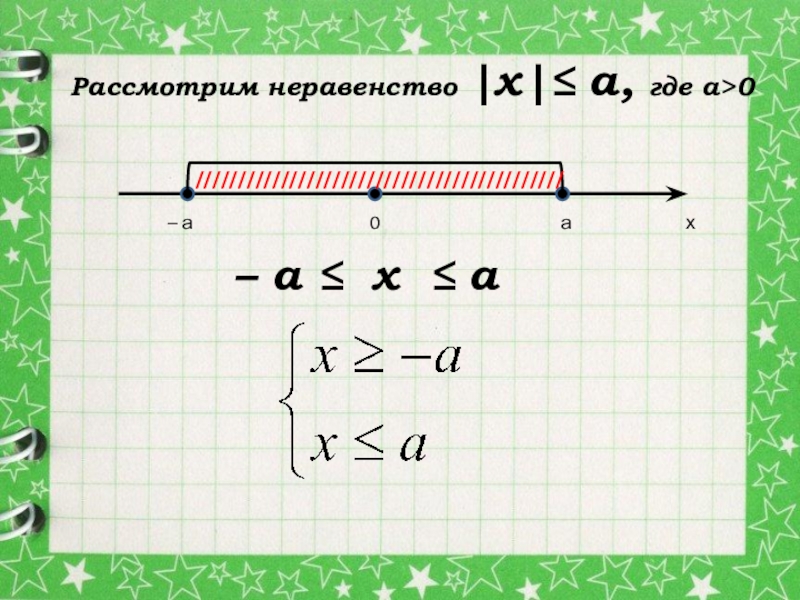
Рассмотрим неравенство |х|≤ а, где а>0
///////////////////////////////////////////
– а ≤ х ≤ а
Слайд 18Решить неравенство |5 – 4х|< 1
– 1
///////////////////////////////////////////
5 – 4x > – 1
– 4x> – 6
x < 1,5
5 – 4x < 1
– 4x< – 4
x > 1
Ответ: (1; 1,5)
Слайд 21 – а
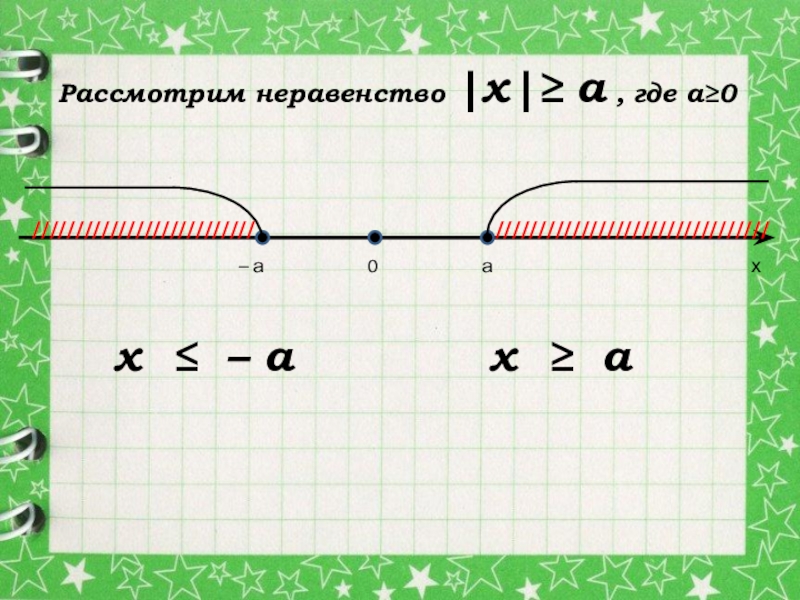
Рассмотрим неравенство |х|≥ а , где а≥0
////////////////////////////////
//////////////////////////
x ≤ – a
x ≥ a
Слайд 22 – 2
Решить неравенство |4х–3|>2
////////////////////////////////
//////////////////////////
4x–3<– 2
4x–3>2
4x<– 2 + 3
4x< 1
x< 0,25
4x>2 + 3
4x> 5
x> 1,25
Ответ: ( – ∞;0,25); (1,25;+ ∞)