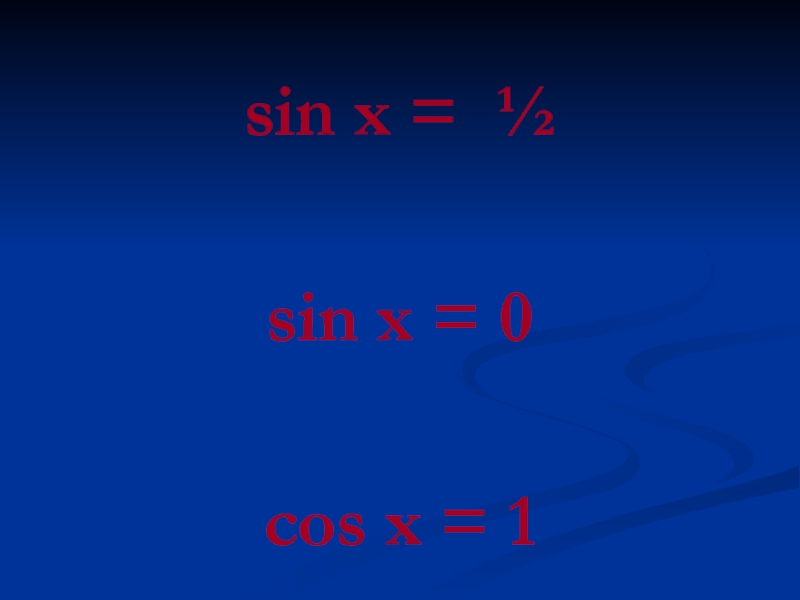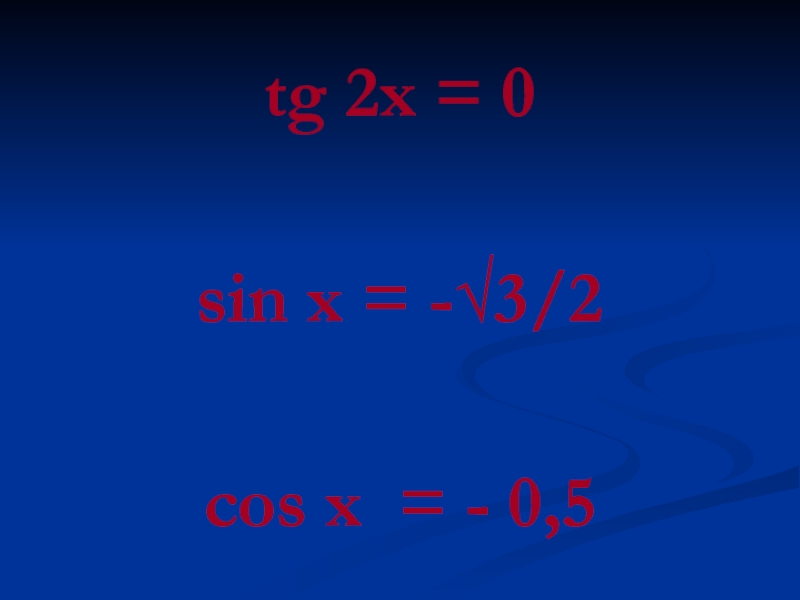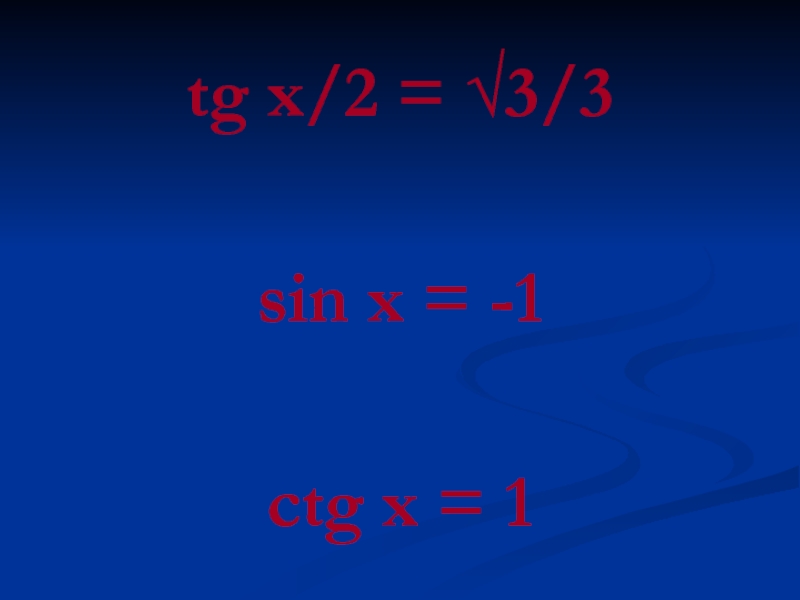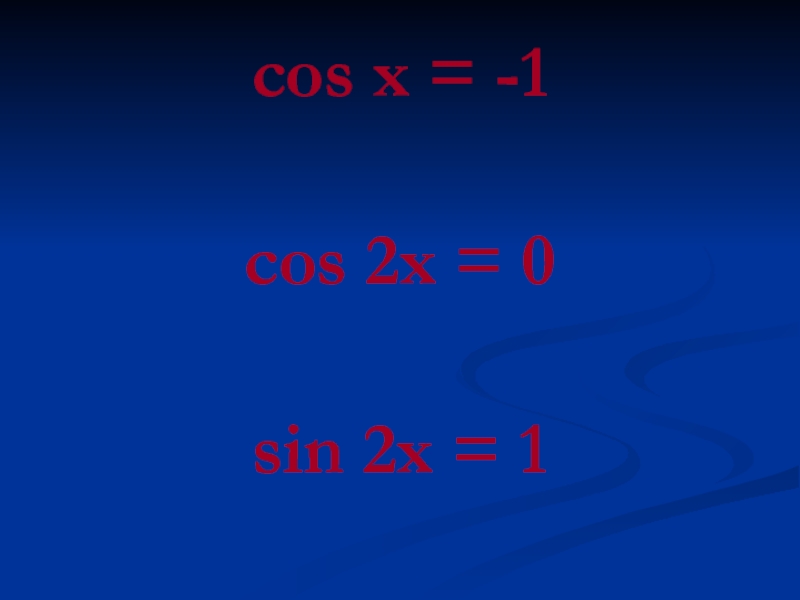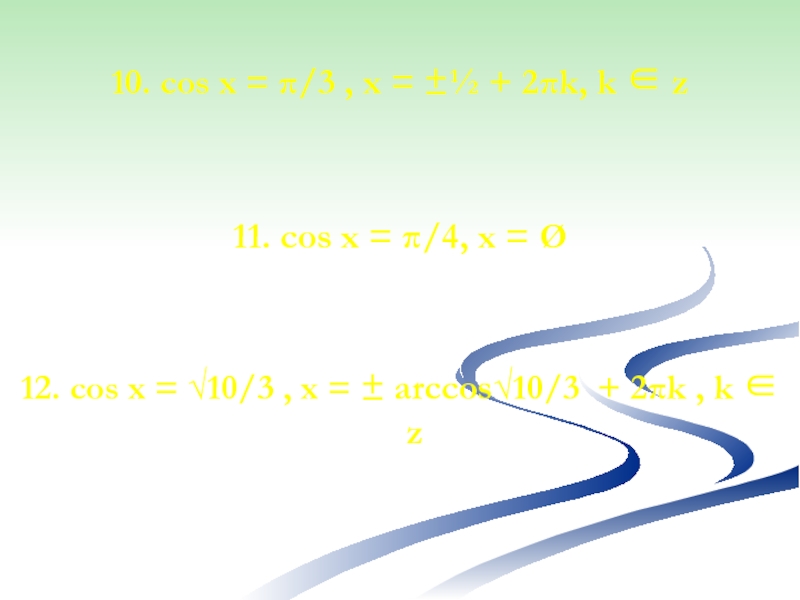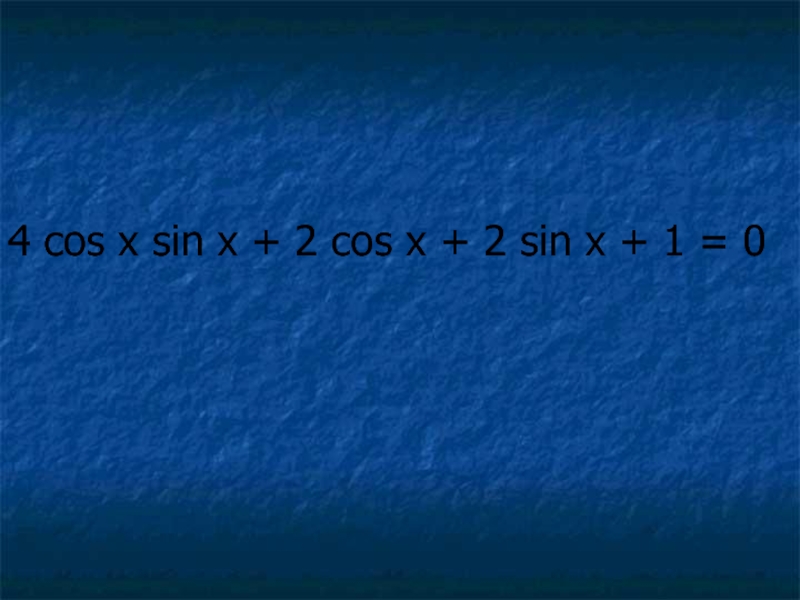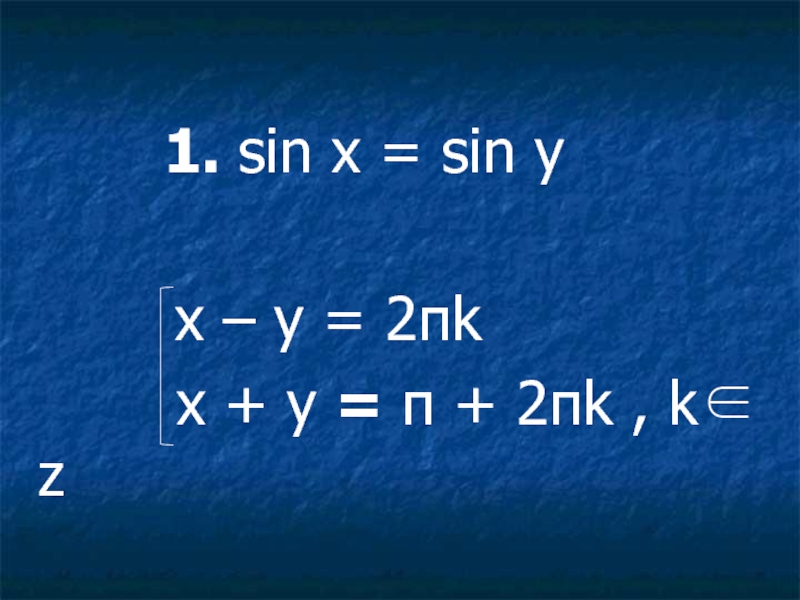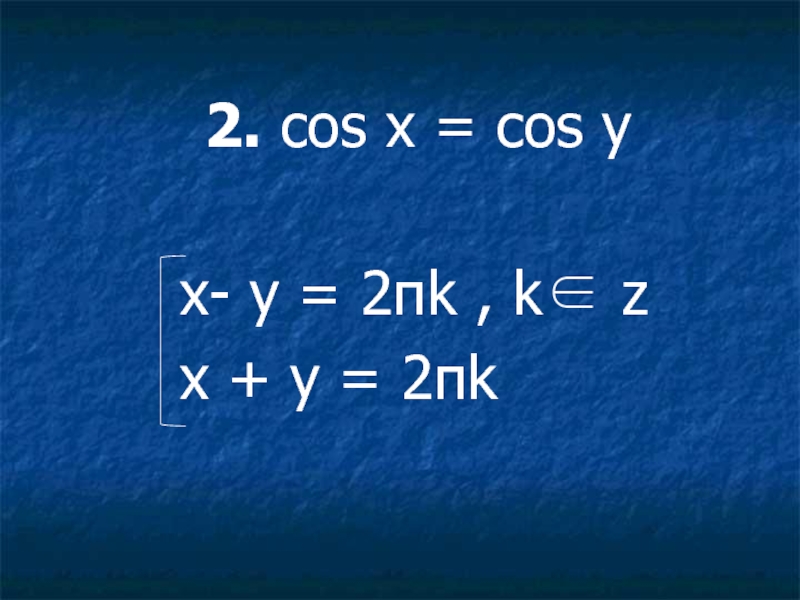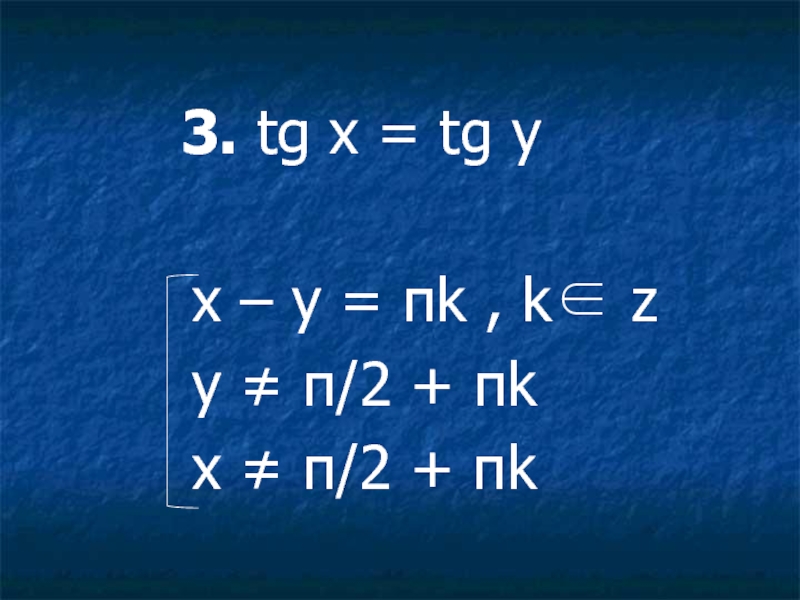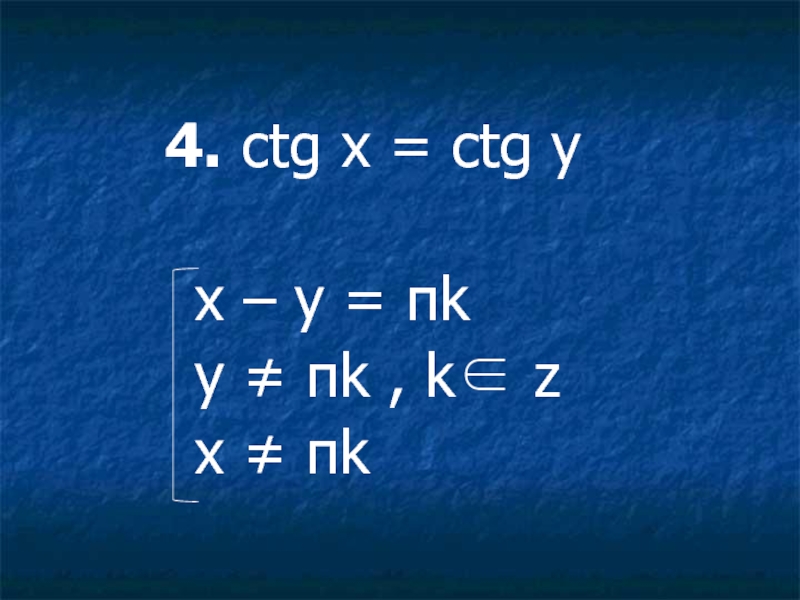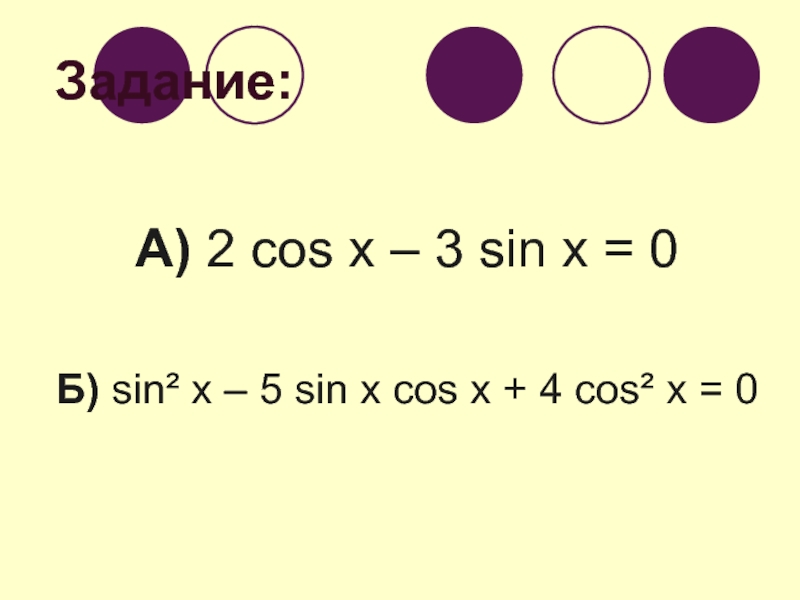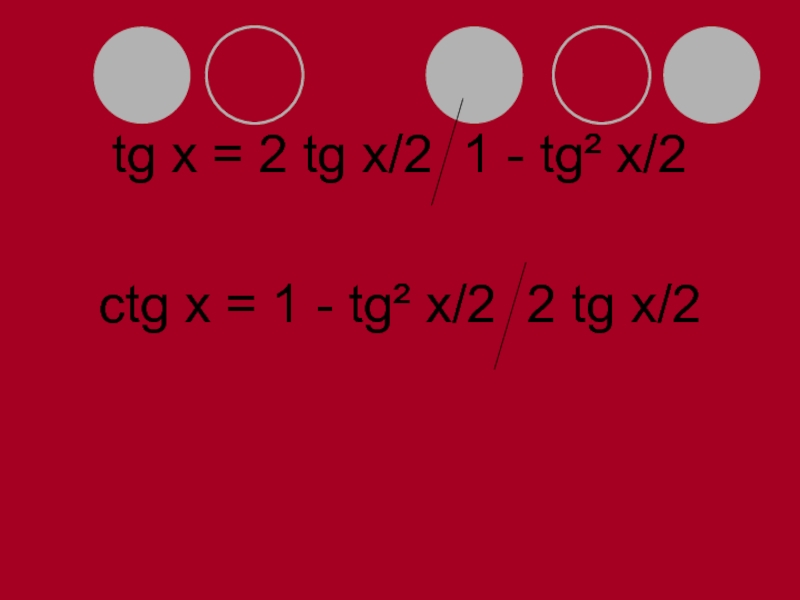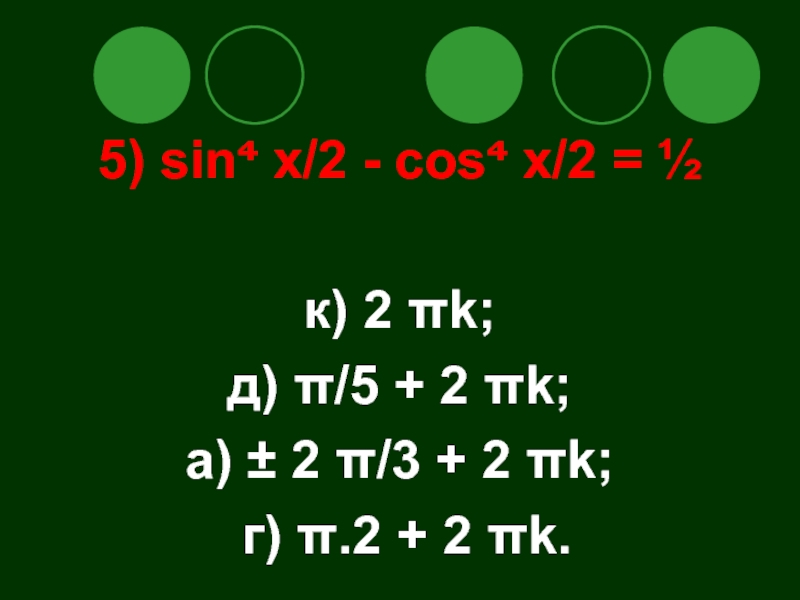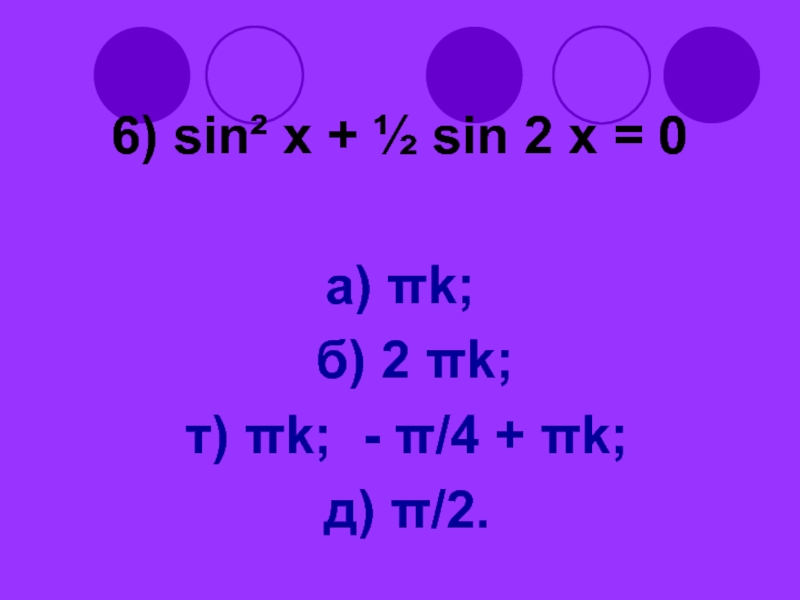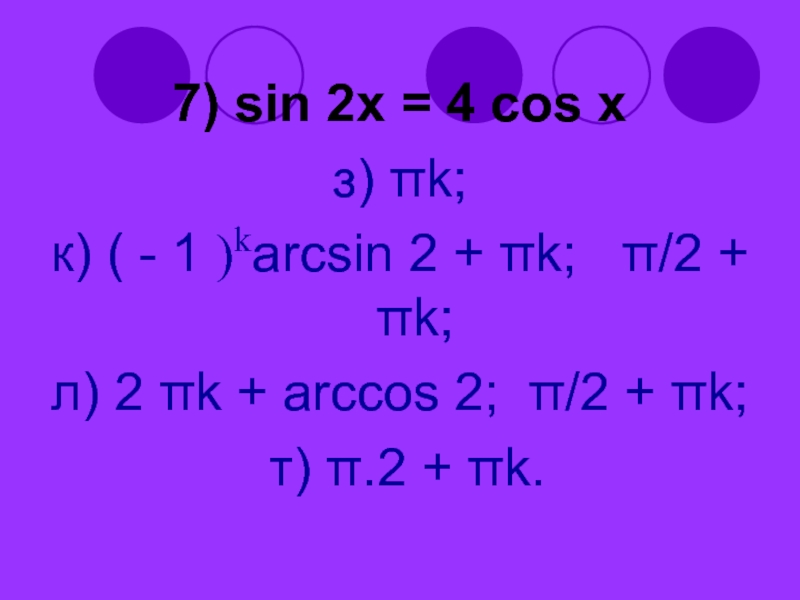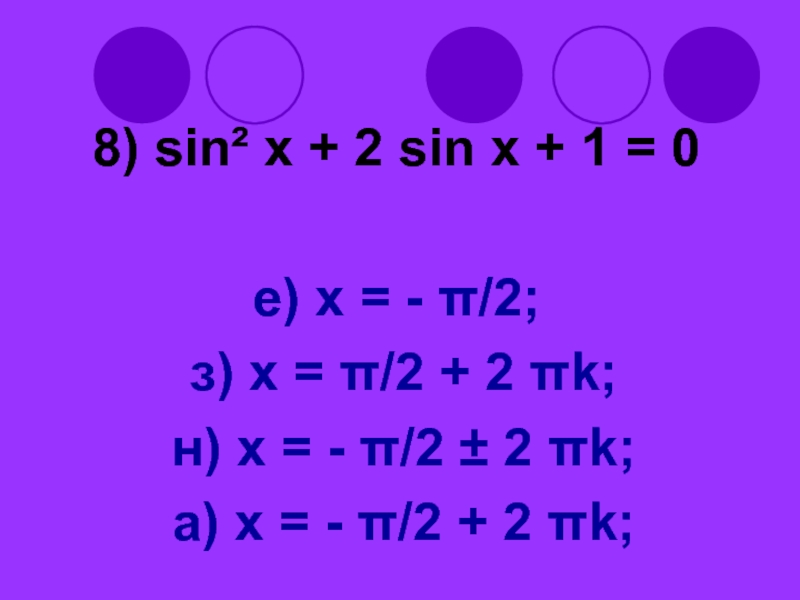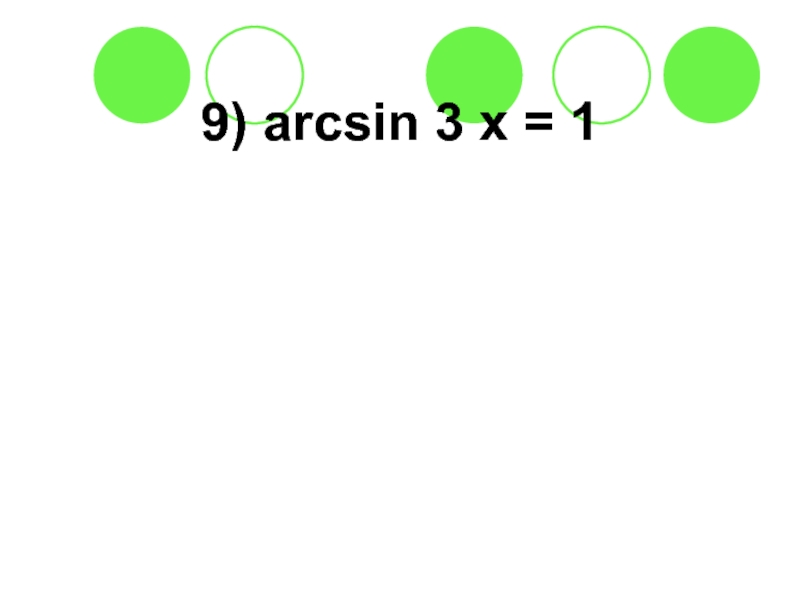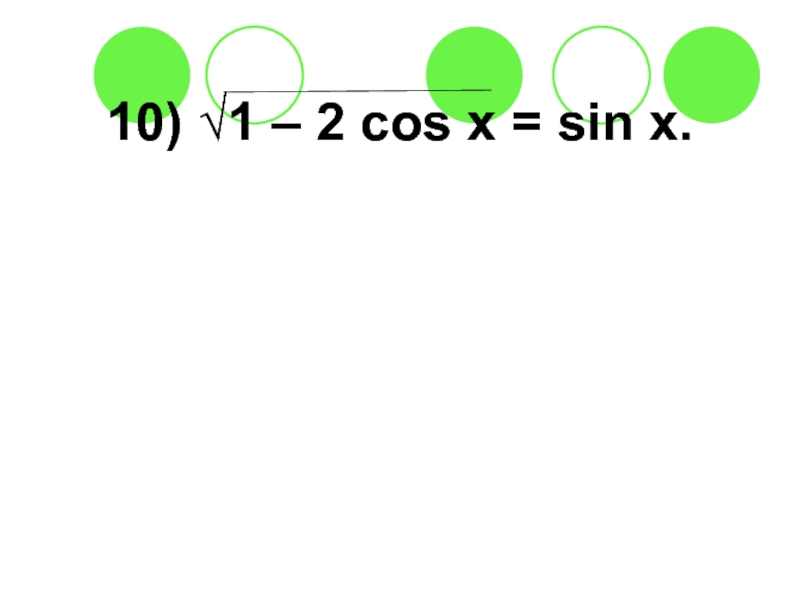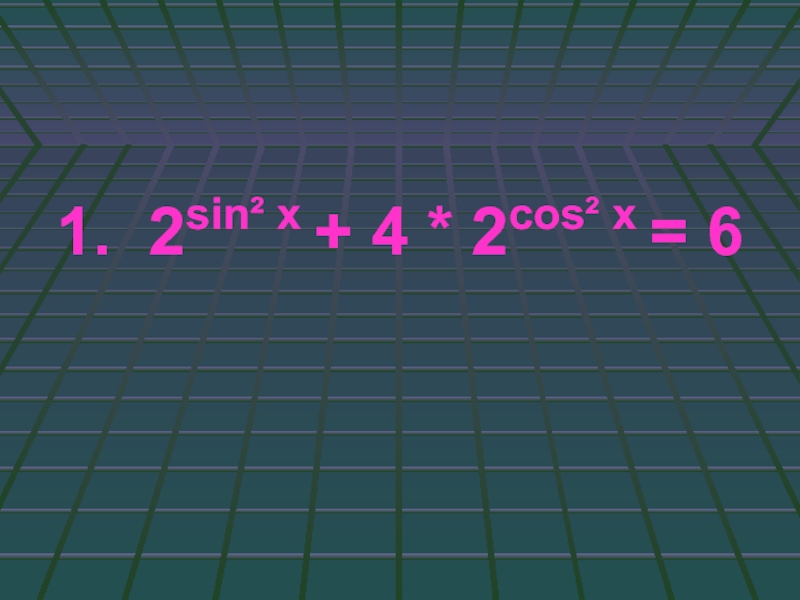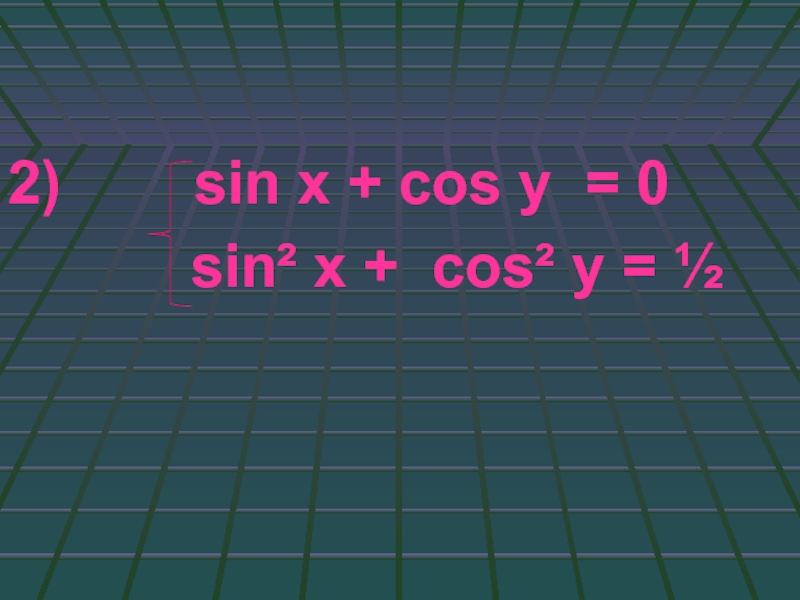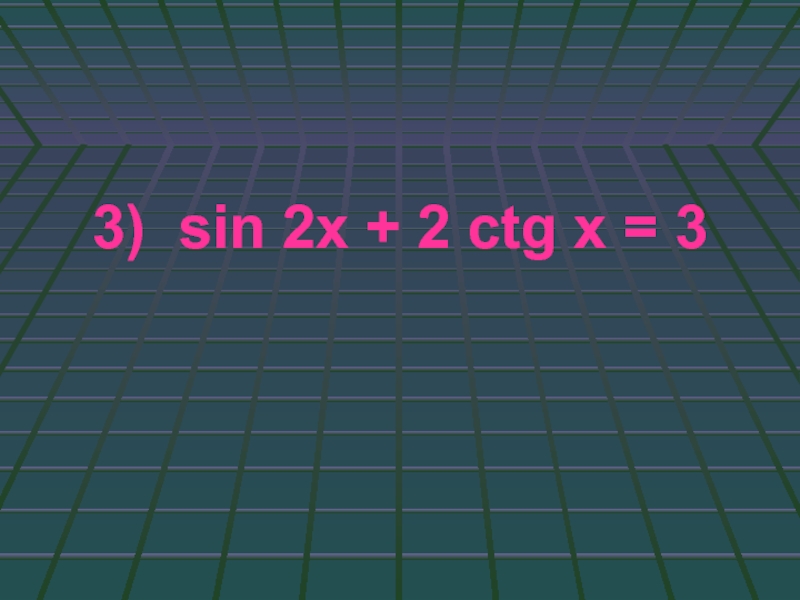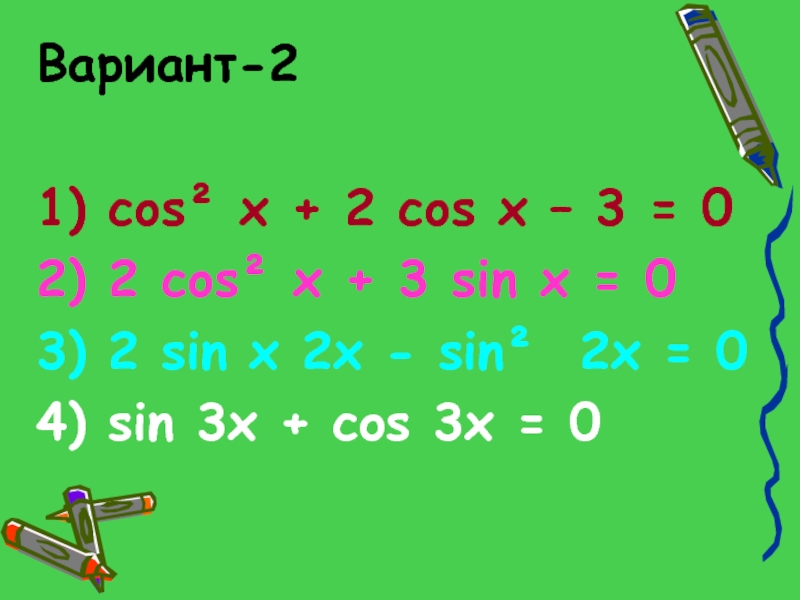- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Методы решения тригонометрических уравнений урок -обобщение
Содержание
- 1. Презентация по математике на тему Методы решения тригонометрических уравнений урок -обобщение
- 2. Высшее назначение математики…Состоит в том, чтобы находить
- 3. Цель занятия:1.Закрепить знания, умения и навыки
- 4. Основные знания и умения Уметь решать несложные тригонометрические уравнения.
- 5. ТСОМультимедиа
- 6. Тип занятия Обобщение и систематизация знаний, умений и навыков.
- 7. I.Фронтальный опрос
- 8. Что значит решить тригонометрическое уравнение?
- 9. Общие решения
- 10. Формулы для решения простейших тригонометрических уравнений
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. II. Устный счет.
- 17. sin x = ½sin x = 0
- 18. tg 2x = 0
- 19. tg x/2 = √3/3
- 20. cos x = -1cos 2x = 0sin 2x = 1
- 21. В каждом из приводимых примеров сделаны ошибки.
- 22. 4.cos x/3 = √2/2 , x =
- 23. 7.sin 2x = 1/3 , x =
- 24. 10. cos x = π/3 , x
- 25. Среди приведенных чисел, укажите те, которые являются
- 26. III. Повторение методов решения
- 27. Тригонометрические уравнения, содержащие одну и ту же
- 28. 3 cos² x/2 – cos x/2 – 2 = 0
- 29. Тригонометрические уравнения, приводящиеся к уравнениям содержащим одну
- 30. 2 sin² x/3 + 5 cos x/3 + 1 = 0
- 31. Тригонометрические уравнения, решающиеся разложением на множители.
- 32. 4 cos x sin x + 2
- 33. Тригонометрические уравнения, решаемые через условия равенства одноименных тригонометрических функций.
- 34. 1. sin
- 35. 2. cos
- 36. 3. tg
- 37. 4. ctg
- 38. Задание: sin ( x + π/3) = sin ( 2x + π/4)
- 39. Однородные тригонометрические уравнения.1) А sin x +
- 40. Задание: А) 2 cos x – 3
- 41. Универсальный метод решения тригонометрических уравнений.cos x =
- 42. tg x = 2 tg x/2 1
- 43. Задание:3 sin x + 4 cos x = 5.
- 44. IV. Историческая справка.
- 45. V.Решение тестовых заданий.
- 46. Задания: 1) 2 sin² x = 1б)
- 47. 2) 1 + cos 2x = 2л)
- 48. 3) tg³ x + tg² x –
- 49. 4) cos 2x = cos 4x б)
- 50. 5) sin x/2 - cos x/2 =
- 51. 6) sin² x + ½ sin 2
- 52. 7) sin 2x = 4 cos xз)
- 53. 8) sin² x + 2 sin x
- 54. 9) arcsin 3 x = 1в) sin
- 55. 10) √1 – 2 cos x =
- 56. VI. Решение задач повышенной сложности.
- 57. 1. 2sin² x + 4 * 2cos² x = 6
- 58. 2) sin x +
- 59. 3) sin 2x + 2 ctg x = 3
- 60. VII. Проверочная работа.
- 61. Вариант-11) 2 sin² x – 3 sin
- 62. Bариант-21) cos² x + 2 cos x
- 63. Bариант-31) tg² x – 4 tg x
- 64. Обобщение. Подведение итогов.
Высшее назначение математики…Состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает. Н. Винер
Слайд 2Высшее назначение математики…
Состоит в том, чтобы находить скрытый порядок в хаосе,
который нас окружает.
Н. Винер
Н. Винер
Слайд 3Цель занятия:
1.Закрепить знания, умения и навыки
решения несложных
тригонометрических уравнений.
2. Воспитывать способность доводить любое учебное задание до конца, правильно оценивать результаты своей работы, усилить внимание к развитию творческого мышления и повышению интереса к предмету.
2. Воспитывать способность доводить любое учебное задание до конца, правильно оценивать результаты своей работы, усилить внимание к развитию творческого мышления и повышению интереса к предмету.
Слайд 21В каждом из приводимых примеров сделаны ошибки. Найдите ошибки.
1. cos
x = ½ , x = ± π/6 , k ∈ z
2. sin x = √3/2 , x = π/3 + πk , k ∈ z
3. tg x = π/4 , x = 1 + πk , k ∈ z
2. sin x = √3/2 , x = π/3 + πk , k ∈ z
3. tg x = π/4 , x = 1 + πk , k ∈ z
Слайд 224.cos x/3 = √2/2 , x = ± 3π /4 +
2 πk/3 , k ∈ z
5.sin 2x = ⅓ ,x =(-½)k arcsin 1/3 + π k , k ∈ z
6.sin 2x = ⅓ , x = ( - 1)k arcsin 1/6 + π k , k ∈ z
5.sin 2x = ⅓ ,x =(-½)k arcsin 1/3 + π k , k ∈ z
6.sin 2x = ⅓ , x = ( - 1)k arcsin 1/6 + π k , k ∈ z
Слайд 237.sin 2x = 1/3 , x = ½ ( - 1
)karcsin 1/3 + π k ,k ∈ z
8. sin 2x = 1/3 , x = ½ ( - 1 )karcsin 1/3 + 2πk, k ∈ z
9. cos x = - ½ , x = ± (- π/3) + 2πk , k ∈ z
8. sin 2x = 1/3 , x = ½ ( - 1 )karcsin 1/3 + 2πk, k ∈ z
9. cos x = - ½ , x = ± (- π/3) + 2πk , k ∈ z
Слайд 2410. cos x = π/3 , x = ±½ + 2πk,
k ∈ z
11. cos x = π/4, x = Ø
12. cos x = √10/3 , x = ± arccos√10/3 + 2πk , k ∈ z
11. cos x = π/4, x = Ø
12. cos x = √10/3 , x = ± arccos√10/3 + 2πk , k ∈ z
Слайд 25Среди приведенных чисел, укажите те, которые являются корнями данного уравнения
1. cos
2x = ½ 2. tg x = √3
π /6; π /3; π/2; 2π/3; 5 π/6; π;
7π/6; 4π/3; 3π/2; 5π/3; 11π/6; 2π
π /6; π /3; π/2; 2π/3; 5 π/6; π;
7π/6; 4π/3; 3π/2; 5π/3; 11π/6; 2π
Слайд 27Тригонометрические уравнения, содержащие одну и ту же функцию одного и того
же аргумента и решается методом подстановки.
Слайд 29
Тригонометрические уравнения, приводящиеся к уравнениям содержащим одну и ту же функцию
одного и того же аргумента и решаемые методом подстановки.
Слайд 33Тригонометрические уравнения, решаемые через условия равенства одноименных тригонометрических функций.
Слайд 39Однородные тригонометрические уравнения.
1) А sin x + B cos x =
0
2) A sin² x + B sin x cos x + C cos² x = 0
2) A sin² x + B sin x cos x + C cos² x = 0
Слайд 41Универсальный метод решения тригонометрических уравнений.
cos x = 1 - tg² x/2
1 + tg² x/2
sin x = 2 tg x/2 1+ tg² x/2
sin x = 2 tg x/2 1+ tg² x/2
Слайд 46Задания:
1) 2 sin² x = 1
б) π/3 + πk;
а) (- 1 )k π/4 + πk; (- 1 )k + 1 π/4 + πk
в) π/3 + 2 πk.
в) π/3 + 2 πk.
Слайд 527) sin 2x = 4 cos x
з) πk;
к) (
- 1 )karcsin 2 + πk; π/2 + πk;
л) 2 πk + arccos 2; π/2 + πk;
т) π.2 + πk.
л) 2 πk + arccos 2; π/2 + πk;
т) π.2 + πk.
Слайд 538) sin² x + 2 sin x + 1 = 0
е)
x = - π/2;
з) x = π/2 + 2 πk;
н) x = - π/2 ± 2 πk;
а) x = - π/2 + 2 πk;
з) x = π/2 + 2 πk;
н) x = - π/2 ± 2 πk;
а) x = - π/2 + 2 πk;
Слайд 5510) √1 – 2 cos x = sin x.
в) π/2 +
πk;
и) π/2 + 2 πk;
з) π/2 + πk; ± arcos 2 + 2 πk;
д) 2 πk.
и) π/2 + 2 πk;
з) π/2 + πk; ± arcos 2 + 2 πk;
д) 2 πk.
Слайд 61Вариант-1
1) 2 sin² x – 3 sin x + 1 =
0
2) 3 cos x = 2 sin² x
3) cos² x – cos x = 0
4) sin x – cos x = 0
2) 3 cos x = 2 sin² x
3) cos² x – cos x = 0
4) sin x – cos x = 0
Слайд 62Bариант-2
1) cos² x + 2 cos x – 3 = 0
2)
2 cos² x + 3 sin x = 0
3) 2 sin x 2x - sin² 2x = 0
4) sin 3x + cos 3x = 0
3) 2 sin x 2x - sin² 2x = 0
4) sin 3x + cos 3x = 0
Слайд 63Bариант-3
1) tg² x – 4 tg x + 3 = 0
2)
cos x - sin x = sin x
3) sin x * tg x/2 = 0
4) √3 sin 2x + 3 cos 2x = 0
3) sin x * tg x/2 = 0
4) √3 sin 2x + 3 cos 2x = 0