Презентация, доклад по математике на тему Метод математической индукции (10 класс)

Содержание

Полная индукция — метод доказательства, при котором утверждение доказывается для конечного числа частных случаев, исчерпывающих все возможности.Неполная индукция — наблюдения за отдельными частными случаями наводит на гипотезу, которая нуждается в доказательстве.

Слайд 1
ИНДУ́КЦИЯ (Женский род)
(из лат. inductio «выведение, наведение»)
способ рассуждения от частных фактов, положений

к общим выводам
ИНДУ́КЦИЯ (Женский род) (из лат. inductio «выведение, наведение») способ рассуждения от частных фактов, положений к общим выводам

Слайд 2Полная индукция — метод доказательства, при котором утверждение доказывается для конечного числа

частных случаев, исчерпывающих все возможности.
Неполная индукция — наблюдения за отдельными частными случаями наводит на гипотезу, которая нуждается в доказательстве.

Полная индукция — метод доказательства, при котором утверждение доказывается для конечного числа частных случаев, исчерпывающих все возможности.Неполная индукция —

Слайд 3Принцип математической индукции
Если предложение А(n), зависящее от натурального числа

n, истинно для n=1 и из того, что оно истинно для n=k (где k-любое натуральное число), следует, что оно истинно и для следующего числа n=k+1, то предположение А(n) истинно для любого натурального числа n.

Принцип математической индукции Если предложение А(n), зависящее от натурального числа n, истинно для n=1 и

Слайд 5Метод математической индукции
Пусть нужно доказать справедливость некоторого математического высказывания

на множестве натуральных чисел.
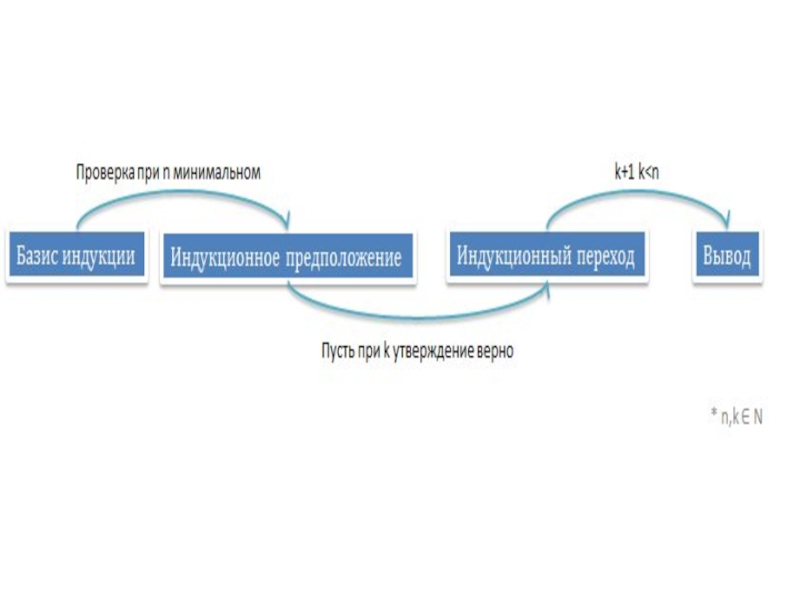
1) Проверка утверждения для n=1 (минимального значения n) (Базис Индукции)
2) Предполагают, что данное утверждение справедливо при k натуральных чисел (k3) Проверяют справедливость данного утверждения при n=k+1.
Если n=k+1 справедливо, то считается, что данное утверждение справедливо для всех натуральных n (Индукционный переход)

Метод математической индукции Пусть нужно доказать справедливость некоторого математического высказывания на множестве натуральных чисел.1) Проверка утверждения

Слайд 7Недостатки метода:
Доказывать тождество можно только на множестве натуральных чисел
Доказывать тождество можно

только для одной переменной

Недостатки метода: Доказывать тождество можно только на множестве натуральных чиселДоказывать тождество можно только для одной переменной
Скачать презентацию

Похожие презентации

Презентация по алгебре Решение показательных уравнений Презентация по алгебре Решение показательных уравнений 204
Презентация внеурочного занятия по математике для учащихся 7-9 классов Презентация внеурочного занятия по математике для учащихся 7-9 классов 250
Презентация к уроку алгебры в 8 классе Степень с целым отрицательным показателем. Презентация к уроку алгебры в 8 классе Степень с целым отрицательным показателем. 447
Презентация по теме: Решение задач на концентрацию, сплавы, движение (9-11 классы) Презентация по теме: Решение задач на концентрацию, сплавы, движение (9-11 классы) 265
Презентация по математике для 8-9 класса Решение неполных квадратных уравнений Презентация по математике для 8-9 класса Решение неполных квадратных уравнений 273
Презентация по математике Линейная функция, её свойства и график 7 класс Презентация по математике Линейная функция, её свойства и график 7 класс 217

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Яндекс.Метрика

Обратная связь

Email: Нажмите что бы посмотреть