- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Метод интервалов (11 класс)
Содержание
- 1. Презентация по математике на тему Метод интервалов (11 класс)
- 2. Теоретическая основа методаПусть задана функция f(x), тогда
- 3. Методом интервалов можно решать неравенства вида: f(х)>0 , f(х)0 f(х)
- 4. 2. f(x)=0 11. ОДЗ неравенства 3. На числовой прямой: 4. Определить знак f(x):5. Записать ответРЕШЕНИЕ:РЕШИТЬ НЕРАВЕНСТВО:
- 5. 21. ОДЗ:Решение.+_+2.3.2. Решаем уравнениеВходят в ОДЗ.3. На
- 6. Неравенства ЕГЭ-15 после замены переменной сводились к
- 7. Метод интервалов для рациональных неравенств
- 8. 3Решение.1. ОДЗ:2. Решаем уравнение:
- 9. 3. На ОДЗ создаём интервалы, проставляем знаки, выбираем ответ:Первый знак:_Смена знака:ммннм++__+Выбор ответа:Ответ:
- 10. tt41. ОДЗ:2. Решаем уравнение:Решение.Замена:tтогдаt2Входят в ОДЗ.
- 11. 3. На ОДЗ создаём интервалы, проставляем знаки, выбираем ответ:Первый знак:Смена знака:Выбор ответа:+нм_ммм++_+Ответ:
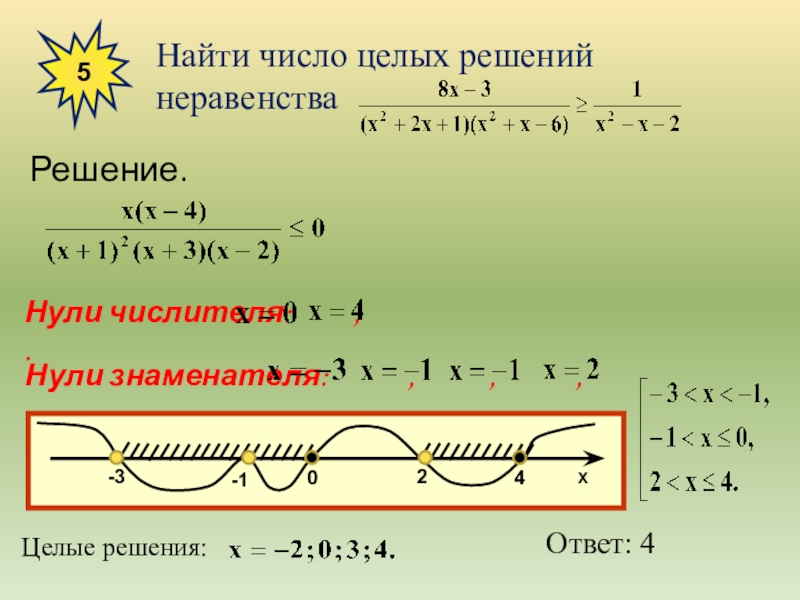
- 12. 5Решение.Нули числителя: ,
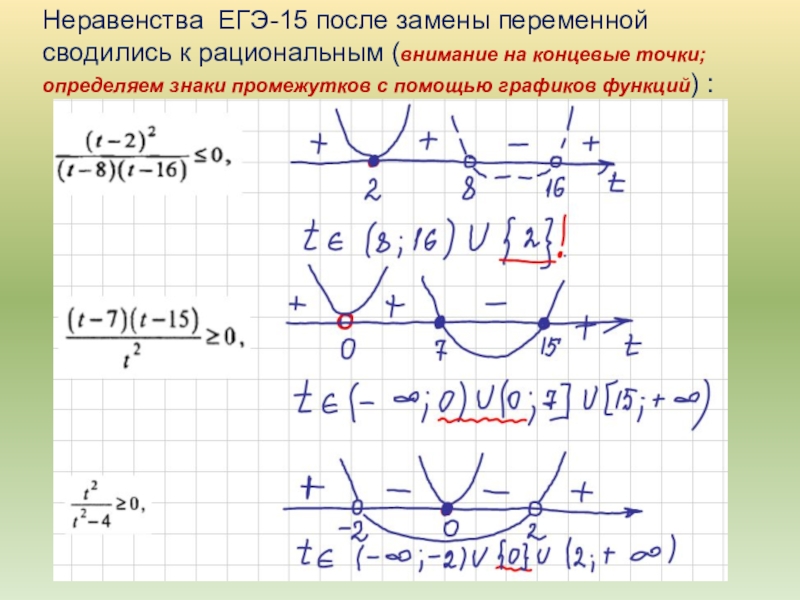
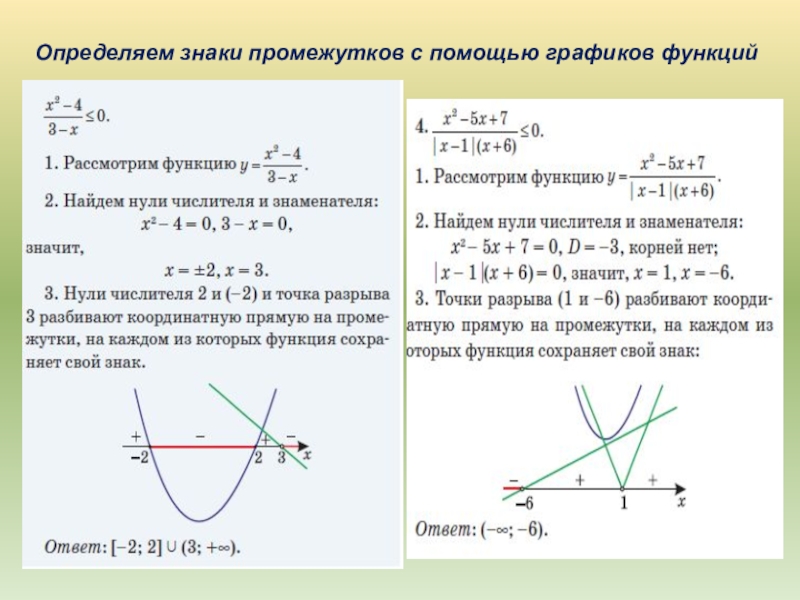
- 13. Определяем знаки промежутков с помощью графиков функций
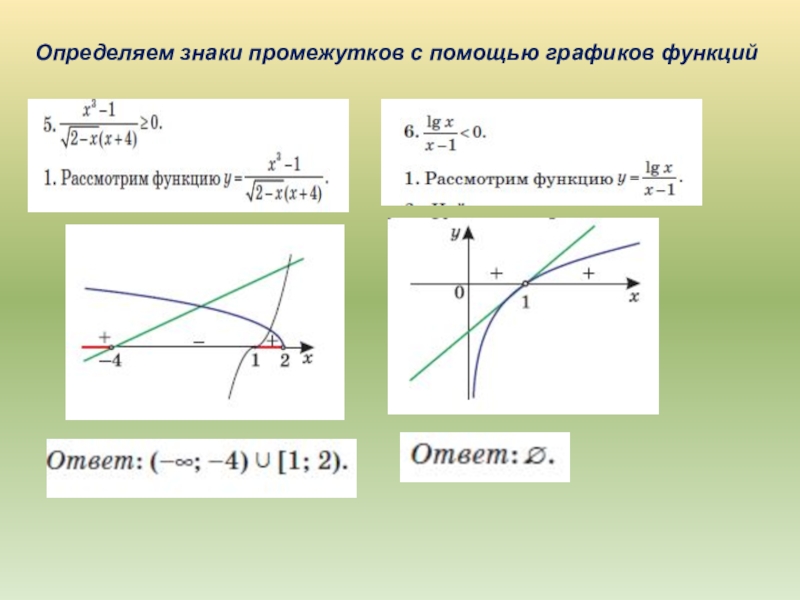
- 14. Определяем знаки промежутков с помощью графиков функций
- 15. Литература: http://alexlarin.net/ege/2011/C3-2011.htmlhttp://office.microsoft.com/ru-ru/clipart/results.aspx?qu=%D1%81%D0%BC%D0%B0%D0%B9%D0%BB%D0%B8%D0%BA&sc=20#48http://reshuege.ru/test?theme=242https://my.webinar.ru/record/714753 (вебинар «Метод интервалов» Лахова Н.В.,
Слайд 2Теоретическая основа метода
Пусть задана функция f(x), тогда числовую прямую (значения х)
А- множество точек, для которых f(x)>0
B- множество точек, для которых f(x)=0
C- множество точек, для которых f(x)<0
D- множество точек, для которых f(x) не определена
ТЕОРЕМА :
Если функция f непрерывна на интервале (a;b)
и не обращается в 0 на этом интервале,
то f сохраняет на нём постоянный знак
Необходимым условием смены знака в точке С является : f (c)=0
Однако , это не является достаточным условием : функция f может и не менять своего знака при переходе через точку С
Слайд 3Методом интервалов
можно решать неравенства вида:
f(х)>0 , f(х)0 f(х)
Алгоритм (метод интервалов) :
1. Найти ОДЗ неравенства (область определения функции f )
2. Решить уравнение f(x)=0 (нули функции f )
3. Отметить на числовой прямой:
-ОДЗ (штриховкой)
-корни уравнения из п2 (o, если <,>
●, если ≤,≥)
Все точки разбивают ОДЗ на интервалы
4. Определить знак f(x) в каждом промежутке (подстановкой)
5. Записать ответ. (Внимание на точки, стоящие в концах промежутков)
Слайд 42. f(x)=0
1
1. ОДЗ неравенства
3. На числовой прямой:
4. Определить
5. Записать ответ
РЕШЕНИЕ:
РЕШИТЬ НЕРАВЕНСТВО:
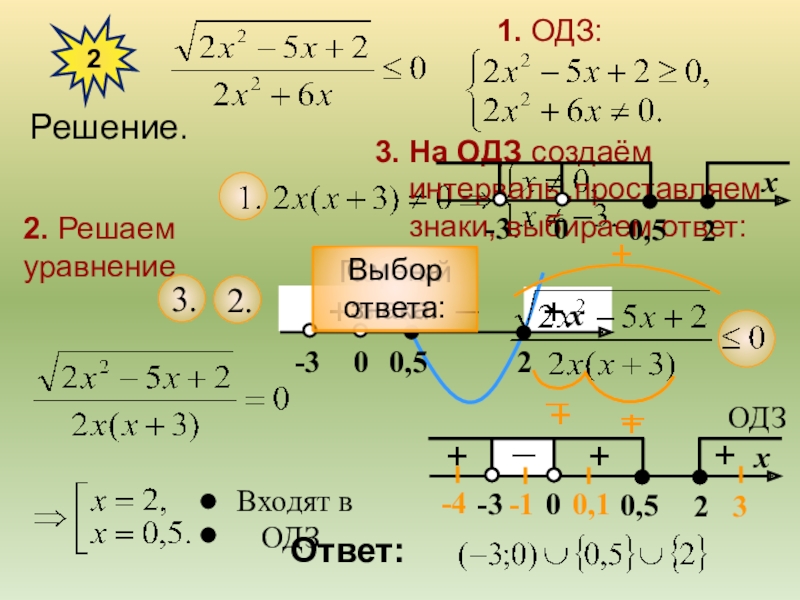
Слайд 52
1. ОДЗ:
Решение.
+
_
+
2.
3.
2. Решаем уравнение
Входят в ОДЗ.
3. На ОДЗ создаём
интервалы,проставляем
знаки, выбираем ответ:
Первый знак:
Смена знака:
Выбор ответа:
ОДЗ
+
+
_
+
Ответ:
Слайд 6Неравенства ЕГЭ-15 после замены переменной сводились к рациональным (внимание на концевые
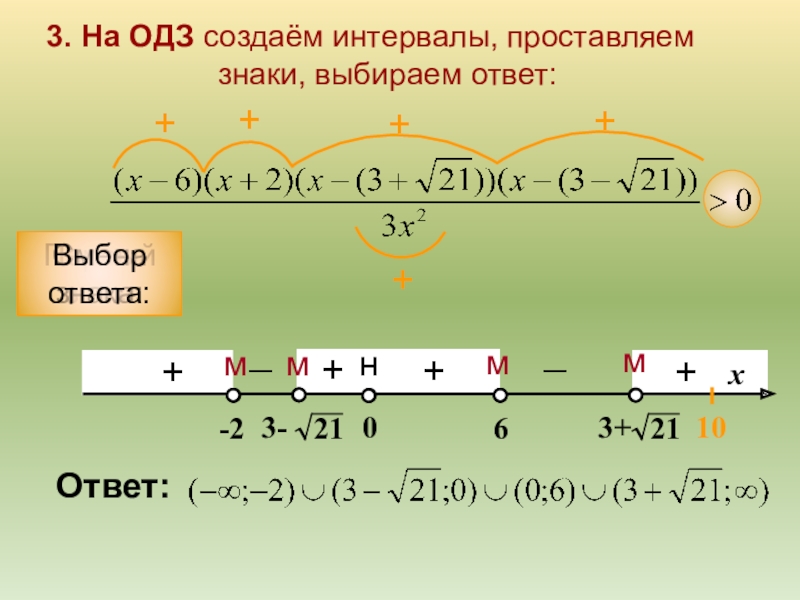
Слайд 93. На ОДЗ создаём интервалы, проставляем
знаки, выбираем ответ:
Первый
_
Смена знака:
м
м
н
н
м
+
+
_
_
+
Выбор ответа:
Ответ:
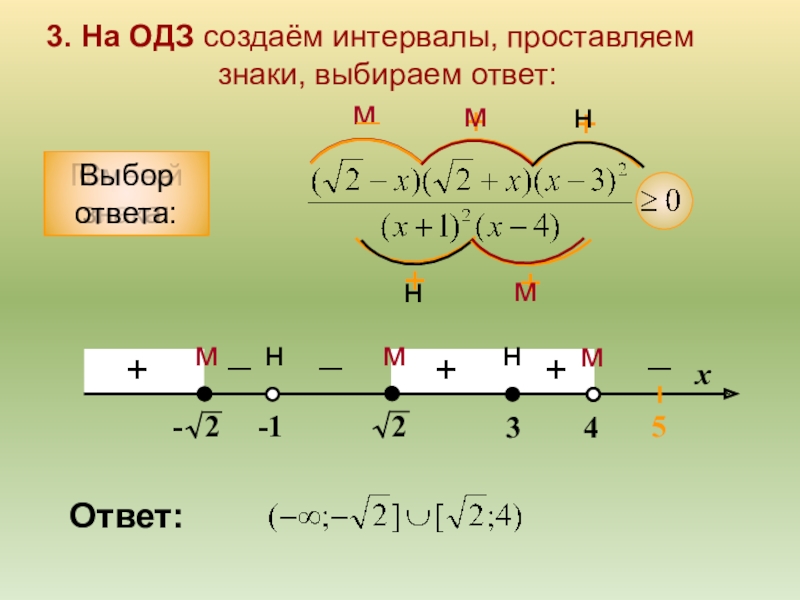
Слайд 113. На ОДЗ создаём интервалы, проставляем
знаки, выбираем ответ:
Первый
Смена знака:
Выбор ответа:
+
н
м
_
м
м
м
+
+
_
+
Ответ:
Слайд 15Литература:
http://alexlarin.net/ege/2011/C3-2011.html
http://office.microsoft.com/ru-ru/clipart/results.aspx?qu=%D1%81%D0%BC%D0%B0%D0%B9%D0%BB%D0%B8%D0%BA&sc=20#48
http://reshuege.ru/test?theme=242
https://my.webinar.ru/record/714753 (вебинар «Метод интервалов» Лахова Н.В., изд-во ПРОСВЕЩЕНИЕ)
Сергеев И. Н.,
Колесникова С. И. Математика. Интенсивный курс подготовки к Единому государственному экзамену / С. И. Колесникова. – 6-е изд. – М.:Айрис-пресс, 2008. – (Домашний репетитор: Подготовка к ЕГЭ)
Оргина Е. Метод интервалов и графики функций. Математика. Методический журнал для учителей математики №5, 2012.
Интернет-ресурсы: