- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Квадратный трёхчлен. Выделение полного квадрата (9 класс)
Содержание
- 1. Презентация по математике на тему Квадратный трёхчлен. Выделение полного квадрата (9 класс)
- 2. Вспомните формулу квадрата разности и квадрата суммы.Сформулируйте
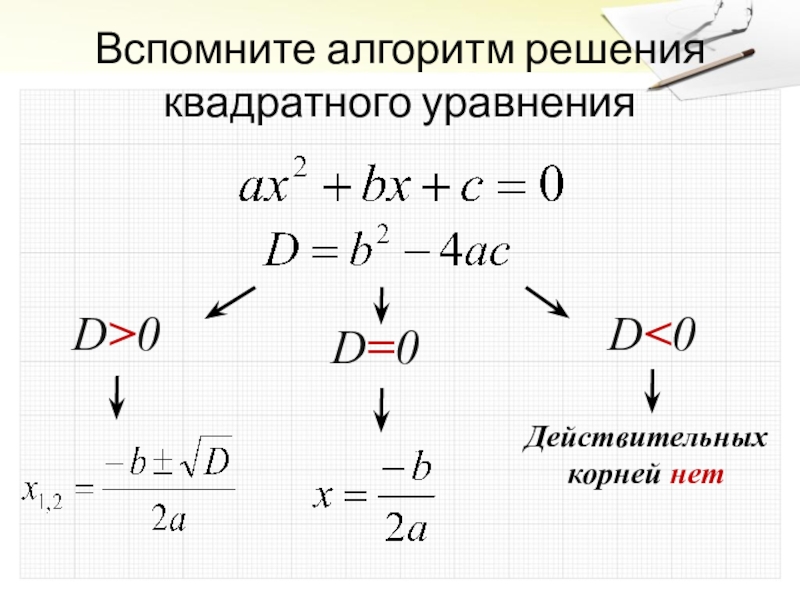
- 3. Вспомните алгоритм решения квадратного уравненияD>0D=0D
- 4. Рассмотрите выражения1. 2. 3. 4. Сколько слагаемых содержит каждое из них?Назовите старшую степень каждого выражения
- 5. Изучаемые определенияКвадратным трёхчленом называется многочлен вида
- 6. Следует обратить внимание!Квадратными трёхчленами также являются:аx2+с (отсутствует
- 7. Преобразуем выражение в скобках также, как
- 8. Разложение на множителиКоэффициент при старшей степени вынесем
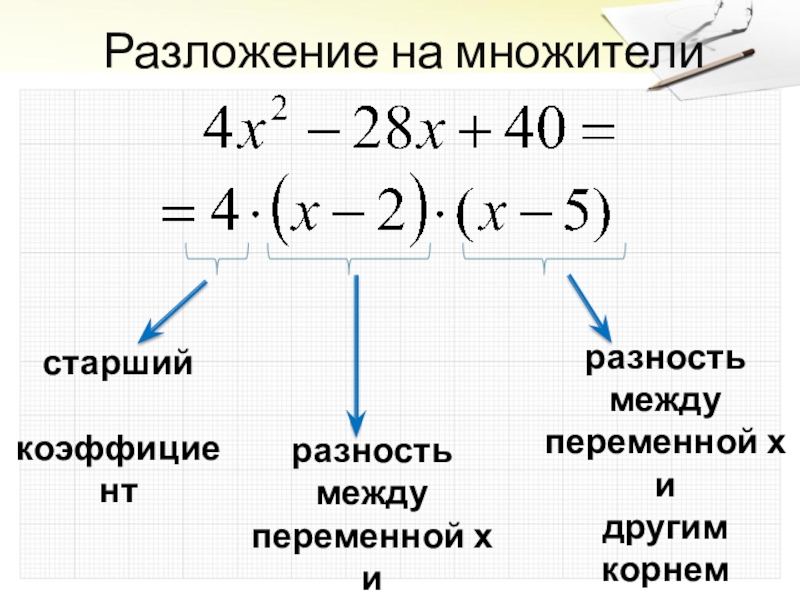
- 9. Разложение на множителистарший коэффициентразность междупеременной х и1м корнемразность междупеременной х идругим корнем
- 10. ТеоремаЕсли и
- 11. Решение задач1. Докажите, что при любом значении
- 12. Решение задачДокажите, что при любом значении квадратный
- 13. 2. Даны квадратные трёхчлены
- 14. В числителе и знаменателе получили одинаковыемножители. Сократим
- 15. Решение задач 3. Сократите дробь б)
- 16. Домашнее заданиеПараграф 2, пункт 3 (стр.22-24),
- 17. Спасибо за урок!
Слайд 1Квадратный трёхчлен. Разложение квадратного трёхчлена на множители
Учитель:
Нестерук Анна Романовна
Слайд 2Вспомните формулу квадрата разности и квадрата суммы.
Сформулируйте теорему Виета
Если числа m
равна –p, а произведение равно q, то эти
числа являются корнями уравнения
Повторение
Слайд 4Рассмотрите выражения
1.
2.
3.
4.
Сколько слагаемых содержит каждое из них?
Назовите
Слайд 5Изучаемые определения
Квадратным трёхчленом называется многочлен вида
Корнем квадратного трёхчлена называется значение
где х - переменная, а,b,c – некоторые числа,
причём а≠0
Слайд 6Следует обратить внимание!
Квадратными трёхчленами также являются:
аx2+с
(отсутствует коэфф. b)
аx2+bx
(отсутствует коэфф.
аx2
(отсутствует коэфф. b и c)
Слайд 7Преобразуем выражение в скобках также,
как в примере1:
Затем прибавим и вычтем
Выделение квадратного двучлена
Выделите квадрат двучлена:
ax2+bx+c
a∙(x-m)2+n
x2+4x+1
Представим 4x в виде произведения:
2
x
Затем прибавим и вычтем :
x2+4x+1= x2+2∙2∙x+22-22+1
=
= (x+2)2 -3
4x=2∙2∙х
2x2-4x+9
Коэффициент при старшей степени вынесем за скобки:
2x2-4x+9=
2
=
=
=
=2(x-1)2+7
x2+3x – 1
Представим 3x в виде произведения:
2
x
x2+3x – 1 = x2+2∙ ∙x+ - +1
=
Слайд 8Разложение на множители
Коэффициент при старшей степени вынесем за скобки:
4x2-28x+40=
4
(x2-7x+10)
Представим -7х в
и применим способ группировки:
4(x2-7x+10)=4(x2-2x-5х+10)=
=4(х(x-2)-5(х-2))
=4(x-2)(х-5)
При х=2 и х=5 произведение, а следовательно,
и трёхчлен 4x2-28x+40 обращаются в нуль.
Значит, числа 2 и 5 являются его корнями.
Слайд 9Разложение на множители
старший
коэффициент
разность между
переменной х и
1м корнем
разность между
переменной х и
другим
Слайд 10Теорема
Если и - корни квадратного
Если D=0, то квадратный трёхчлен
имеет 2 одинаковых корня
Слайд 11Решение задач
1. Докажите, что при любом значении х квадратный трёхчлен:
а)
Решение:
Слайд 12Решение задач
Докажите, что при любом значении квадратный трёхчлен:
б)
в) принимает неположительное значение
г) принимает отрицательное значение
Слайд 132. Даны квадратные трёхчлены
3. Сократите дробь
а) б) в)
Решение задач
Слайд 14В числителе и знаменателе получили одинаковые
множители. Сократим дробь.
Найдём корни трёхчлена в
Разложим трёхчлен на множители
Внесём 5 в числителе в первый множитель
Решение задач
3. Сократите дробь
а)
=