- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Квадрат тигезләмәләрне чишү(8 класс)
Содержание
- 1. Презентация по математике на тему Квадрат тигезләмәләрне чишү(8 класс)
- 2. рәвешендәге тигезләмә квадрат тигезләмә дип атала, биредә х-үзгәрешле, a,b һәм с – ниндидер саннар,өстәвенә Билгеләмә
- 3. а) 6х2 – х + 4 =
- 4. ТУЛЫ БУЛГАН КВАДРАТ ТИГЕЗЛӘМӘТУЛЫ БУЛМАГАН КВАДРАТ ТИГЕЗЛӘМӘКВАДРАТ
- 5. ЧИШҮТУЛЫ БУЛМАГАН КВАДРАТ ТИГЕЗЛӘМӘв=0ах2+с=0с=0ах2+вх=0в,с=0ах2=0 1.Перенос с в
- 6. МӨСТӘКЫЙЛЬ ЭШЛӘ :1 вариант:а) 2х + х2=
- 7. ҖАВАПЛАР 1 вариант:а) 2х + х2= 0
- 8. Тулы булган квадрат тигезләмәләрне чишү ысулларыИке буынның
- 9. Тигезләмәне чишегез:Икебуыннын квадратын аерып чыгару юлы белән
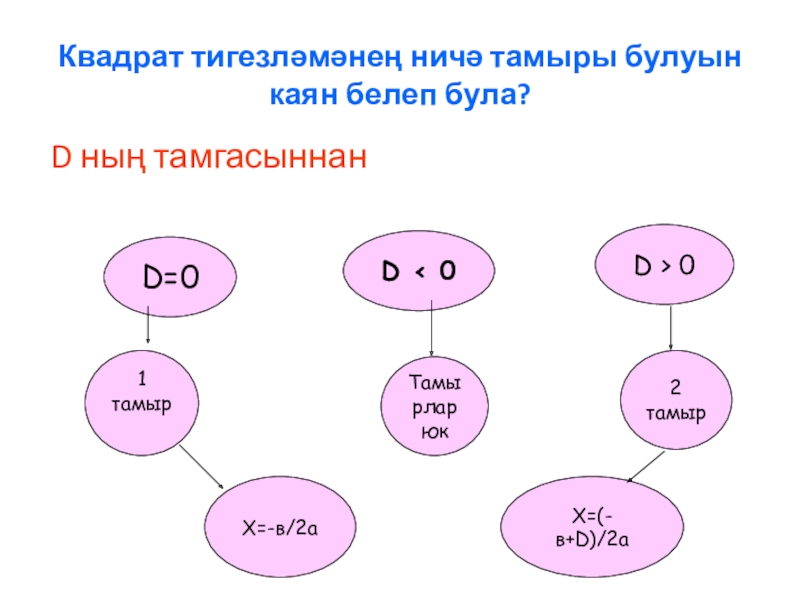
- 10. Квадрат тигезләмәнең ничә тамыры булуын каян белеп була? D ның тамгасыннан
- 11. Формула кулланып тигезләмәне чиш: 1 вариант
- 12. Виет теоремасыКитерелгән квадрат тигезләмәнең тамырлары суммасы
- 13. X1 = 4 и X2 =10Z1=-10
- 14. Физкультминутка
Слайд 2
рәвешендәге тигезләмә квадрат тигезләмә дип атала, биредә х-үзгәрешле, a,b һәм с
Билгеләмә
Слайд 3а) 6х2 – х + 4 = 0
б) 12х - х2
в) 8 + 5х2 = 0
г) х – 6х2 = 0
д) - х + х2 = 15
Квадрат тигезләмәнең коэффиентларын ачыклагыз:
а = -1, в = 12, с = 7;
а = -6, в = 1, с = 0;
а = 6, в = -1, с = 4.
а = 5, в = 0, с = 8;.
а = 1, в =-1, с = -15.
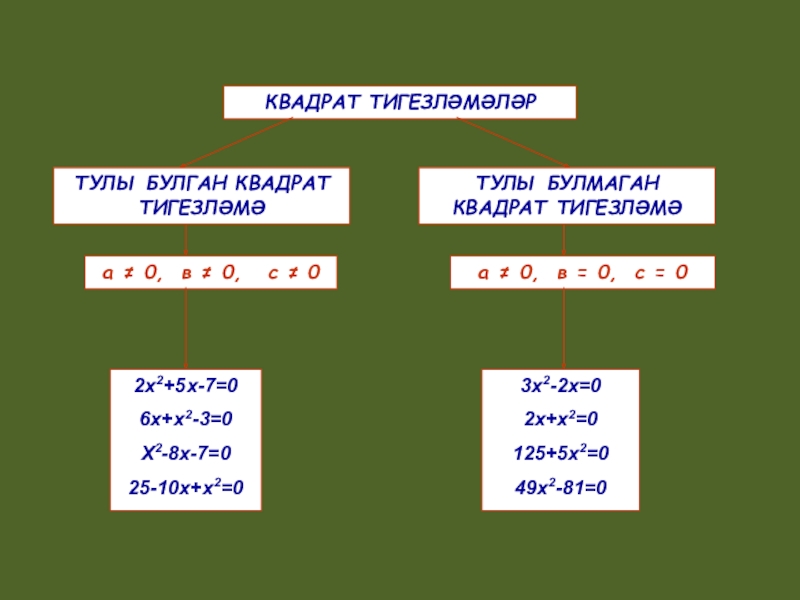
Слайд 4ТУЛЫ БУЛГАН КВАДРАТ ТИГЕЗЛӘМӘ
ТУЛЫ БУЛМАГАН КВАДРАТ ТИГЕЗЛӘМӘ
КВАДРАТ ТИГЕЗЛӘМӘЛӘР
а ≠ 0, в
а ≠ 0, в = 0, с = 0
2х2+5х-7=0
6х+х2-3=0
Х2-8х-7=0
25-10х+х2=0
3х2-2х=0
2х+х2=0
125+5х2=0
49х2-81=0
Слайд 5
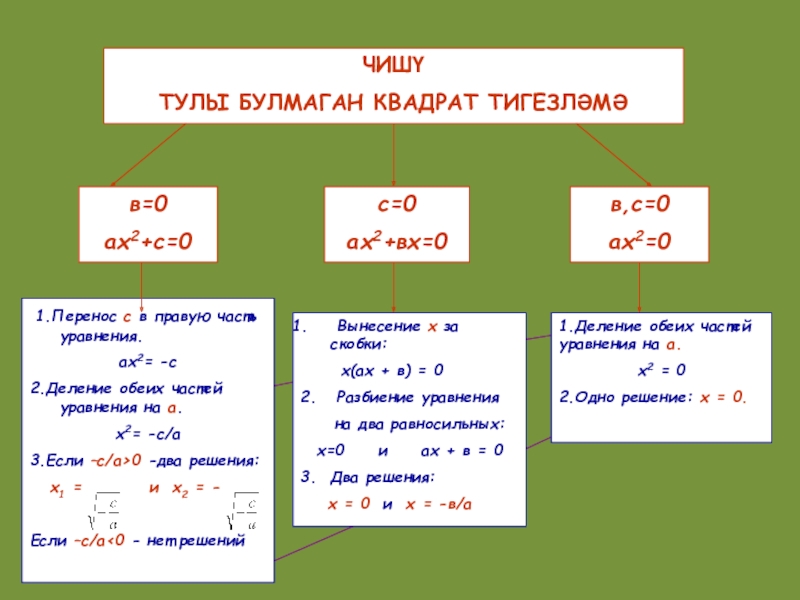
ЧИШҮ
ТУЛЫ БУЛМАГАН КВАДРАТ ТИГЕЗЛӘМӘ
в=0
ах2+с=0
с=0
ах2+вх=0
в,с=0
ах2=0
1.Перенос с в правую часть уравнения.
ах2= -с
2.Деление
х2= -с/а
3.Если –с/а>0 -два решения:
х1 = и х2 = -
Если –с/а<0 - нет решений
Вынесение х за скобки:
х(ах + в) = 0
2. Разбиение уравнения
на два равносильных:
х=0 и ах + в = 0
3. Два решения:
х = 0 и х = -в/а
1.Деление обеих частей уравнения на а.
х2 = 0
2.Одно решение: х = 0.
Слайд 6
МӨСТӘКЫЙЛЬ ЭШЛӘ :
1 вариант:
а) 2х + х2= 0
б) 49х2 – 81 = 0
2 вариант:
а) 3х2 – 2х = 0
б) 125 + 5х2 = 0
Слайд 7ҖАВАПЛАР
1 вариант:
а) 2х + х2= 0 ;
Х(2+х)=0;
Х=0 яки 2+х=0;
Җавап:
б) 49х2 – 81 = 0
Җавап:
2 вариант:
а) 3х2-2х= 0 ;
Х(3х-2)=0;
Х=0 яки 3х-2=0;
3х=2
Җавап:
б) 125 + 5х2 = 0
Җавап: тигезләмәнең чишелеше юк
Слайд 8
Тулы булган квадрат тигезләмәләрне чишү ысуллары
Ике буынның квадратын аерып чыгару юлы
2.Формула:
Икенче коэффиценты җөп сан булганда
Формула: D= b2- ac, x1,2=
3. Виета теоремасы.
Слайд 9Тигезләмәне чишегез:
Икебуыннын квадратын аерып чыгару юлы белән
1 вариант: х2 -6х -7 = 0
2 вариант: х2 – 8х -9 = 0
Слайд 11
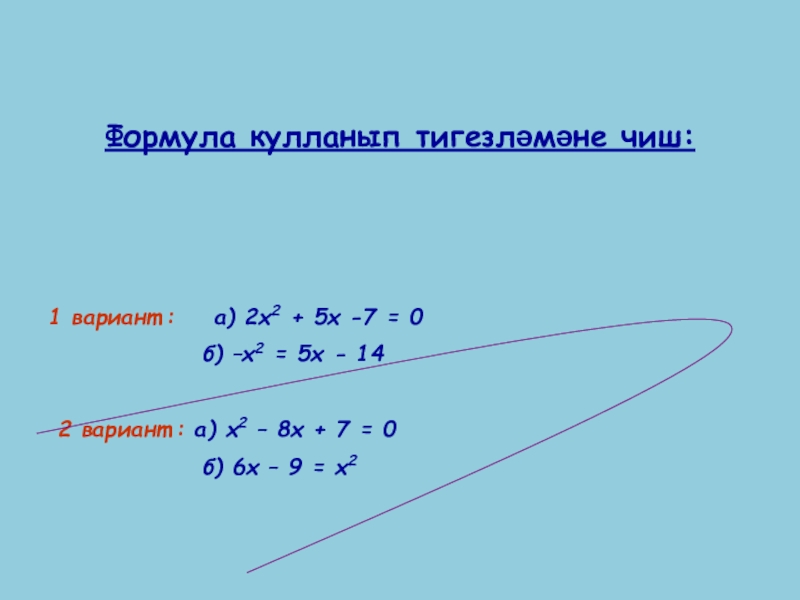
Формула кулланып тигезләмәне чиш:
1 вариант : а) 2х2
б) –х2 = 5х - 14
2 вариант : а) х2 – 8х + 7 = 0
б) 6х – 9 = х2
Слайд 12 Виет теоремасы
Китерелгән квадрат тигезләмәнең тамырлары суммасы капма-каршы тамгасы белән алынган
х2+px+g=0- китерелгән квадрат тигезләмә
Виет теоремасы буенча:
х1 + х2= -p
х1* х2= g