- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Геометрическая интерпретация при решении уравнений, содержащих знак модуля
Содержание
- 1. Презентация по математике на тему Геометрическая интерпретация при решении уравнений, содержащих знак модуля
- 2. Геометрическая интерпретация при решении уравнений, содержащих знак модуля
- 3. Повторим определение модуля.Продолжите фразу:Модулем положительного числа…Модулем отрицательного числа… Модулем нуля…
- 4. Повторим определение модуля.Продолжите фразу:Модулем числа а называют
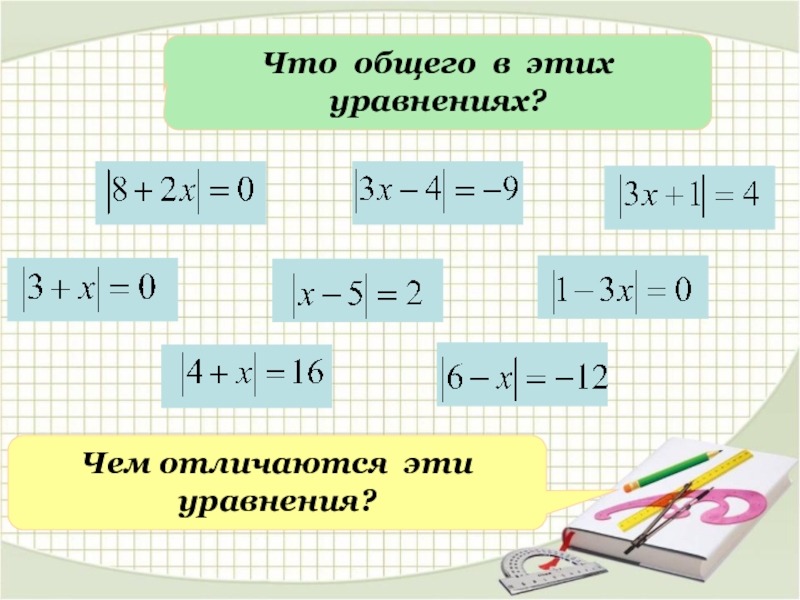
- 5. Что общего в этих уравнениях?Чем отличаются эти уравнения?
- 6. Разделите уравнения на группы.По какому принципу можно разделить уравнения?
- 7. Решим уравнениеОтвет: -1; 13.1. Найдем значение, при
- 8. Решим уравнение-31-7+4-4Следовательно, 2х = -7 или
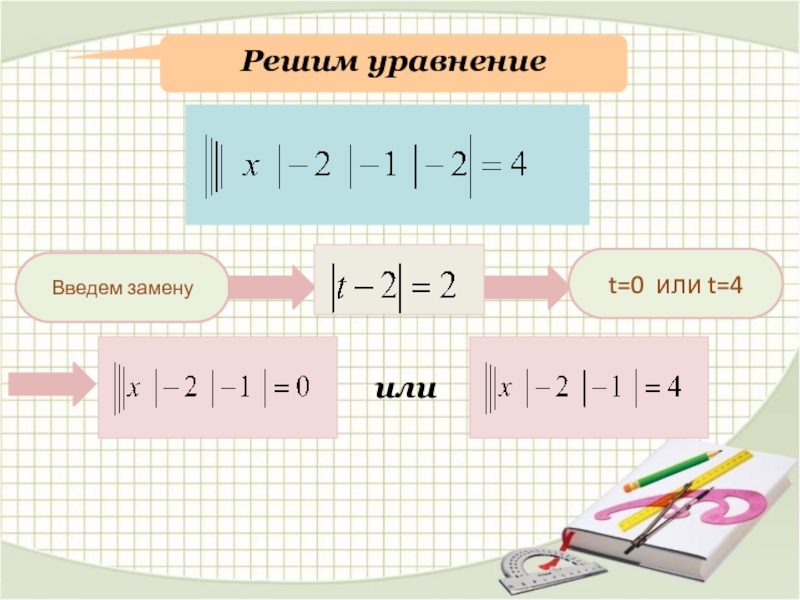
- 9. Решим уравнениеВведем заменуt=0 или t=4или
- 10. Решим уравнениеили
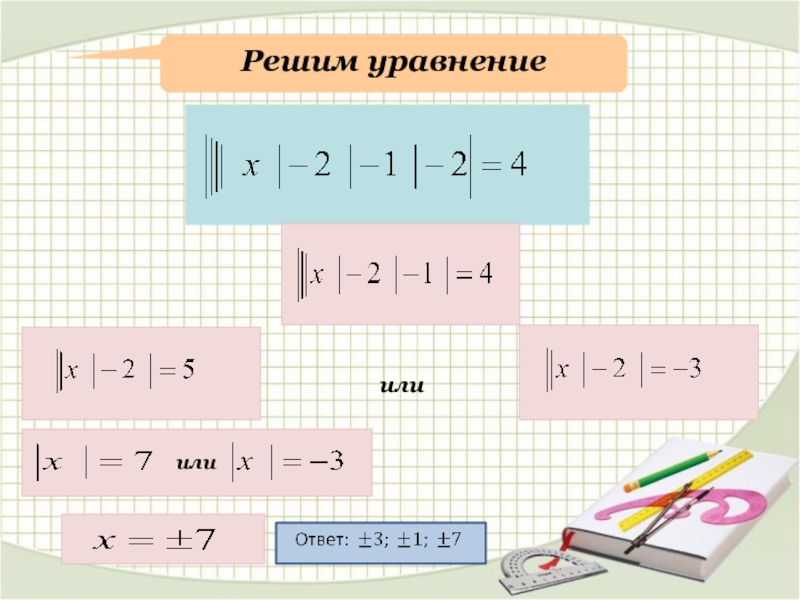
- 11. Решим уравнениеилиили
- 12.
- 13. | х-3 | + | х-1 |
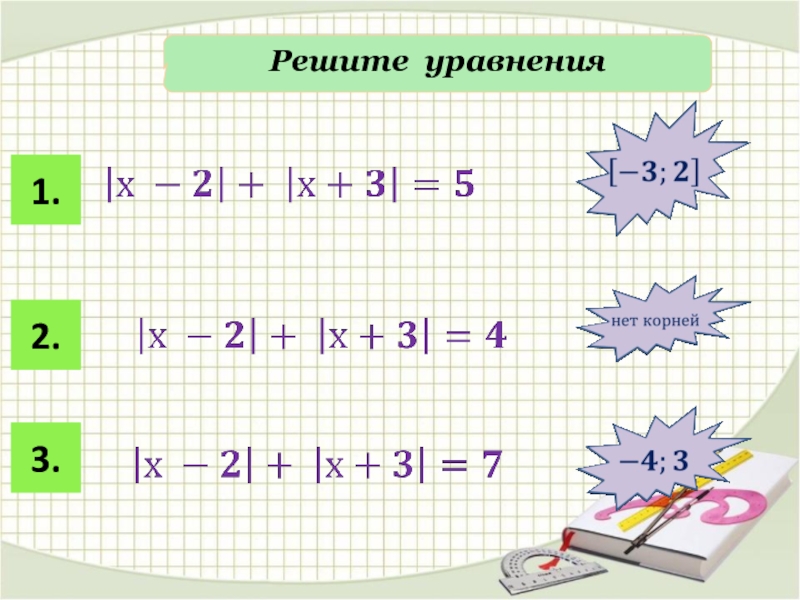
- 14. Решите уравнения1.2.3.
- 15. ВыводСколько решений может иметь уравнение | х-a |+ | х-d | = c?
- 16. ПодумайтеПри каких значениях а уравнение имеет только два корня?
- 17. | х-5 | - | х-2 |
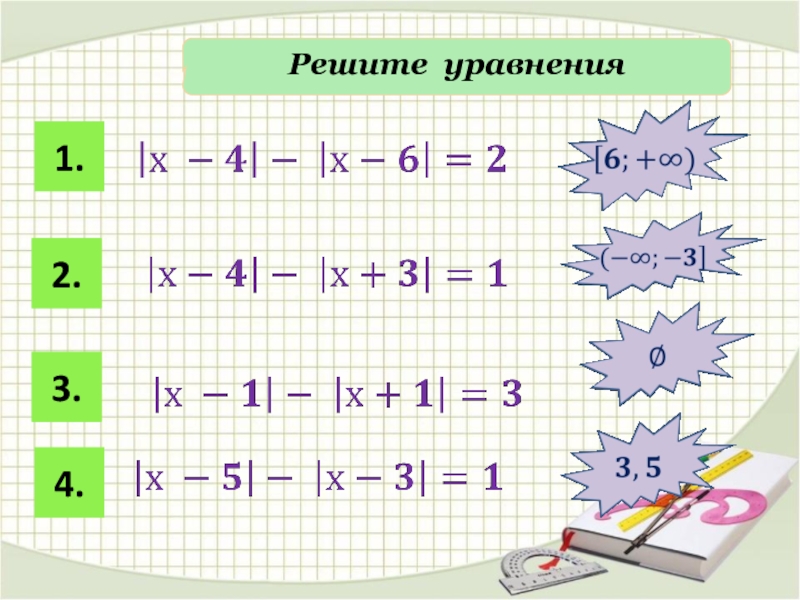
- 18. Решите уравнения1.2.3.4.
- 19. ВыводСколько решений может иметь уравнение | х-a |- | х-d | = c?
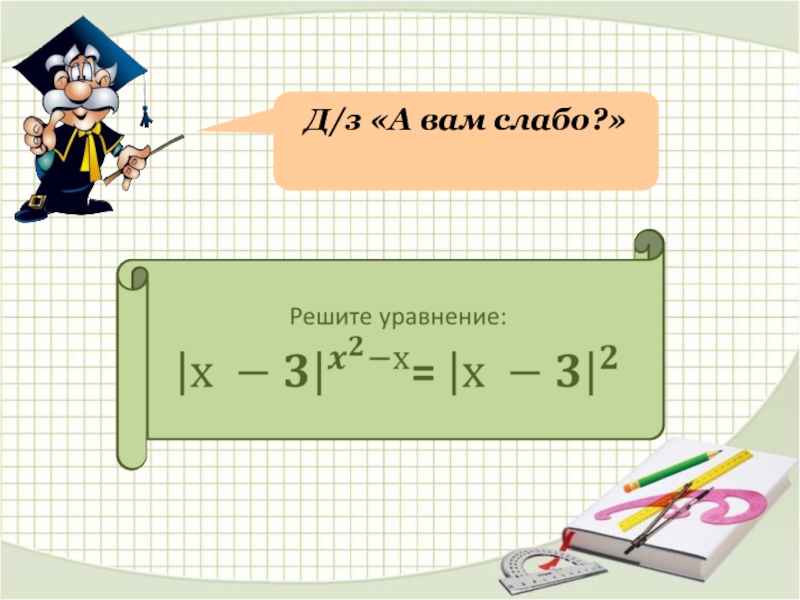
- 20. Д/з «А вам слабо?»
- 21. Слайд 21
Геометрическая интерпретация при решении уравнений, содержащих знак модуля
Слайд 1Презентацию подготовила учитель математики МБОУ «Октябрьская школа-гимназия»
Сапунцова Наталья Юрьевна
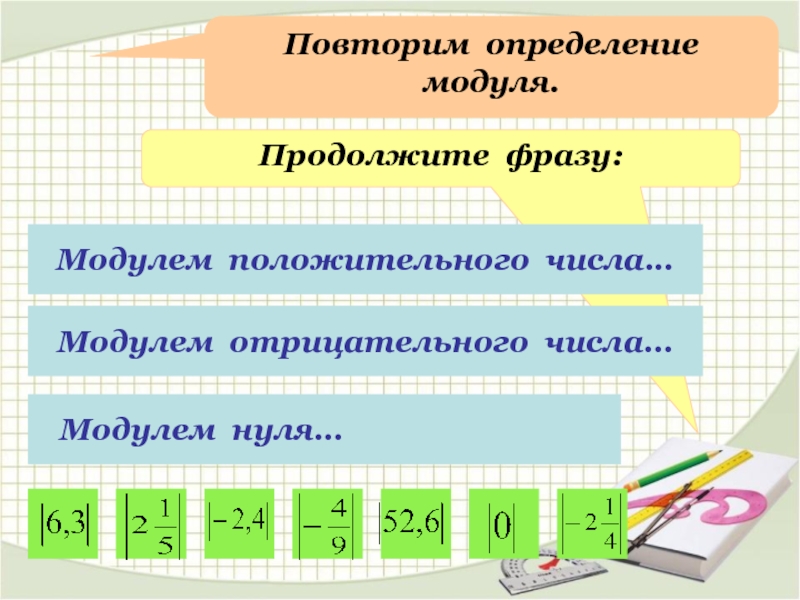
Слайд 3Повторим определение модуля.
Продолжите фразу:
Модулем положительного числа…
Модулем отрицательного числа…
Модулем нуля…
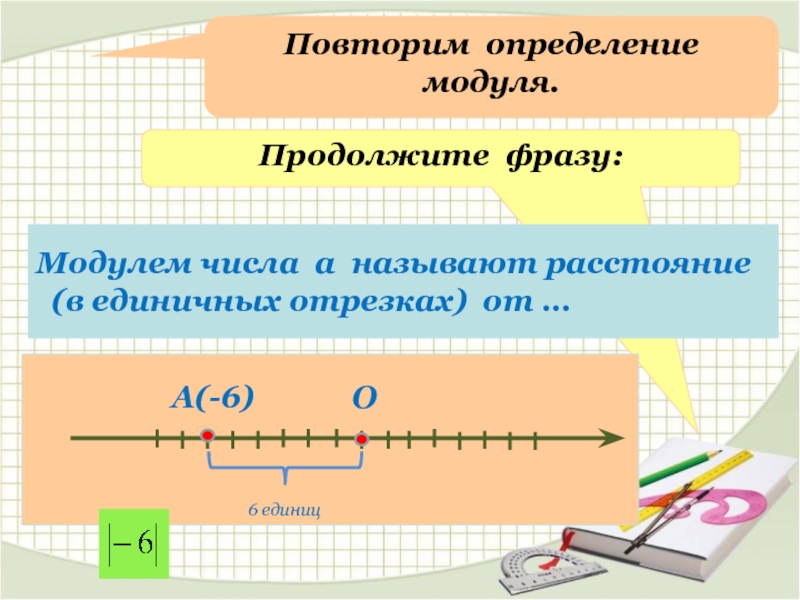
Слайд 4Повторим определение модуля.
Продолжите фразу:
Модулем числа а называют расстояние
(в единичных отрезках)
от …
О
А(-6)
6 единиц
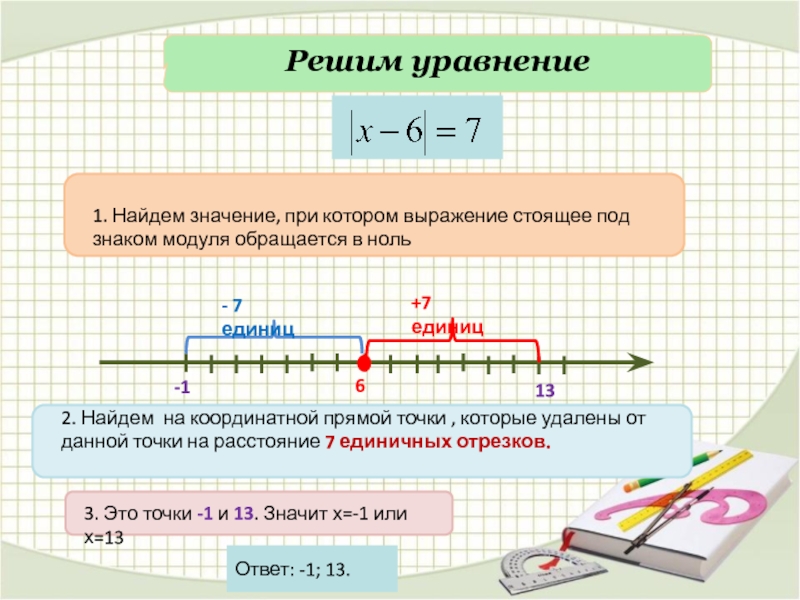
Слайд 7Решим уравнение
Ответ: -1; 13.
1. Найдем значение, при котором выражение стоящее под
знаком модуля обращается в ноль
2. Найдем на координатной прямой точки , которые удалены от данной точки на расстояние 7 единичных отрезков.
6
+7 единиц
- 7 единиц
3. Это точки -1 и 13. Значит х=-1 или х=13
13
-1
Слайд 12
Ответ:
а) Если а=0, то уравнение имеет одно решение;
б) Если а>0, то уравнение имеет 2 корня,
в) Если а<0, то уравнение не имеет корней
а) Если а=0, то уравнение имеет одно решение;
б) Если а>0, то уравнение имеет 2 корня,
в) Если а<0, то уравнение не имеет корней
Вывод
Сколько решений может иметь уравнение | х-b | = а,
в зависимости от значений а?
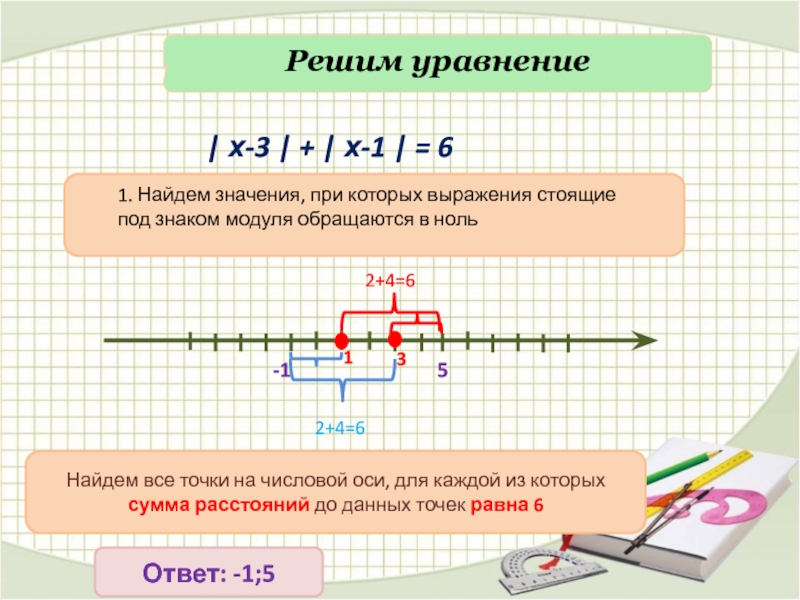
Слайд 13| х-3 | + | х-1 | = 6
Решим уравнение
1. Найдем
значения, при которых выражения стоящие под знаком модуля обращаются в ноль
Найдем все точки на числовой оси, для каждой из которых сумма расстояний до данных точек равна 6
2+4=6
2+4=6
1
3
5
-1
Ответ: -1;5
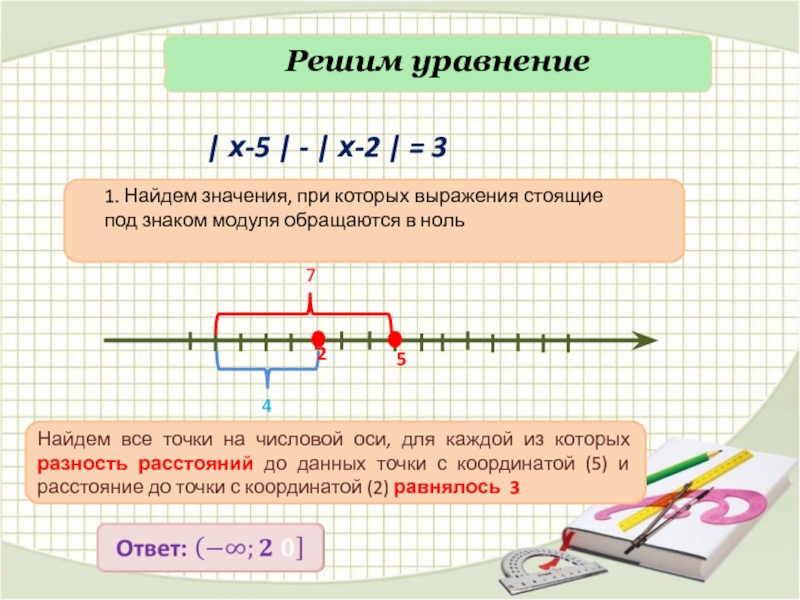
Слайд 17| х-5 | - | х-2 | = 3
Решим уравнение
1. Найдем
значения, при которых выражения стоящие под знаком модуля обращаются в ноль
Найдем все точки на числовой оси, для каждой из которых разность расстояний до данных точки с координатой (5) и расстояние до точки с координатой (2) равнялось 3
7
4
2
5
