Презентация, доклад по математике на тему: Формирование общего способа решения в классе иррациональных уравнений

внешнеречевом
внутреннем

Решение иррационального уравнения стандартного вида

Цель

Характеристика 2. Теорема 3. Переход 4. Задача
5. Уравнение 6.Способ 7.Решение 8.Неравенство
9.Отбор 10.Решение 11.Переход 12.Анализ
13.Оценка

О.

К.

Ц.

О.

К.

3 4 5 6 7 8 9 10 11 12 13


1. (Характеристика) рациональность выражений; сведение к рациональному уравнению.
2. (Теорема) равносильность исходного уравнения и системы.
3. (Переход) применение теоремы для конкретного уравнения.
4. (Задача) постановка задачи решения системы.
5. (Уравнение) постановка задачи решения уравнения системы.
6. (Способ) общий способ решения рационального уравнения.
7. (Решение) решение рационального уравнения.
8. (Неравенство) задача отбора корней рационального уравнения.
9. (Отбор) отбор корней уравнения, удовлетворяющих неравенству системы.
10. (Система) характеристика решений системы.
11.(Решения) характеристика решений исходного уравнения.
12.(Анализ) анализ процесса решения для установления способа.
13.(Оценка) оценка общности выделенного способа.

вида I.
2. Теорема о равносильном переходе к системе.
3. Равносильный переход к системе.
4. Постановка задачи решения системы.
5. Постановка задачи решения рационального уравнения системы.
6. Общий способ решения рационального уравнения.
7. Решение уравнения стандартного вида общим способом.
8. Постановка задачи отбора решений, удовлетворяющих неравенству.
9. Отбор решений.
10. Анализ решений системы.
11. Характеристика решений исходного уравнения.
12. Анализ решения иррационального уравнения вида I.
13. Оценка общности действий в классе уравнений вида I.

уравнений вида


1 2 3 4 5 6 7 8 9 10 11 12 13


К. Действия в конкретном уравнении


8. О. Исследовать задачу выделения множества решений рационального уравнения , которые содержатся во множестве
К. Исследуем задачу выделения множества решений рационального уравнения , которые содержатся во множестве

конкретном уравнении


О. Действия в классе уравнений

4

5

6

7

8

9

10

11

12

13

1

2

3

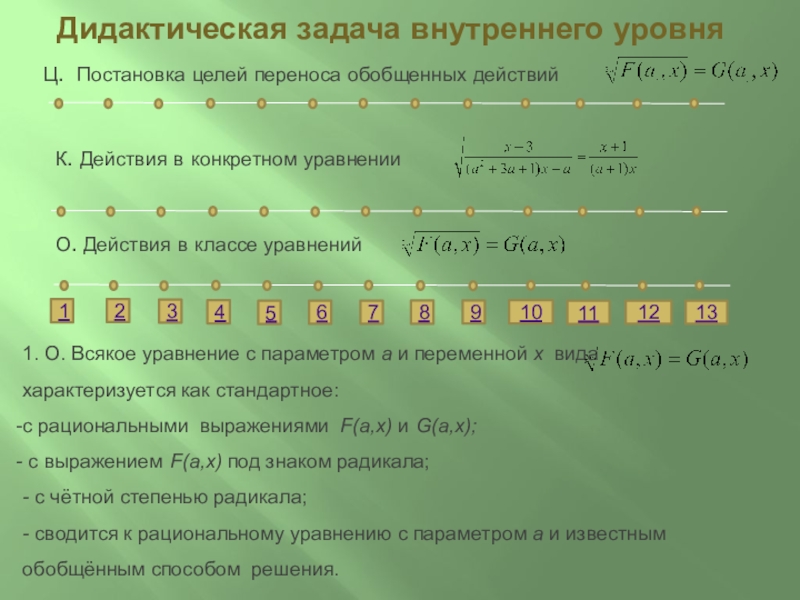
1. О. Всякое уравнение с параметром а и переменной x вида характеризуется как стандартное:
с рациональными выражениями F(a,x) и G(a,x);
с выражением F(a,x) под знаком радикала;
- с чётной степенью радикала;
- сводится к рациональному уравнению с параметром а и известным обобщённым способом решения.

конкретном уравнении


О. Действия в классе уравнений

4

5

6

7

8

9

10

11

12

13

1

2

3

2. О. Для каждого допустимого значения параметра а иррациональное уравнение вида равносильно системе ,

то есть уравнению на множестве .

конкретном уравнении


О. Действия в классе уравнений

4

5

6

7

8

9

10

11

12

13

1

2

3

3. О. Исследование всякого иррационального уравнения стандартного вида
с параметром а, переменной х и чётной степенью радикала в соответствии с теоремой (1) сводится к исследованию рационального уравнения на множестве .

конкретном уравнении


О. Действия в классе уравнений

4

5

6

7

8

9

10

11

12

13

1

2

3

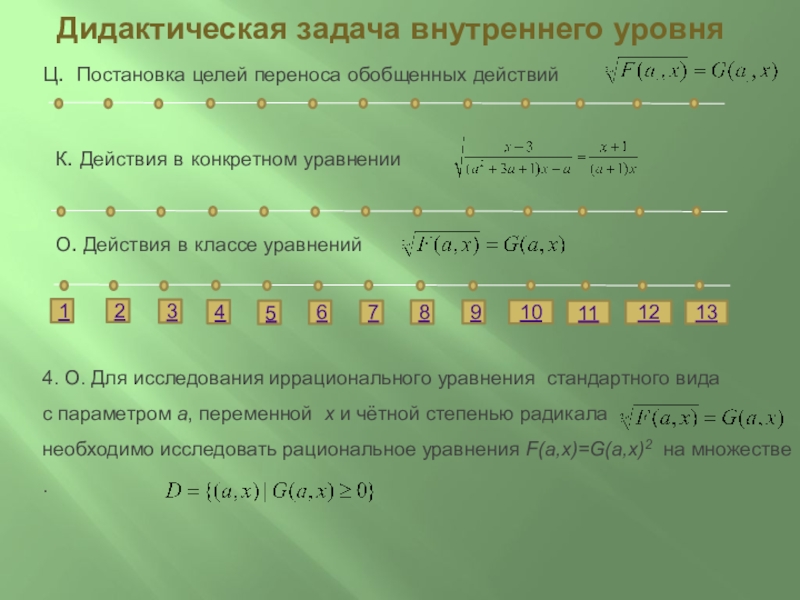
4. О. Для исследования иррационального уравнения стандартного вида
с параметром а, переменной х и чётной степенью радикала необходимо исследовать рациональное уравнения F(a,x)=G(a,x)2 на множестве .

конкретном уравнении


О. Действия в классе уравнений

4

5

6

7

8

9

10

11

12

13

1

2

3

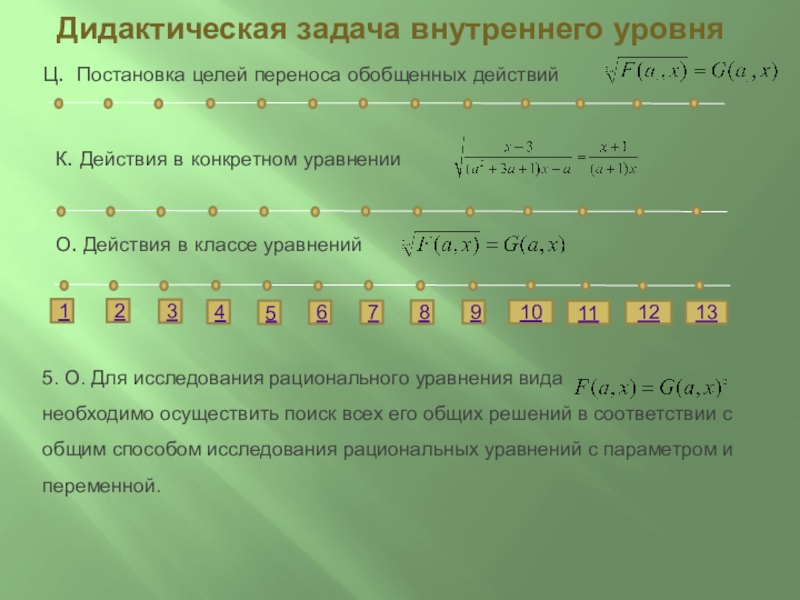
5. О. Для исследования рационального уравнения вида необходимо осуществить поиск всех его общих решений в соответствии с общим способом исследования рациональных уравнений с параметром и переменной.

конкретном уравнении


О. Действия в классе уравнений

4

5

6

7

8

9

10

11

12

13

1

2

3

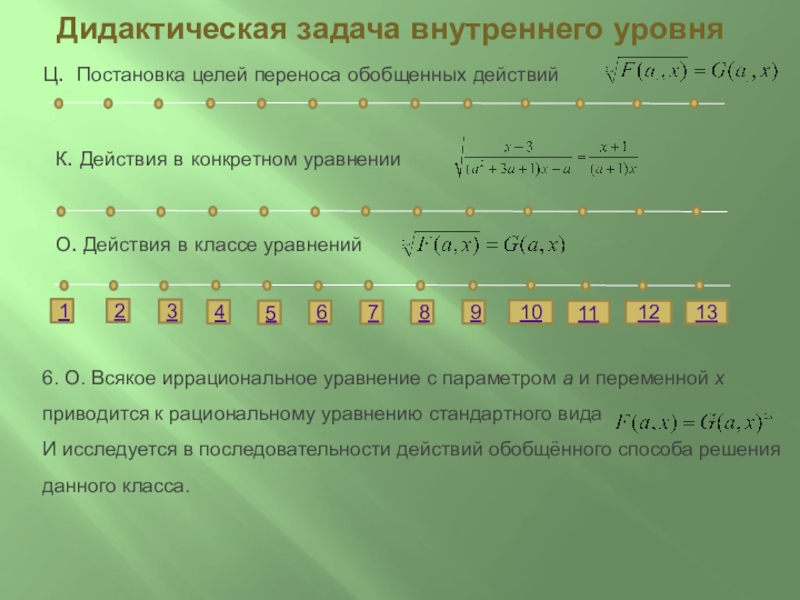
6. О. Всякое иррациональное уравнение с параметром а и переменной x приводится к рациональному уравнению стандартного вида
И исследуется в последовательности действий обобщённого способа решения данного класса.

конкретном уравнении


О. Действия в классе уравнений

4

5

6

7

8

9

10

11

12

13

1

2

3

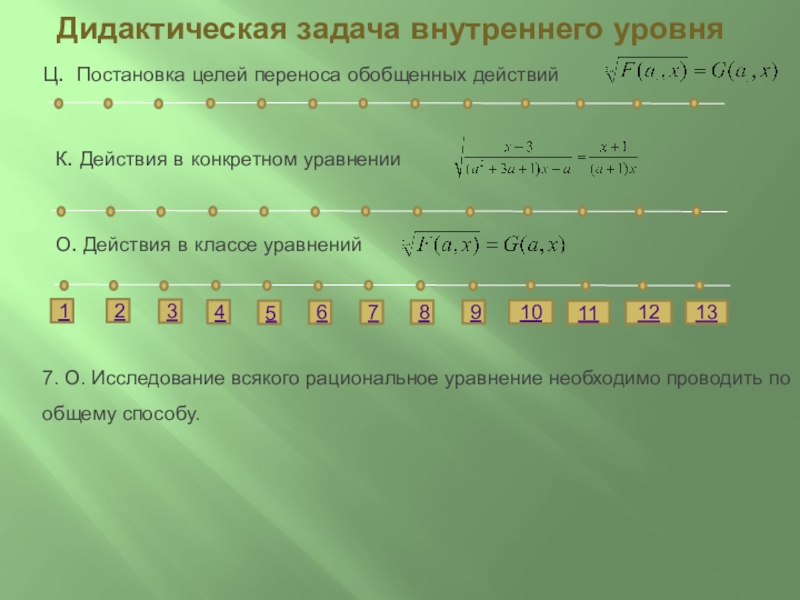
7. О. Исследование всякого рациональное уравнение необходимо проводить по общему способу.

конкретном уравнении


О. Действия в классе уравнений

4

5

6

7

8

9

10

11

12

13

1

2

3

8. О. Всякое рациональное уравнение с параметром а и переменной x сводится к стандартному виду , из числителя
которого находятся все КЗП и все общие решения.
Из выражений H(a,x)=0 и M(a,x)=0 находятся ограничения на соответствующие области значений параметра.
Для КЗП находятся частные решения соответствующих уравнений.

конкретном уравнении


О. Действия в классе уравнений

4

5

6

7

8

9

10

11

12

13

1

2

3

9. О. Для фиксации общих решений иррационального уравнения вида
необходимо осуществить отбор общих решений рационального уравнения на множестве

конкретном уравнении


О. Действия в классе уравнений

4

5

6

7

8

9

10

11

12

13

1

2

3

10. О. Для фиксации общих решений иррационального уравнения вида
необходимо осуществить отбор общих решений рационального уравнения , зафиксированных на множествах
, , ,удовлетворяющих неравенству .

конкретном уравнении


О. Действия в классе уравнений

4

5

6

7

8

9

10

11

12

13

1

2

3

10. О. Для всякого иррационального уравнения общие решения имеют вид на множестве , где х= - общее решение рационального уравнения на множестве значений параметра, множество значений параметра состоит из тех значений , для которых .

конкретном уравнении


О. Действия в классе уравнений

4

5

6

7

8

9

10

11

12

13

1

2

3

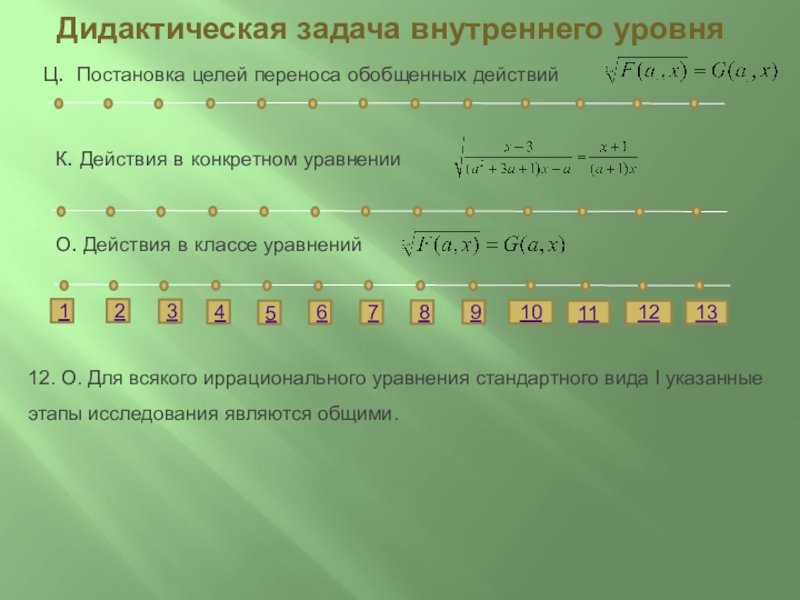
12. О. Для всякого иррационального уравнения стандартного вида I указанные этапы исследования являются общими.

конкретном уравнении


О. Действия в классе уравнений

4

5

6

7

8

9

10

11

12

13

1

2

3

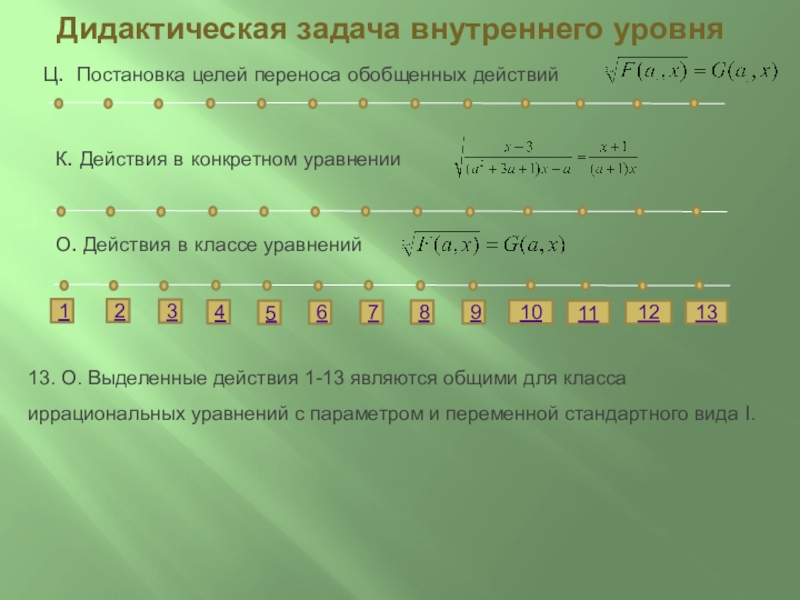
13. О. Выделенные действия 1-13 являются общими для класса иррациональных уравнений с параметром и переменной стандартного вида I.

операционный состав в системе дидактических задач;
не обеспечен процесс формирования общего способа действия в классе уравнений.

2. В деятельностной теории учения по исследованию иррациональных уравнений:
действие формируется на всех уровнях в едином операционном составе;
действие обобщается на класс, совокупность классов.

полный операционный состав закономерного плана;
б) установлен общий способ решения в классе всех систем иррациональных уравнений стандартного вида I, II и III;
в) установлен общий способ решения в классе всех иррациональных неравенств с параметром стандартного вида.

системы средствами мультимедиа
создать методическую систему, позволяющую создавать системы данного класса
рассмотрение других классов систем (логарифмических, тригонометрических, показательных)