- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Элементы теории тригонометрических функций (10 класс)
Содержание
- 1. Презентация по математике на тему Элементы теории тригонометрических функций (10 класс)
- 2. Числовая окружность на координатной плоскости
- 3. Числовая окружность на координатной плоскости Для
- 4. Числовая окружность на координатной плоскости
- 5. Числовая окружность на координатной плоскости Найдем
- 6. Числовая окружность на координатной плоскости В
- 7. Использованные ресурсыАлгебра и начала анализа. 10 класс. В 2 ч. Ч.1. Учебник (профильный уровень) Мордкович А.Г., Семенов П.В.,2007
Числовая окружность на координатной плоскости Расположим числовую окружность в декартовой прямоугольной системе координат: центр окружности совместим с началом координат, ее радиус примем за масштабный отрезок.А = А(1;0), В = В(0;1), С = С(-1;0), D
Слайд 1Элементы теории тригонометрических
функций
Выполнила учитель математики
МОУ лицей №86
Корнева
Елена Владимировна
г.Ярославль
2008
Слайд 2Числовая окружность на координатной плоскости
Расположим числовую окружность
в декартовой прямоугольной системе координат: центр окружности совместим с началом координат, ее радиус примем за масштабный отрезок.
А = А(1;0), В = В(0;1),
С = С(-1;0), D = D(0;-1)
Слайд 3Числовая окружность на координатной плоскости
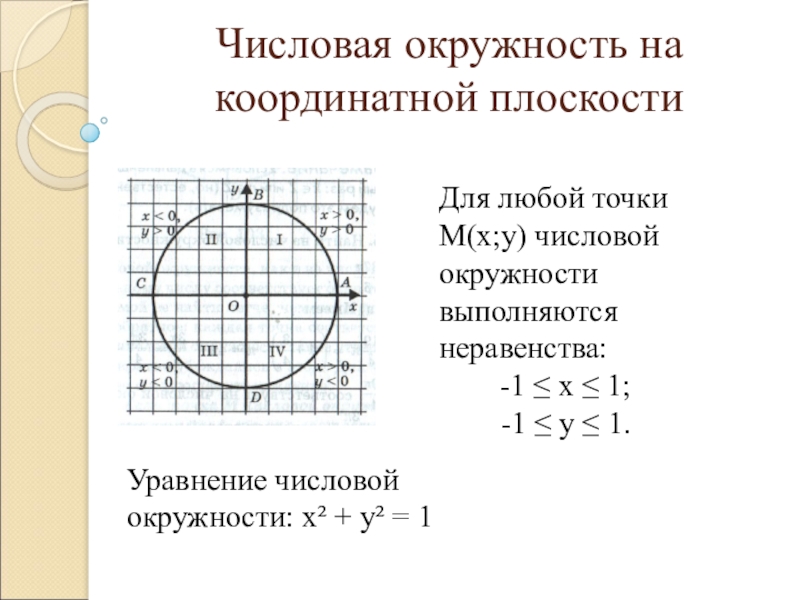
Для любой точки М(х;у) числовой
окружности выполняются неравенства:
-1 ≤ х ≤ 1;
-1 ≤ у ≤ 1.
-1 ≤ х ≤ 1;
-1 ≤ у ≤ 1.
Уравнение числовой окружности: х² + у² = 1
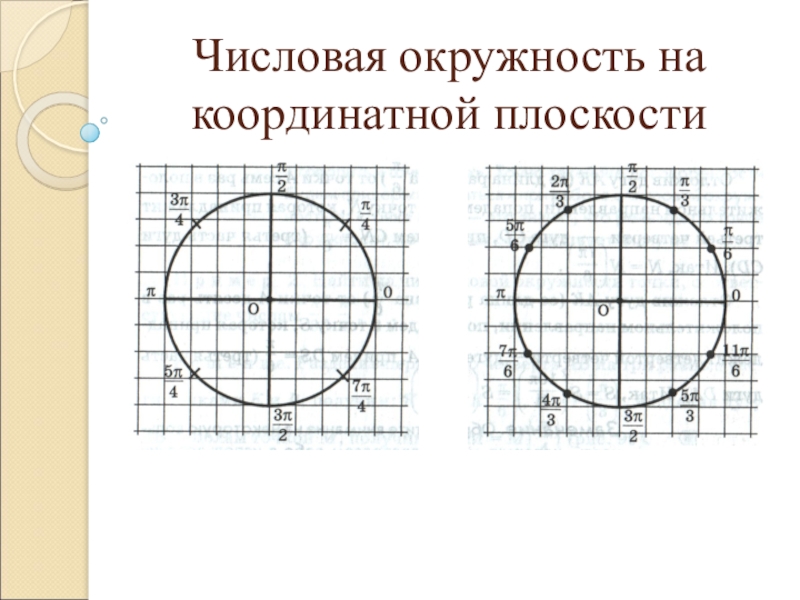
Слайд 5Числовая окружность на координатной плоскости
Найдем координаты точки М –
середины первой координатной четверти.
М(х;у), причем, х = у.
Координаты точки удовлетворяют уравнению окружности
х² + у² = 1
Точке М на числовой окружности соответствует число
π ∕4
Слайд 6Числовая окружность на координатной плоскости
В результате, чтобы найти координаты
точки М необходимо решить систему уравнений
при условии, х > 0, у > 0.
Решением является пара чисел .
при условии, х > 0, у > 0.
Решением является пара чисел .
Слайд 7Использованные ресурсы
Алгебра и начала анализа. 10 класс. В 2 ч. Ч.1.
Учебник (профильный уровень) Мордкович А.Г., Семенов П.В.,2007