- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Элементы комбинаторики
Содержание
- 1. Презентация по математике на тему Элементы комбинаторики
- 2. Основные понятия:КомбинаторикаПравило сложенияПравило умножения Факториал ПерестановкиПерестановки с
- 3. Комбинаторика.«комбинаторика» происходит от латинского слова combinare –
- 4. Как всё начиналось…Термин «комбинаторика» был введён в
- 5. Основы комбинаторики и теории вероятностей создали и
- 6. После появления математического анализа обнаружилась тесная связь комбинаторных и
- 7. Комбинаторика и ее применение в реальной жизни.Замечательно,
- 8. Области применения комбинаторики:лингвистика (рассмотрение вариантов комбинаций букв).учебные заведения (составление расписаний);сфера общественного питания (составление меню);
- 9. производство (распределение нескольких видов работ между рабочими);география (раскраска карт);спортивные соревнования (расчёт количества игр между участниками);
- 10. химия (анализ возможных связей между химическими элементами);агротехника (размещение посевов на нескольких полях);азартные игры (подсчёт частоты выигрышей);
- 11. астрология (анализ расположения планет и созвездий);биология (расшифровка кода ДНК);военное дело (расположение подразделений);
- 12. доставка почты (рассмотрение вариантов пересылки).экономика (анализ вариантов купли-продажи акций);криптография (разработка методов шифрования);
- 13. Правило сложения:Если некоторый объект А можно выбрать
- 14. Задача:Сколько двузначных чисел можно составить из цифр
- 15. Задача:2 способ: дерево возможных вариантов. Для этой
- 16. Правило умножения: Если объект А можно выбрать m способами и
- 17. Задача 1 Сколько различных двузначных чисел
- 18. Упражнения:№ 1043Сколько различных двузначных чисел с разными
- 19. № 1045Сколько различных трехзначных чисел, не имеющих
- 20. № 147Путешественник может попасть из пункта А
- 21. № 1048Чтобы попасть из города М в
- 22. № 1049№ 1050№ 10521) 992
- 23. № 1053№ 1054№1055В классе 18 учащихся. Из
- 24. Факториал.Таблица факториалов:Определение. Факториалом натурального числа n называется
- 25. № 1064Упростить формулу записи выражений (полагая, что k-натуральное число, k>4) 1)3) 5)
- 26. Слайд 26
- 27. Упростить формулу записи выражений (полагая, что k-натуральное
- 28. ПерестановкиСочетанияи их свойстваРазмещения
- 29. Перестановки
- 30. Перестановками из n элементов называются соединения (комбинации),
- 31. Число перестановок:(1)Произведение первых n натуральных чисел обозначают
- 32. № 1059 Найти значение:
- 33. Пример 1. Сколькими способами могут быть расставлены
- 34. Пример 3. Имеется 10 различных книг, среди
- 35. Перестановки с повторениями.Определение .Число перестановок n –
- 36. Размещения
- 37. Задача 1.Сколько различных двузначных чисел можно записать
- 38. Размещениями из m элементов по n элементов
- 39. = m(m – 1)(m – 2) •
- 40. Вычислить:Задача 5Ответ: 225Упражнения:№ 1073 – № 1075
- 41. Задача 5. Из 12 учащихся нужно отобрать
- 42. Задача 6. Сколько существует семизначных телефонных номеров,
- 43. Размещения с повторениями.Определение.k – размещением с повторениями
- 44. Сочетание и их свойства
- 45. Определение. Подмножества, составленные из n элементов данного
- 46. Равенство:Число размещений, перестановок и сочетаний связаны равенством:
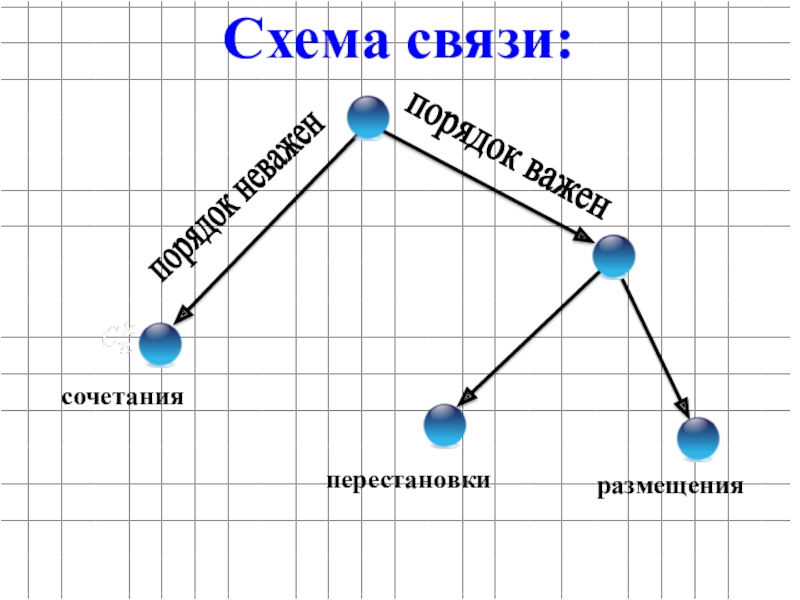
- 47. порядок важенпорядок неваженсочетания перестановки размещения Схема связи:
- 48. Учимся различать виды соединений.Pn
- 49. Пример 1. Сколькими способами можно выбрать трёх дежурных из класса, в котором 20 человек?Решение:
- 50. Пример 2. Из вазы с цветами, в
- 51. Пример 3. Семь огурцов и три помидора
- 52. «Би»-удвоение, раздвоение …«Ном»(фран. nombre) –номер, нумерация.«Бином» -»два
- 53. 2) Число всех членов разложения на единицу
- 54. 5) Сумма биномиальных коэффициентов всех членов разложения
- 55. 8)Любой биномиальный коэффициент, начиная со второго, равен
- 56. Пример . Доказать, что при любом натуральном
- 57. 1 1 1
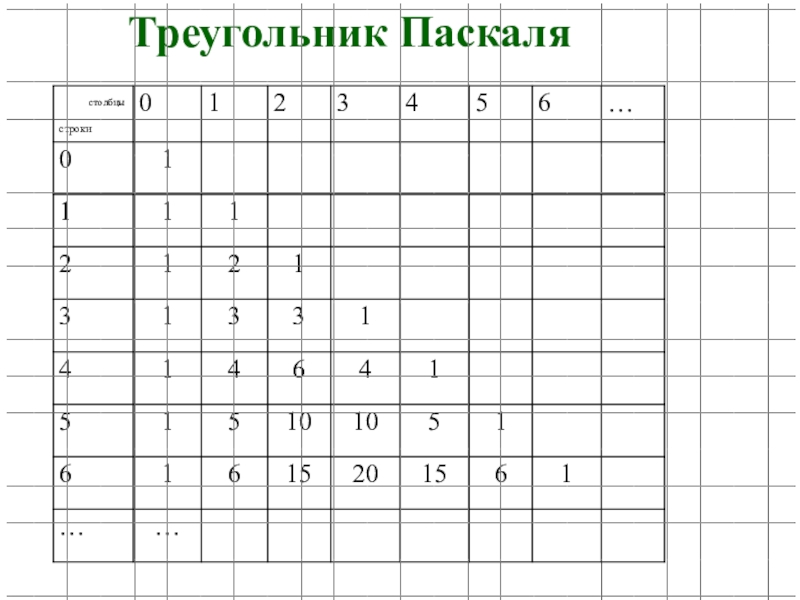
- 58. Треугольник Паскаля
- 59. …Треугольник Паскаля
- 60. Различие между перестановками, размещениями, сочетаниямиВ случае перестановок
- 61. Проверь себя Что такое комбинаторика?В чём состоит
- 62. О пользе комбинаторики или лишних знаний не бывает
- 63. 1.2.отгадай ребусы
- 64. 3.4.5.отгадай ребусы
- 65. Ответы:ВариантСочетанияФакториалСобытиеИсход
- 66. Спасибо за внимание!
- 67. Д/З: § 60, №№ 1051, 1055. Д/З:
- 68. Электронные ресурсы: кубики: http://free-math.ru/load/prezentacii_egeh_po_matematike/verojatnost_i_kombinatornoe/38-1-0-173 лилии:http://ru.gde-fon.com/cvety?offset[0]=648http://ru.gde-fon.com/cvety?offset[0]=666http://ru.gde-fon.com/cvety?offset[0]=4590шаблон:http://www.myshared.ru/slide/56405/Санкт-Петербург, 2014
Слайд 1Элементы
комбинаторики
Преподаватель: Перминова Е.В.
ГБПОУ СО «Свердловский педагогический коллеж»
Слайд 2Основные понятия:
Комбинаторика
Правило сложения
Правило умножения
Факториал
Перестановки
Перестановки с повторениями
Размещения
Размещения с повторениями
Равенство
Схема связи между размещениями, перестановками и сочетаниями
Учимся различать виды соединений
Бином Ньютона и его свойства
Треугольник Паскаля
Различие между перестановками, размещениями, сочетаниями
Проверь себя
Слайд 3Комбинаторика.
«комбинаторика» происходит от латинского слова combinare – «соединять, сочетать».
Определение. Комбинаторика –
Слайд 4Как всё начиналось…
Термин «комбинаторика» был введён в математический обиход Лейбницем, который
Первоначально комбинаторика возникла в XVI в. в связи с распространением различных азартных игр.
известный немецкий учёный Готфрид Вильгельм Лейбниц.
(1.07.1646 - 14.11.1716)
Слайд 5Основы комбинаторики и теории вероятностей создали и разработали французские математики XVII
Пьер Ферма (1601-1665)
Блез Паскаль (1623-1662)
Слайд 6После появления математического анализа обнаружилась тесная связь комбинаторных и ряда аналитических задач. Абрахам де
Абрахам де Муавр, английский математик (1667-1754)
Джеймс Стирлинг, шотландский математик (1692-1770)
Слайд 7Комбинаторика и ее применение в реальной жизни.
Замечательно, что наука, которая начала
П. Лаплас
Слайд 8Области применения комбинаторики:
лингвистика (рассмотрение вариантов комбинаций букв).
учебные заведения (составление расписаний);
сфера общественного
Слайд 9производство (распределение нескольких видов работ между рабочими);
география (раскраска карт);
спортивные соревнования (расчёт
Слайд 10химия (анализ возможных связей между химическими элементами);
агротехника (размещение посевов на нескольких
азартные игры (подсчёт частоты выигрышей);
Слайд 11астрология (анализ расположения планет и созвездий);
биология (расшифровка кода ДНК);
военное дело (расположение
Слайд 12доставка почты (рассмотрение вариантов пересылки).
экономика (анализ вариантов купли-продажи акций);
криптография (разработка методов
Слайд 13Правило сложения:
Если некоторый объект А можно выбрать m способами, а другой
Пример:
На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?
Решение:
По условию задачи яблоко можно выбрать
пятью способами, апельсин – четырьмя.
Так как в задаче речь идет о выборе
«либо яблоко, либо апельсин», то его,
согласно правилу сложения, можно
осуществить 5+4=9 способами.
Ответ: 9 способов.
Слайд 14Задача:
Сколько двузначных чисел можно составить из цифр 1,4,7, используя в записи
1 способ: перебор вариантов.
Ответ: 6 чисел.
Решение:
Для того, чтобы не пропустить и не повторить ни одно из чисел, будем записывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4, и, наконец, с цифры 7:
14, 17, 41, 47, 71, 74.
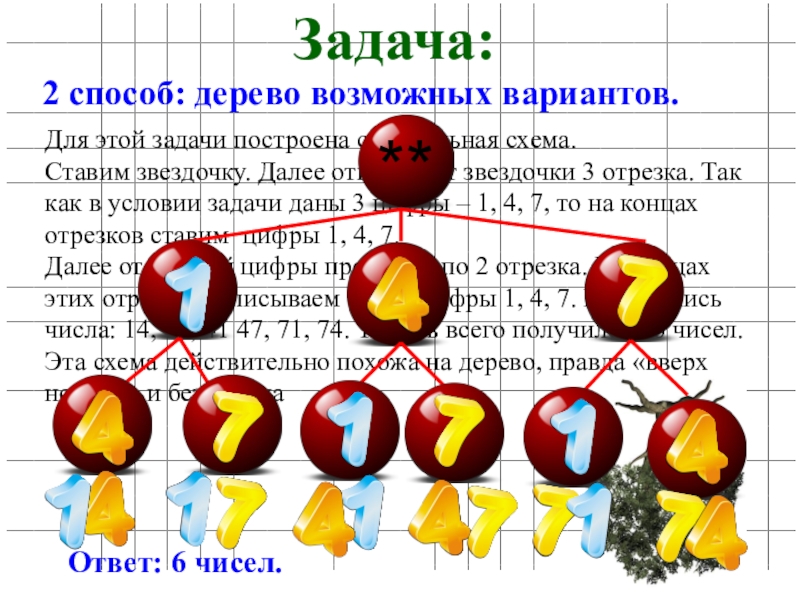
Слайд 15Задача:
2 способ: дерево возможных вариантов.
Для этой задачи построена специальная схема.
Ставим звездочку. Далее отводим от звездочки 3 отрезка. Так как в условии задачи даны 3 цифры – 1, 4, 7, то на концах отрезков ставим цифры 1, 4, 7.
Далее от каждой цифры проводим по 2 отрезка. На концах этих отрезков записываем также цифры 1, 4, 7. Получились числа: 14, 17, 41 47, 71, 74. То есть всего получилось 6 чисел. Эта схема действительно похожа на дерево, правда «вверх ногами» и без ствола
Ответ: 6 чисел.
Слайд 16Правило умножения:
Если объект А можно выбрать m способами и если после каждого такого
3 способ решения задачи:
Эту задачу можно решить по-другому и намного быстрее, не строя дерева возможных вариантов. Рассуждать будем так. Первую цифру двузначного числа можно выбрать тремя способами. Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать из оставшихся цифр уже двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 3∙2, т.е. 6.
Ответ: 6 чисел.
m-количество цифр стоящих на первом месте
n-количество цифр стоящих на втором месте
m∙n=3∙2=6
Слайд 17Задача 1
Сколько различных двузначных чисел можно записать с помощью
Решение:
m = 3, n = 4;
Ответ: 12
Задача 2
Сколько различных трехзначных чисел можно записать с помощью цифр 0, 1, 2, 3?
Решение:
m=3, n=4, k=4;
Ответ: 48
Задача 3
Сколько различных пятибуквенных слов можно записать с помощью букв «и» и «л»?
Решение:
a = 2, b = 2, c = 2, d = 2, f=2;
Ответ: 32
= 32
Л и л и и
2 • 2 • 2 • 2 • 2 =
abcdf =
m • n = 12
mnk=3 • 4 • 4
=48
Слайд 18Упражнения:
№ 1043
Сколько различных двузначных чисел с разными цифрами можно записать, используя
1вариант: 1) 1, 2 и 3; 3) 5, 6, 7 и 8; 5) 0, 2, 4 и 6;
2 вариант: 2) 4, 5, и 6; 4) 6, 7, 8 и 9; 6) 0, 3, 5 и 7?
Ответ: 1), 2) 6; 3), 4) 12; 5), 6) 9.
Сколько различных трехзначных чисел можно записать с помощью цифр:
1 вариант: 1) 2 и 3; 3) 0 и 2;
2 вариант: 2) 8 и 9; 4) 0 и 5?
Ответ: 1), 2) 8; 3),4) 4.
№ 1044
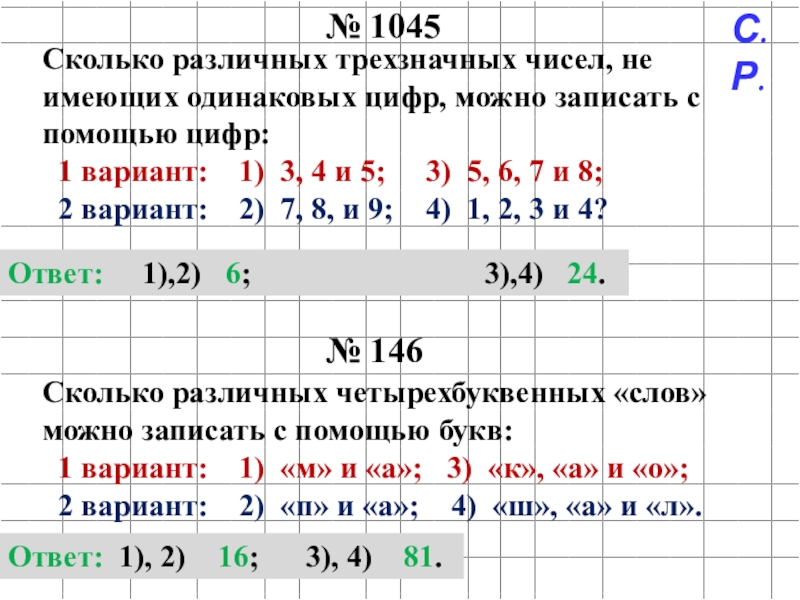
Слайд 19№ 1045
Сколько различных трехзначных чисел, не имеющих одинаковых цифр, можно записать
1 вариант: 1) 3, 4 и 5; 3) 5, 6, 7 и 8;
2 вариант: 2) 7, 8, и 9; 4) 1, 2, 3 и 4?
Ответ: 1),2) 6; 3),4) 24.
№ 146
Сколько различных четырехбуквенных «слов» можно записать с помощью букв:
1 вариант: 1) «м» и «а»; 3) «к», «а» и «о»;
2 вариант: 2) «п» и «а»; 4) «ш», «а» и «л».
Ответ: 1), 2) 16; 3), 4) 81.
С.Р.
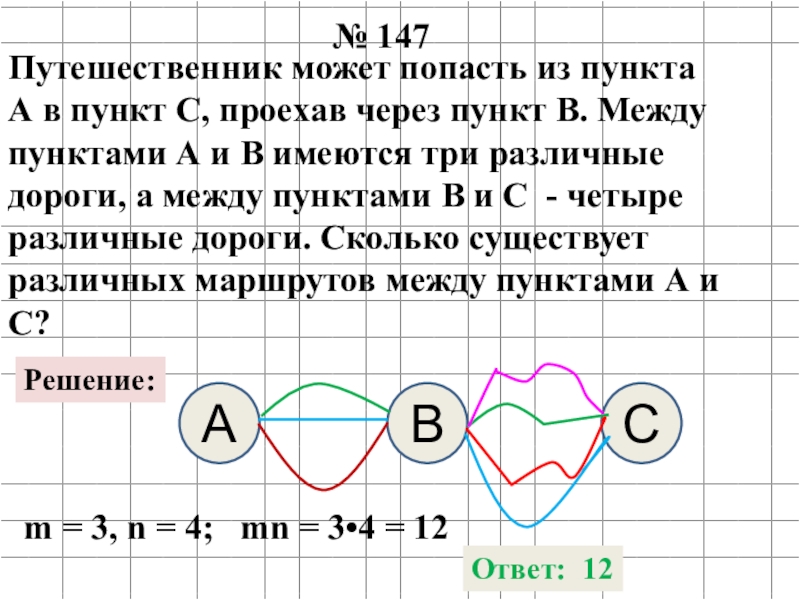
Слайд 20№ 147
Путешественник может попасть из пункта А в пункт С, проехав
Решение:
m = 3, n = 4; mn = 3•4 = 12
Ответ: 12
Слайд 21№ 1048
Чтобы попасть из города М в город К, нужно проехать
Ответ: 8
С.Р.
Дополнительно
Слайд 22№ 1049
№ 1050
№ 1052
1) 992 2) 240
120
1)
Сколькими способами могут распределиться золотая и серебряная медали на чемпионате по футболу, если в нем принимают участие:
1) 32 команды; 2) 16 команд?
Сколькими способами можно составить расписание 5 уроков на один день из 5 различных предметов?
Сколькими способами могут занять очередь в школьный буфет:
1) 6 учащихся; 2) 5 учащихся?
Дополнительно
Слайд 23№ 1053
№ 1054
№1055
В классе 18 учащихся. Из их числа нужно выбрать
В классе 20 учащихся. Необходимо назначить по одному дежурному в столовую, вестибюль и спортивный зал. Сколькими способами это можно сделать?
Сколько существует пятизначных чисел, в которых все цифры, стоящие на нечетных местах, различны?
4896
6840
64800
Слайд 24Факториал.
Таблица факториалов:
Определение. Факториалом натурального числа n называется произведение всех натуральных чисел
Слайд 27Упростить формулу записи выражений (полагая, что k-натуральное число, k>6)
Упражнения:
№ 1
№ 2
Ответ:
11!;
18!.
Ответ:
22!;
27!.
№ 3
Ответ:
(k+1)!;
k!.
Слайд 30Перестановками из n элементов называются соединения (комбинации), которые состоят из одних
Задача 1:
Сколькими способами можно поставить рядом на полке 4 различные книги?
Ответ:
24
Х
Х
Х
Определение.
Слайд 31Число перестановок:
(1)
Произведение первых n натуральных чисел обозначают
n! (читается «эн
n! = 123(n –2)(n–1)n
Pn = n(n –1)(n – 2)321
(2)
Pn = n!
(3)
Слайд 32 № 1059 Найти значение:
1) P5 =
№ 1060 Сколькими способами можно рассадить четверых детей на четырех стульях в столовой?
№ 1063 Сколько различных чисел, не содержащих одинаковых цифр, можно записать с помощью цифр 1,2,3,4,5 так, чтобы:
1) последней была цифра 3;
3) первой была цифра 5, а второй – цифра 1;
5) первыми были цифры 3 и 4, расположенные в любом порядке?
Упражнения:
№№ 1064 - 1071
Слайд 33Пример 1.
Сколькими способами могут быть расставлены восемь участниц финального забега
Решение: P8 = 8! = =40 320
Пример 2.
Сколько различных четырёхзначных чисел можно составить из цифр 0, 1, 2, 3, причём в каждом числе цифры должны быть разные?
Решение: P4 = 4! = =24,
Р4 – Р3 = 4! – 3! = 18
P3 = 3! = =6,
Слайд 34Пример 3.
Имеется 10 различных книг, среди которых есть трёхтомник одного
Решение:
Слайд 35Перестановки с повторениями.
Определение .
Число перестановок n – элементов, в котором
Задача: Сколько слов можно составить, переставив буквы в слове «экзамен», а в слове «математика»?
Решение: экзамен – 7 букв ( без повт.) ,
Математика - 10 букв ( с повт. м=2,а=3,т=2,е=и=к=1) ,
Слайд 37Задача 1.
Сколько различных двузначных чисел можно записать с помощью цифр 1,
Решение:
1 способ – решение перебором:
12, 13, 14,
21, 23, 24,
31, 32, 34,
41, 42, 43.
2 способ – по правилу произведения: m = 4, n = 3; mn = 12
Ответ: 12
Из задачи видно, что любые два соединения отличаются либо составом элементов (12 и 24), либо порядком их расположения (12 и 21). Такие соединения называют размещениями.
Слайд 38Размещениями из m элементов по n элементов (n ≤ m) называются
Обозначение:
читают «А из эм по эн»:
= 12.
Слайд 39= m(m – 1)(m – 2) • … • (m –
Примеры:
= 4 • 3 = 12;
= 4 • 3 • 2 = 24;
= 5 • 4 • 3 = 60
=
Задача 2.
Сколькими способами можно обозначить данный вектор, используя буквы A, B, C, D, E, F?
Решение:
(1)
(2)
или
Слайд 41Задача 5.
Из 12 учащихся нужно отобрать по одному человеку для
Решение:
Слайд 42Задача 6.
Сколько существует семизначных телефонных номеров, в которых все цифры
Решение:
Задача 7.
Сколько существует трёхзначных чисел, составленных из цифр 1, 2, 3, 4, 5, 6 (без повторений), которые НЕ кратны 3?
Решение:
Слайд 43Размещения с повторениями.
Определение.
k – размещением с повторениями n–элементного множества называется упорядоченный
Пример.
2- размещения с повторениями:
Число k – размещений с повторениями вычисляется по формуле:
Задача: Сколько существует номеров машин?
Слайд 45Определение. Подмножества, составленные из n элементов данного множества и содержащие k
Слайд 49Пример 1.
Сколькими способами можно выбрать трёх дежурных из класса, в
Решение:
Слайд 50Пример 2.
Из вазы с цветами, в которой стоят 10 красных
Решение:
Слайд 51 Пример 3.
Семь огурцов и три помидора надо положить в два
Решение:
Слайд 52«Би»-удвоение, раздвоение …
«Ном»(фран. nombre) –номер, нумерация.
«Бином» -»два числа»
Бином Ньютона – это
Треугольником Паскаля пользуются при возведении бинома в натуральные степени.
Бином Ньютона.
Слайд 532) Число всех членов разложения на единицу больше показателя степени бинома,
3) Сумма показателей степеней a и b каждого члена разложения равна показателю степени бинома,
то есть n.
4) Биномиальные коэффициенты членов разложения, равноотстоящих от концов разложения, равны между собой:
(правило симметрии).
Свойства бинома и биномиальных коэффициентов.
Слайд 545) Сумма биномиальных коэффициентов всех членов разложения равна
6) Сумма биномиальных коэффициентов, стоящих на нечетных местах, равна сумме биномиальных коэффициентов, стоящих на четных местах и равна
7) Правило Паскаля: .
Свойства бинома и биномиальных коэффициентов.
Слайд 558)Любой биномиальный коэффициент, начиная со второго, равен произведению предшествующего биномиального коэффициента
Свойства бинома и биномиальных коэффициентов.
Слайд 56Пример .
Доказать, что при любом натуральном n число
Доказательство:
Начнем рассматривать бином в общем виде:
Тогда
Слайд 60Различие между перестановками, размещениями, сочетаниями
В случае перестановок берутся все элементы и
В случае размещений берётся только часть элементов и важно расположение элементов друг относительно друга.
В случае сочетаний берётся только часть элементов и не имеет значения расположение элементов друг относительно друга.
Слайд 61Проверь себя
Что такое комбинаторика?
В чём состоит правило суммы?
В чём состоит
Что такое размещения?
Запишите формулу для нахождения числа размещений.
Что такое перестановки?
Запишите формулу для нахождения числа перестановок.
Что такое факториал?
Что такое сочетания?
Запишите формулу для нахождения числа сочетаний.
В чём различие между перестановками, размещениями, сочетаниями?
Слайд 68Электронные ресурсы:
кубики: http://free-math.ru/load/prezentacii_egeh_po_matematike/verojatnost_i_kombinatornoe/38-1-0-173
http://ru.gde-fon.com/cvety?offset[0]=648
http://ru.gde-fon.com/cvety?offset[0]=666
http://ru.gde-fon.com/cvety?offset[0]=4590
шаблон:
http://www.myshared.ru/slide/56405/
Санкт-Петербург, 2014



























































![Презентация по математике на тему Элементы комбинаторики Электронные ресурсы: кубики: http://free-math.ru/load/prezentacii_egeh_po_matematike/verojatnost_i_kombinatornoe/38-1-0-173 лилии:http://ru.gde-fon.com/cvety?offset[0]=648http://ru.gde-fon.com/cvety?offset[0]=666http://ru.gde-fon.com/cvety?offset[0]=4590шаблон:http://www.myshared.ru/slide/56405/Санкт-Петербург, 2014 Электронные ресурсы: кубики: http://free-math.ru/load/prezentacii_egeh_po_matematike/verojatnost_i_kombinatornoe/38-1-0-173 лилии:http://ru.gde-fon.com/cvety?offset[0]=648http://ru.gde-fon.com/cvety?offset[0]=666http://ru.gde-fon.com/cvety?offset[0]=4590шаблон:http://www.myshared.ru/slide/56405/Санкт-Петербург, 2014](/img/thumbs/757fd49c84ce48364d411828e9eeab79-800x.jpg)





