- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему ЕГЭ Задача № 19-теория чисел часть 2 (11 класс)
Содержание
- 1. Презентация по математике на тему ЕГЭ Задача № 19-теория чисел часть 2 (11 класс)
- 2. Почему же задача №19 считается (и, в
- 3. Числовые множестваРациональные числа2Иррациональные числа3Действительные числа4
- 4. Натуральные и целые числа1, 2, 3, 4,
- 5. Обозначения Факториал: n! = 1 ∙ 2
- 6. Простейшие примеры
- 7. Задумано несколько целых чисел. Набор этих чисел
- 8. Решение: а) Дополнительная информация: Если задумано n
- 9. Каждое из чисел 1, -2, -3, 4,
- 10. Решение: а) это невозможно, так как в
- 11. Рациональные числаЛюбое рациональное число можно записать в
- 12. Рациональные числаВерно и обратное утверждение:Любую бесконечную десятичную периодическую дробь можно представить в виде обыкновенной дроби.
- 13. Записать в виде обыкновенной дроби бесконечную десятичную
- 14. Записать в виде обыкновенной дроби бесконечную десятичную
- 15. Простейшие примеры
- 16. Задача №19 ЕГЭ-2018
- 17. Задача №19 ЕГЭ-2018
- 18. Задача №19 ЕГЭ-2018
- 19. Задача №19 ЕГЭ-2018
- 20. Задача №19 ЕГЭ-2018
- 21. Задача №19 ЕГЭ-2018
- 22. Задача №19 ЕГЭ-2018
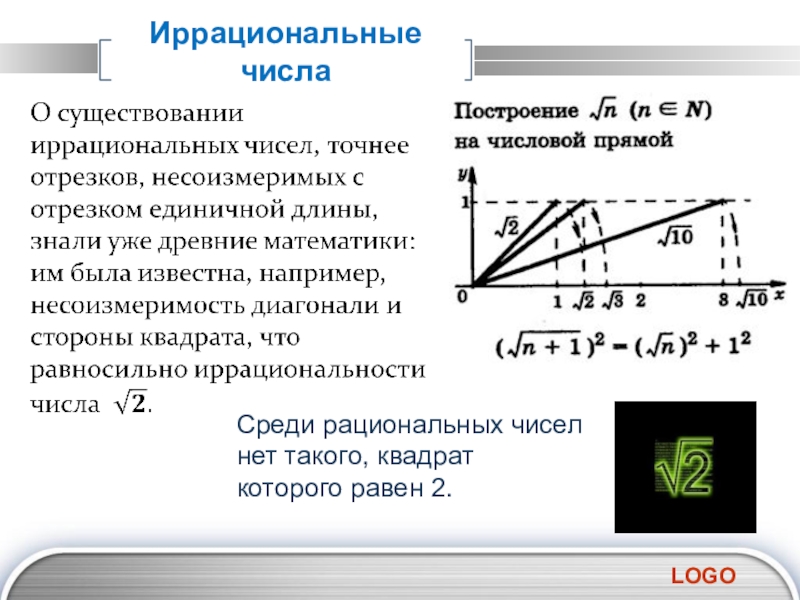
- 23. Иррациональные числа
- 24. Иррациональные числа
- 25. Среди рациональных чисел нет такого, квадрат которого равен 2.Иррациональные числа
- 26. Иррациональные числа
- 27. Все рациональные и иррациональные числа образуют множество
- 28. Если к положительным бесконечным десятичным дробям (периодическим
- 29. Слайд 29
Слайд 2Почему же задача №19 считается
(и, в общем-то, является) самой сложной
Она нестандартна.
Она требует математической культуры — умения грамотно строить рассуждения.
Учиться культурно рассуждать можно и обязательно нужно.
Задача №19 предоставляет для этого отличную возможность.
Надо мыслить
нестандартно
Слайд 4Натуральные и целые числа
1, 2, 3, 4, 5, 6, 7, 8,
ряд натуральных чисел N или (Z+)
-1, -2, -3, -4, -5, -6, -7, -8, -9, -10, -11, … –
ряд противоположных натуральным чисел Z–
…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, … –
ряд целых чисел Z (Z+ и Z– и 0)
Слайд 5Обозначения
Факториал: n! = 1 ∙ 2 ∙ 3 ∙ 4
Примеры: 6! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 = 720
2! = 1 ∙ 2 = 2
1! = 1
0! = 1
Слайд 7Задумано несколько целых чисел. Набор этих чисел и их все возможные
а) На доске выписан набор : -11; -7; -5; -4; -1; 2; 6. Какие числа были задуманы?
б) Для некоторых задуманных различных чисел в наборе, выписанном на доске, число 0 встречается ровно 4 раза. Какое наименьшее количество чисел было задумано?
в) Для некоторых задуманных чисел на доске выписан набор. Всегда ли можно по этому набору однозначно определить задуманные числа?
Ответ: а) -7, - 4, 6; б) 5; в) нет (см. решение далее)
А теперь задачи уровня ЕГЭ…
Слайд 8Решение: а) Дополнительная информация:
Если задумано n чисел, то объём набора
Ведь, по сути, мы рассматриваем всевозможные подмножества n-элементного множества (а их всего 2n ), за исключением пустого множества. Если задумано три числа, то набор состоит из семи чисел; Допустим, что задуманы одно отрицательное число a и два положительных.
Пусть а = -11. Поскольку все остальные числа набора должны быть больше a. Но тогда задумано число 2 ( -11 + 2 = -9), а его нет в наборе, или задумано число 6 ( -11 + 6 = -5), это число есть в наборе, но другого положительного, большего 6 нет. Противоречие показывает, что задуманы два отрицательных числа и одно положительное.
Подходит -7, - 4, 6.
б) Пусть задуманы три числа. Четырех нулей среди них быть не может, поскольку среди задуманных чисел возможен набор из 0 и двух противоположных чисел, тогда появятся только три нуля. Пусть задуманы четыре числа. Опять могут появиться только три 0.
Две пары противоположных чисел могут дать нам три 0. Другие варианты – это такой же случай, как с тремя задуманными числами. Если задуманы пять чисел, то четыре 0 в полученном наборе возможен. Например, две пары противоположных чисел и 0.
в) задуманные числа не всегда можно однозначно восстановить по набору. Например, задумаем сначала числа -3, 1, 2, а потом числа 3, - 1, -2. В обоих случаях получим один и тот же набор -3, -2, -1, 0, 1, 2, 3. Взяли числа, дающие в сумме нуль, а потом поменяли у них знаки — набор не изменился.
А теперь задачи уровня ЕГЭ…
Слайд 9Каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9,
на 10 карточках. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 1, -2, -3, 4, -5, 7, -8, 9, 10, -11. После этого числа на каждой карточке складывают, а полученные 10 сумм перемножают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Какое наименьшее целое неотрицательное число может в результате получиться?
Ответ: а) нет; б) нет; в) 4 (см. решение далее)
А теперь задачи уровня ЕГЭ…
Слайд 10Решение: а) это невозможно, так как в данном наборе ни для
нет ему противоположного по знаку, нет ни одного множителя, равного 0. Значит, 0 в произведении получиться не может.
б) в произведении каждый множитель должен быть нечётным, чтобы в результате получилось нечетное число.
Следовательно, для каждого числа в паре должно быть одно число чётное, а другое нечётное. Однако из условия вытекает, что указанная последовательность содержит 4 чётных числа и 6 нечётных. Делаем вывод, что два множителя обязательно будут чётными, значит и произведение обязательно будет четным. В частности, 1 получиться не может.
в) а = (1 - 2)( -2 + 1)( -3 + 4)(4 - 3)( -5 + 7)(7 - 5)( -8 + 9)(9 - 8)(10 - 11)( -11 + 10) = 4:
Следовательно, наименьшее неотрицательное значение равно 4. (Логика возможного набора чисел на карточках понятна – суммы должны принимать наименьшие значения).
А теперь задачи уровня ЕГЭ…
Слайд 11Рациональные числа
Любое рациональное число можно записать в виде конечной десятичной дроби
Рациональные числа – это числа вида ,
где m – целое число, а n – натуральное.
Q - множество рациональных чисел.
Примеры:
6 = 6,000… = 6,(0); 7,432 = 7,432000… = 7,432(0).
= 0,17(857142); = 0,(285714);
Слайд 12Рациональные числа
Верно и обратное утверждение:
Любую бесконечную десятичную периодическую дробь можно представить
Слайд 13Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь :
Пусть х
Умножим х на 100, чтобы запятая переместилась вправо на один период:
100х = 123,232323…
х = 1,232323…
100х – х = 122,000000…
Т.е. 99х = 122, откуда х =
Пример (1 способ):
–
Простейшие примеры
Слайд 14Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь :
Пусть 1,(23)
Рассмотрим эту сумму 1 и суммы бесконечно убывающей геометрической прогрессии: S = 1 + S1, где S1 = b1 / (1 – q) – формула суммы бесконечно убывающей прогрессии со знаменателем q = 0,01, и первым членом b1 = 0,23:
S1 = =
S = 1 + =
Пример (2 способ):
Простейшие примеры
Слайд 27Все рациональные и иррациональные числа образуют множество действительных чисел, которое обозначают
Иррациональные и действительные числа
Термины «рациональное число», «иррациональное число» происходят от латинского слова ratio – разум (буквальный перевод: «рациональное число – разумное число», «иррациональное число – неразумное число»).
Примеры:
Слайд 28Если к положительным бесконечным десятичным дробям (периодическим и непериодическим) присоединить противоположные
Множество действительных чисел состоит из рациональных и иррациональных чисел.
Все рациональные и иррациональные числа образуют множество действительных чисел, которое обозначают R.
Действительные числа