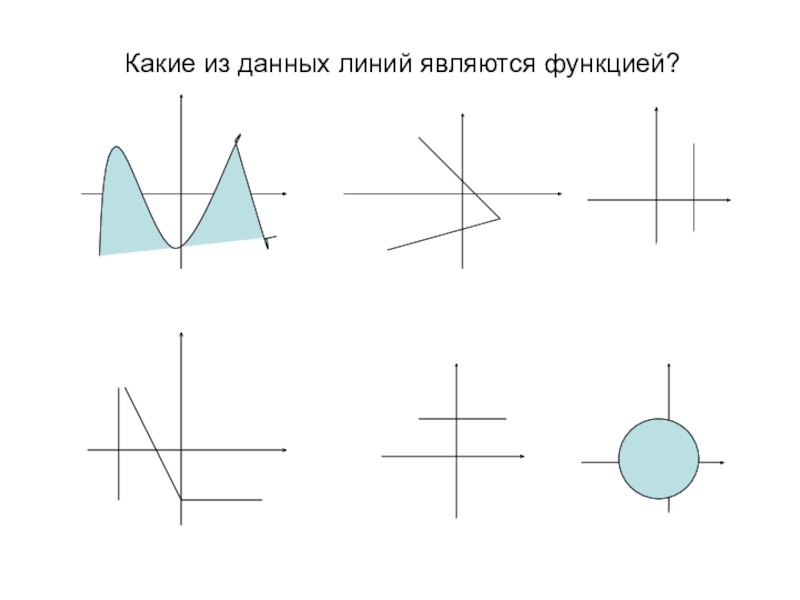
Пишут: у = f(x), x Є X.
Переменную х называют независимой переменной или аргументом.
Множество всех допустимых значений независимой переменной является областью определения функции и обозначается D(y).
Переменную у – зависимой переменной.
Множество всех значений зависимой переменной является областью значений функции и обозначается Е(у).

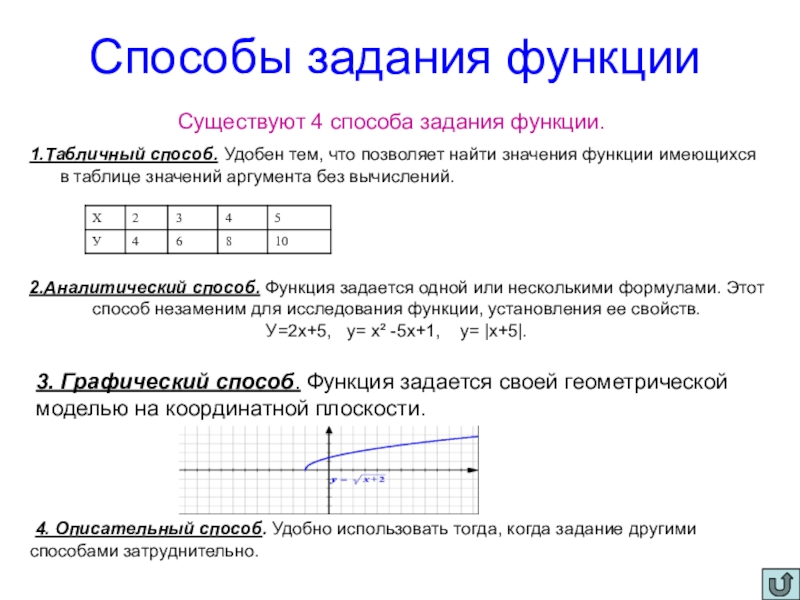

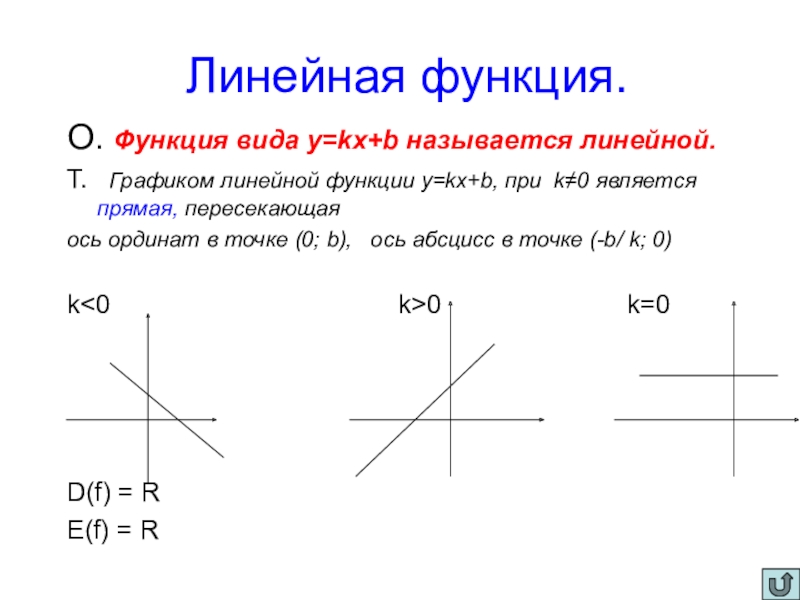
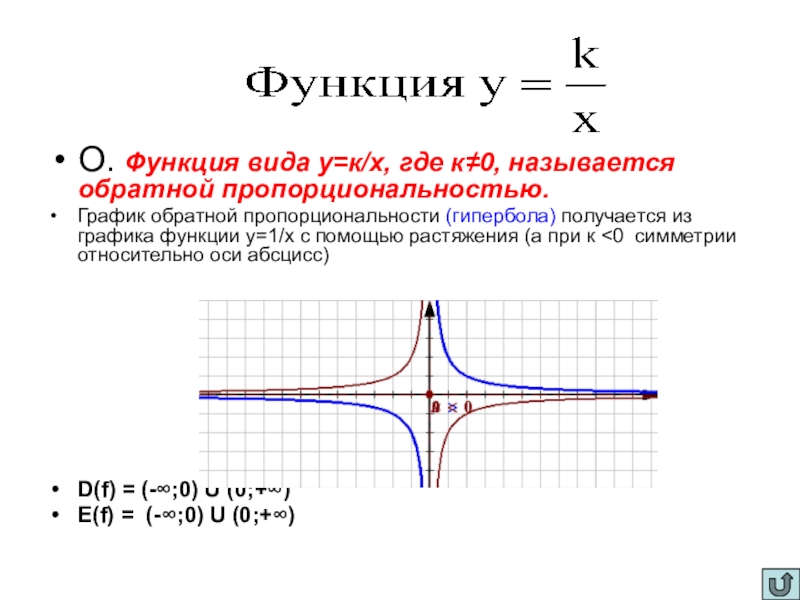


![Презентация по математике на тему Числовые функции (10 класс) Функция задана графиком. Укажите область определения. Ответ:X Є [1;5]Ответ:X Є [-1;8] Функция задана графиком. Укажите область определения. Ответ:X Є [1;5]Ответ:X Є [-1;8]](/img/thumbs/856ad4ed83e3344dae213720d23b04d8-800x.jpg)

![Презентация по математике на тему Числовые функции (10 класс) На рисунке изображен график функции у =f(x), заданной на отрезке [-4;7]. На рисунке изображен график функции у =f(x), заданной на отрезке [-4;7]. Укажите те значения х, для которых](/img/thumbs/aedd79961fb4cf1b4f547b6c0b21430c-800x.jpg)