- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Числовая последовательность
Содержание
- 1. Презентация по математике на тему Числовая последовательность
- 2. Раздел математики
- 3. 1. Числовая последовательностьОпределение:
- 4. Пример: у = 5, где
- 5. Способы задания: 1) словесный;
- 6. Рекуррентный –формула n – го члена
- 7. А.С.Пушкин
- 8. Свойства последовательностейОграничена сверху, если все её члены
- 9. Свойства последовательностейВозрастающая – каждый член последовательности
- 10. 2. Предел числовой последовательностиОпределение :
- 11. Пример: yn = , где
- 12. Пример: yn = ( )n
- 13. Свойство предела последовательности
- 14. Пример: f(x)= , где
- 15. 3. Вычисление пределов последовательности Формулы :
Слайд 2Раздел математики
Цель : изучение поведения функции в конкретной точке
Новые понятия : предел, производная
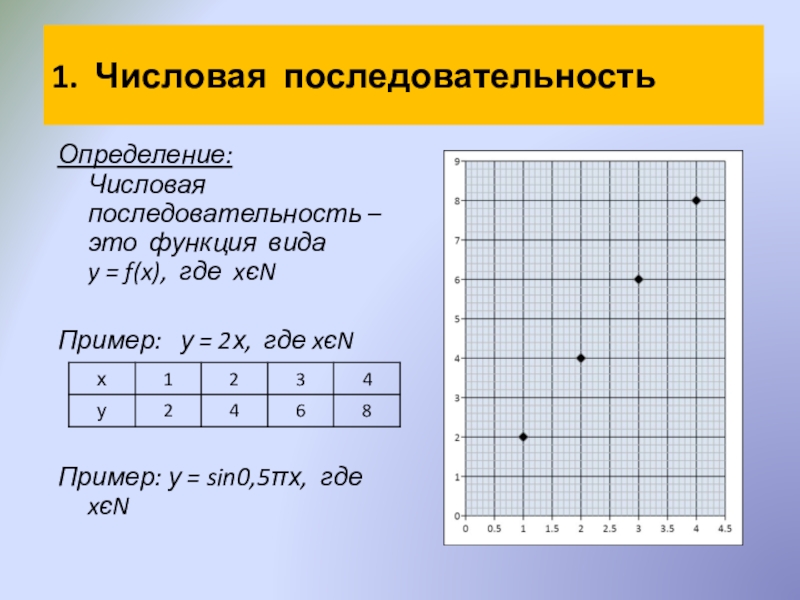
Слайд 31. Числовая последовательность
Определение: Числовая
Пример: у = 2х, где xєN
Пример: у = sin0,5х, где xєN
Слайд 4
Пример: у = 5, где xєN
у = С,
такая последовательность называется постоянной или стационарной
Слайд 5Способы задания: 1) словесный;
Аналитический – задана формула n – го члена прогрессии
Пример: y = 2n²
y₁ = 2·1² = 2, y₃ = 2·3² = 18 ,
y = 450, то n = ?
n = 15
Пример: y = 3,7n – 1,5
y₁ = 3,7·1 – 1,5 = 2,2
y10 = 3,7·10 – 1,5 = 35,5
Пример: по учебнику 24.1-2-3(а,б)
Слайд 6Рекуррентный –формула n – го члена связана с предыдущими членами
Пример:
Арифметическая прогрессия yn = yn-1 + d , d – некоторое число ( разность)
yn = y1 + d· ( n – 1)
2) Геометрическая прогрессия
yn = yn-1 · q , q – некоторое число (знаменатель)
yn = 0, q = 0
Слайд 8Свойства последовательностей
Ограничена сверху, если все её члены не больше некоторого числа.
пример: -5; -10; -15; -20; -25 …
М = -5, то yn ≤ -5
2) Ограничена снизу, если все её члены не меньше некоторого числа.
yn ≥ т, т – нижняя граница
пример: 5; 10; 15; 20; 25 …
т = 5, то yn ≥ 5
3) Ограничена, если ограничена и сверху и снизу
т ≤ yn ≤ М,
т – нижняя граница, М – верхняя граница
Слайд 9Свойства последовательностей
Возрастающая – каждый член последовательности больше предыдущего
y1>y2>y3> … >yn>yn+1>…
6) Монотонная – возрастающая или убывающая
Слайд 102. Предел числовой последовательности
Определение :
число b называется
Обозначение : yn b при n ∞
Lim yn = b
n ∞
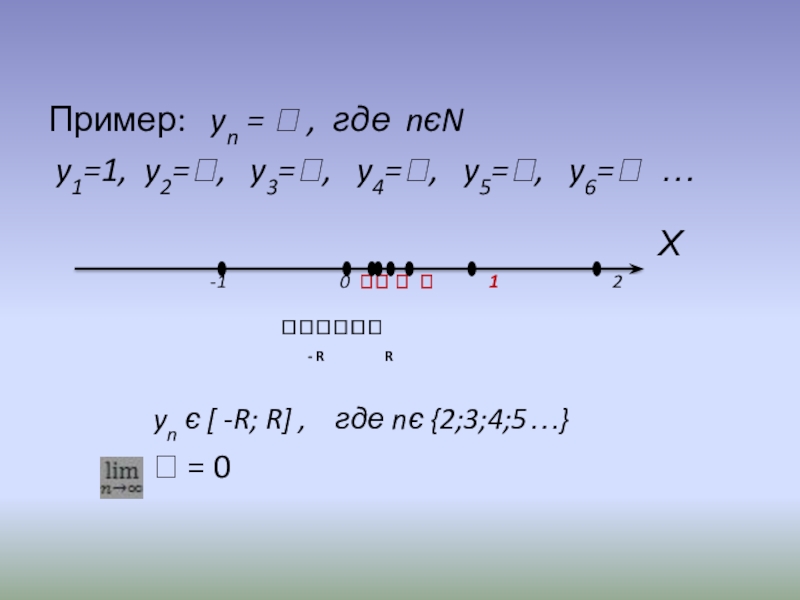
Слайд 11Пример: yn = , где nєN
y1=1, y2=,
Х
-1 0 1 2
- R R
yn є -R; R , где nє 2;3;4;5…
= 0
Слайд 12
Пример: yn = ( )n , где xєN
( )n = 0
Пример: yn = , где xєN
(yn ): 1; 1 ;1 ; 1 ; 1;…
-1 0 1 2 3 X
1 1 1 1
= 2
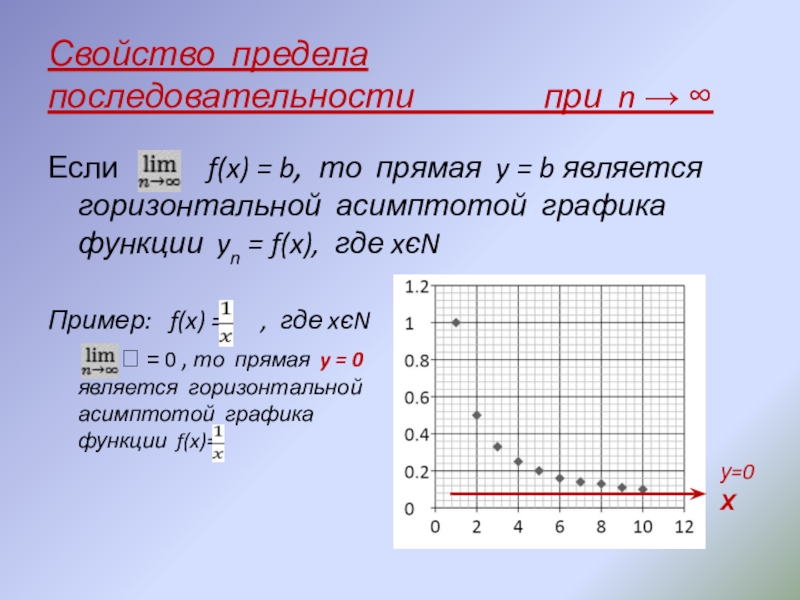
Слайд 13Свойство предела последовательности при
Если f(x) = b, то прямая y = b является горизонтальной асимптотой графика функции yn = f(x), где xєN
Пример: f(x) = , где xєN
= 0 , то прямая y = 0 является горизонтальной асимптотой графика функции f(x)=
у=0
Х
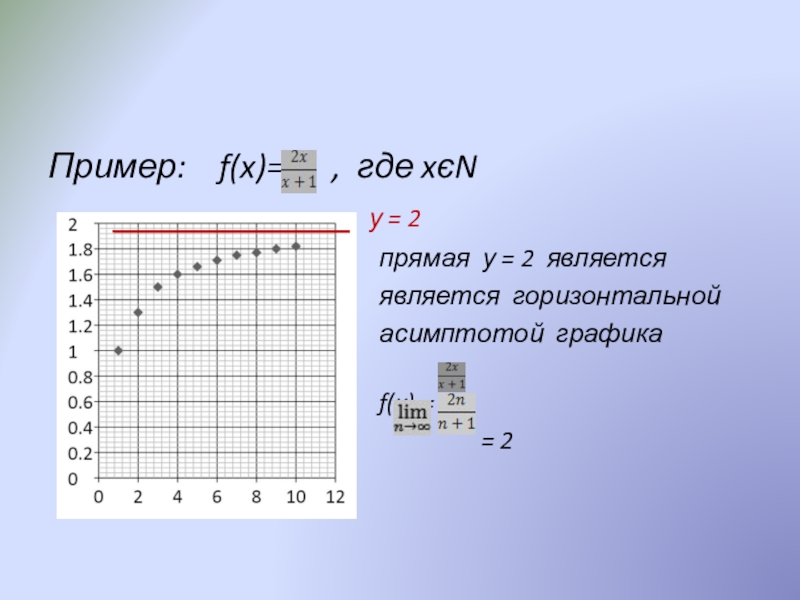
Слайд 14Пример: f(x)= , где xєN
прямая у = 2 является
является горизонтальной
асимптотой графика функции
f(x) =
= 2 функции f(x)=
Слайд 153. Вычисление пределов последовательности
Формулы : 1)
2) ()n = 0 ;
3) (q)n = 0, если |q|< 1
если |q|>1, то предел не существует
( последовательность расходится)
4) С = С