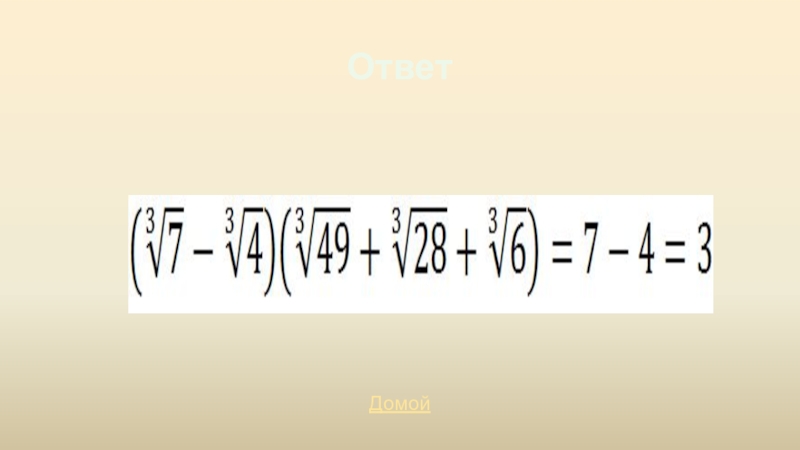- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Арифметический корень n-ой степени и его приложение.
Содержание
- 1. Презентация по математике на тему: Арифметический корень n-ой степени и его приложение.
- 2. Играть
- 3. 2030405020304050203040502030405020304050
- 4. Узнать ответВопросКто открыл квадратные корни?
- 5. ОтветНеобходимость математических вычислений при строительстве любых больших
- 6. Вопрос«Арифметика» Диофанта Узнать ответ
- 7. Ответ«Арифметика» Диофанта Спустя 600 лет в той
- 8. ВопросКвадратный корень из пирамиды ХеопсаУзнать ответ
- 9. ОтветКвадратный корень из пирамиды ХеопсаКак любое великое
- 10. ВопросМатематика на глиняных табличках Узнать ответ
- 11. ОтветМатематика на глиняных табличкахГород Вавилон (Врата Бога)
- 12. ВопросГде вы применяете понятие «КОРЕНЬ»?Фразеологизмы и устойчивые
- 13. ОтветСкрытая, заглублённая часть основания чего-либо, например органа живого
- 14. ВопросПонятие корня n-ой степени?Узнать ответ
- 15. ОтветКорнем n-ой степени из некоторого выражения называется
- 16. ВопросПравила вычисления корней четной и нечетной степеней.Узнать ответ
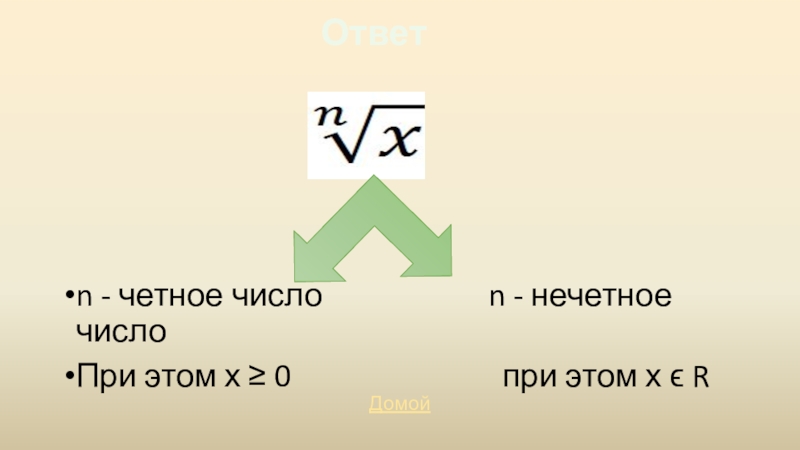
- 17. Ответn - четное число
- 18. ВопросПри каком условии выполняется равенство?Приведите пример.Узнать ответ
- 19. Ответ1. Когда n=m и x=yПример:2. Когда n - четное, а m - нечетное и выполняется условие:Домой
- 20. ВопросВычислить значение: Узнать ответ
- 21. ОтветДомой
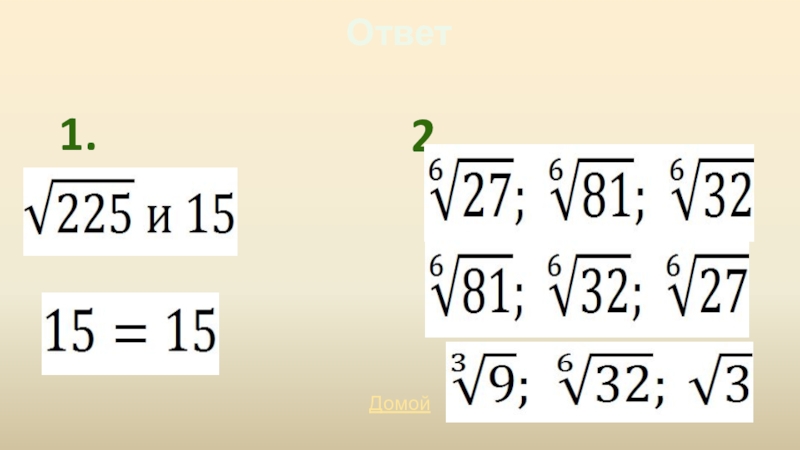
- 22. Вопрос1. Сравнить корни2. Поставить в порядке убывания1.2.Узнать ответ
- 23. Ответ1.2.Домой
- 24. ВопросИзбавиться от иррациональности в знаменателе.Узнать ответ
- 25. ОтветДомой
- 26. ВопросВычислитьУзнать ответ
- 27. ОтветДомой
- 28. ВопросОпределение иррационального уравнения.Приведите примеры.Правила, позволяющее решать иррациональные уравнения.Узнать ответ
- 29. ОтветУравнение, содержащее неизвестную переменную под знаком корня,
- 30. ВопросРешить уравнение:Узнать ответ
- 31. ОтветПроверка показала, что Домой
- 32. ВопросРешить уравнениеУзнать ответ
- 33. ОтветРешения нет, т.к. корень четной степени не может быть отрицательным числом. Домой
- 34. ВопросРешить уравнениеУзнать ответ
- 35. ОтветРешение.Введем замену: Тогда
- 36. ВопросРассмотрите первые шесть стандартных схем решения неравенств.Узнать ответ
- 37. ОтветДомой
- 38. ВопросРешите неравенствоУзнать ответ
- 39. Ответ: (-∞;-1) U [2;∞)Решение.Воспользуемся для решения схемой
- 40. ВопросРешите неравенство:Узнать ответ
- 41. Слайд 41
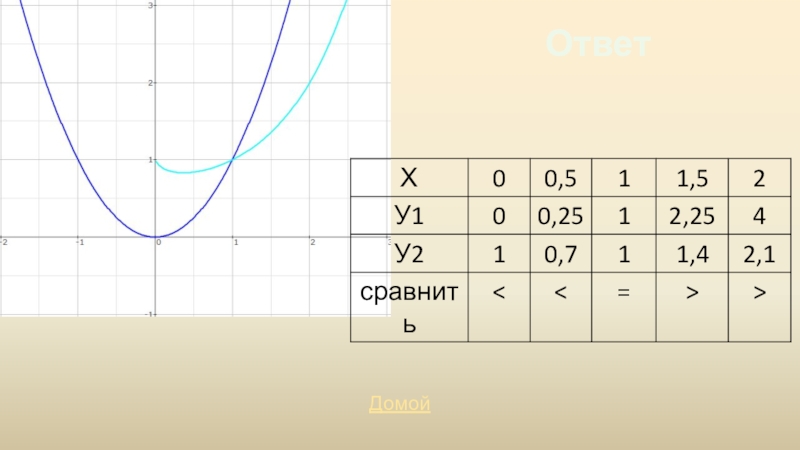
- 42. ВопросПостроить графики функций:Сравнить значения этих функций при следующем х:Узнать ответ
- 43. ОтветДомой
- 44. РЕФЛЕКСИЯ.1. Проследите в ответах историю развития корня.2.
- 45. СПАСИБО ЗА УРОК !
Играть
Слайд 5Ответ
Необходимость математических вычислений при строительстве любых больших сооружений определило появление квадратного
корня. Например, узнать длину диагонали любого прямоугольника возможно только, извлекая квадратный корень из суммы квадратов длин двух сторон.
Из всей истории появления в математике квадратного корня получается, что патент на изобретение квадратичных исчислений, так же, как и на изобретение колеса, выдавать некому.
Из всей истории появления в математике квадратного корня получается, что патент на изобретение квадратичных исчислений, так же, как и на изобретение колеса, выдавать некому.
Домой
Слайд 7Ответ
«Арифметика» Диофанта
Спустя 600 лет в той же Греции Диофант Александрийский, основываясь
на работах своих предшественников, ввел математические обозначения, которые человечество использует и сегодня, описал решения неопределенных уравнений, ввел понятия рациональных и иррациональных чисел. Им было написано 13 трактатов «Арифметика», только 6 из которых сохранились. В этих трудах великий грек объясняет решения уравнений с двумя неизвестными второго порядка, используя для их решений извлечение квадратного корня из числа, как давно известное математическое действии.
Домой
Слайд 9Ответ
Квадратный корень из пирамиды Хеопса
Как любое великое открытие, оно возникло одновременно
в нескольких местах в головах разных гениальных людей. Например, в 2500 гг. до н.э. в Древнем Египте возводились пирамиды – усыпальницы фараонов. Археологи просчитали, что без знания числа π и квадратного корня построить такие сооружения с четко выстроенными коридорами и строгой ориентацией помещений по сторонам света было просто невозможно. И снова даже граффити на стенах каменных блоков не донесли до современности имен гениальных математиков.
Домой
Слайд 11Ответ
Математика на глиняных табличках
Город Вавилон (Врата Бога) с населением полтора тысяч
человек был основан в Междуречье более 3000 лет до н.э. На раскопках этого древнего поселения были найдены глиняные таблички с нанесенными на них знаками. Их возраст превышает 5000 лет. Когда были расшифрованы символы клинописи, археологи с изумлением прочитали уравнения вычисления различных площадей с помощью квадратных корней. Не известие об открытии, а уже его использование. Имя великого математика, первым догадавшегося извлечь квадратный корень, утеряно в анналах истории.
Домой
Слайд 12Вопрос
Где вы применяете понятие
«КОРЕНЬ»?
Фразеологизмы и устойчивые сочетания:
в корень
вырывать с корнем
извлекать
корень
квадратный корень
корень зла
кубический корень
на корню
под корень
пустить корни
сладкий корень
квадратный корень
корень зла
кубический корень
на корню
под корень
пустить корни
сладкий корень
Узнать ответ
Слайд 13Ответ
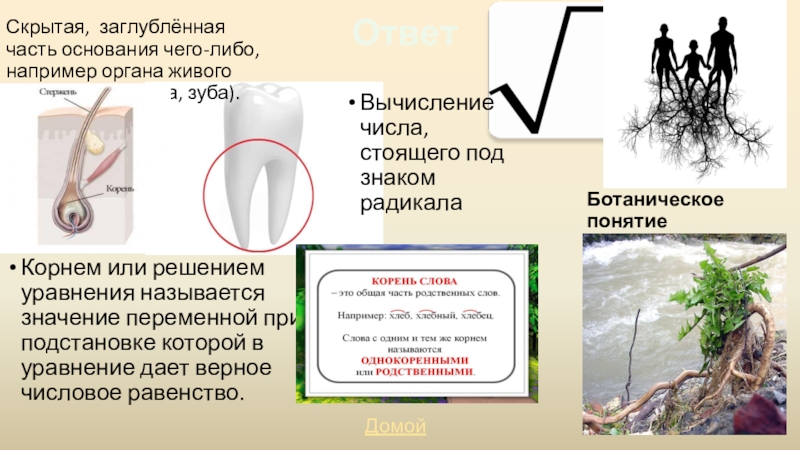
Скрытая, заглублённая часть основания чего-либо, например органа живого организма (волоса, зуба).
Корнем или
решением уравнения называется значение переменной при подстановке которой в уравнение дает верное числовое равенство.
Ботаническое понятие
Вычисление числа, стоящего под знаком радикала
Домой
Слайд 15Ответ
Корнем n-ой степени из некоторого выражения называется такое число, которое в
степени корня дает подкоренное выражение. При этом степень корня число натуральное, большее единицы.
Домой
Слайд 19Ответ
1. Когда n=m и x=y
Пример:
2. Когда n - четное, а m
- нечетное и выполняется условие:
Домой
Слайд 28Вопрос
Определение иррационального уравнения.
Приведите примеры.
Правила, позволяющее решать иррациональные уравнения.
Узнать ответ
Слайд 29Ответ
Уравнение, содержащее неизвестную переменную под знаком корня, называется иррациональным.
Правило 1:
Чтоб избавиться
от корня n-ой
степени в уравнении, необходимо
возвести обе части в степень корня.
Правило 2:
Корень четной степени – число
неотрицательное(положительное или
ноль).
Правило 3:
Сделай проверку!
степени в уравнении, необходимо
возвести обе части в степень корня.
Правило 2:
Корень четной степени – число
неотрицательное(положительное или
ноль).
Правило 3:
Сделай проверку!
Домой
Слайд 35Ответ
Решение.
Введем замену:
Тогда
и
Получим:
Получим:
Проверка показывает, что х=3 – корень уравнения.
Домой
Слайд 39Ответ: (-∞;-1) U [2;∞)
Решение.
Воспользуемся для решения схемой №3:
Корни первого неравенства:
Корни
второго неравенства:
(по теореме Виета)
(по теореме Виета)
Покажем решение обоих неравенств на чертеже.
Это параболы, ветви которых направлены вверх:
«+» -1 «+» 1 «+» 2 «+»
«-» «-» х
Домой
Слайд 41
Ответ :
Решение.
Воспользуемся для решения схемой №5
Хϵ(4;∞)
Первые два неравенства дают решение х ≥ 0
По теореме Виета находим корни третьего неравенства, и учитывая, что
это парабола, ветви которой
направлены вверх, получим
следующее изображение:
+ -3 0 4 + х
__
Домой
Слайд 44РЕФЛЕКСИЯ.
1. Проследите в ответах историю развития корня.
2. Приведите пример задач, где
используется корень.
3. Основные моменты при решении иррациональных уравнений.
4. Что труднее дается: «Решение уравнений или неравенств?»
5. Будем еще проводить такие уроки?
6. Оценим себя по количеству набранных баллов:
100-200 баллов – «3»
200-300 баллов – «4»
300- баллов – «5»
3. Основные моменты при решении иррациональных уравнений.
4. Что труднее дается: «Решение уравнений или неравенств?»
5. Будем еще проводить такие уроки?
6. Оценим себя по количеству набранных баллов:
100-200 баллов – «3»
200-300 баллов – «4»
300- баллов – «5»
