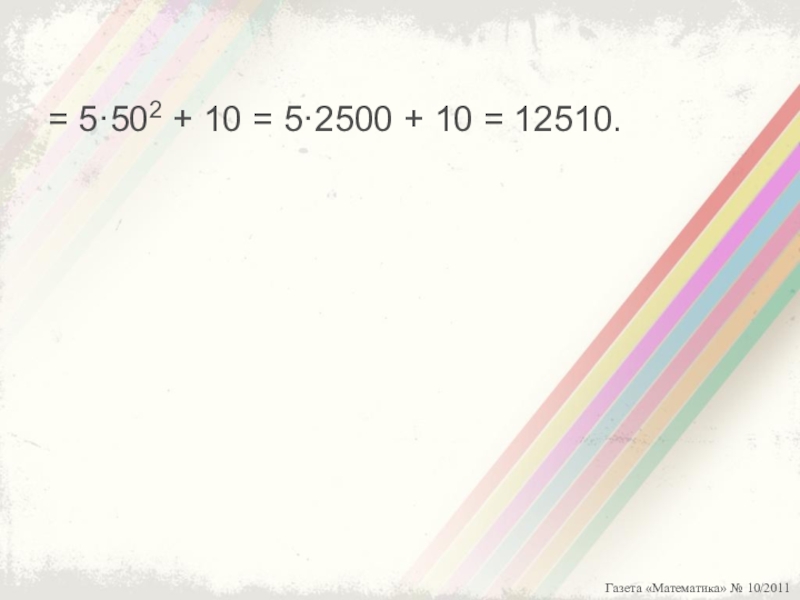- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Магия математики. Трудная задача
Содержание
- 1. Презентация по математике Магия математики. Трудная задача
- 2. Слайд 2
- 3. Слайд 3
- 4. Н. П. Богданов-БельскийУстный счёт. В народной школе С. А. Рачинского. 1895Холст, масло. 107,4 × 79 смГосударственная Третьяковская галереяГосударственная Третьяковская галерея, Москва
- 5. Сергей Александрович РачинскийДата рождения: 20 апреля (2
- 6. 102 + 112 + 122 + 132 + 142
- 7. Воспользуйтесь этим приемом и
- 8. = 5·502 + 10 = 5·2500 + 10 = 12510.
- 9. Усложним: 842 + 872 + 902 + 932 + 962 =
- 10. = 5·8100 + 2·9 + 2·36
- 11. Единственный ли это ряд из пяти последовательных
- 12. Удобнее обозначить через х не первое, а
- 13. Раскрыв скобки и сделав упрощения, получаем:
- 14. Существуют, следовательно, два ряда чисел, обладающих требуемым
Автопортрет, 1915Имя при рождении: Николай Петрович БогдановДата рождения: 8 декабря 8 декабря 1868Место рождения: д. Шитики, Бельский уезд, Смоленская губерния
Слайд 2
Автопортрет, 1915
Имя при рождении: Николай Петрович Богданов
Дата рождения: 8 декабря 8 декабря 1868
Место рождения: д. Шитики, Бельский уезд, Смоленская
губерния губерния, Россия
Дата смерти: 19 февраля 19 февраля 1945 (76 лет)
Место смерти: Берлин Берлин, Германия
Страна: Российская империя
Учёба: Императорская Академия художеств
Награды: Командор ордена Трех Звезд
Имя при рождении: Николай Петрович Богданов
Дата рождения: 8 декабря 8 декабря 1868
Место рождения: д. Шитики, Бельский уезд, Смоленская
губерния губерния, Россия
Дата смерти: 19 февраля 19 февраля 1945 (76 лет)
Место смерти: Берлин Берлин, Германия
Страна: Российская империя
Учёба: Императорская Академия художеств
Награды: Командор ордена Трех Звезд
Слайд 4
Н. П. Богданов-Бельский
Устный счёт. В народной школе С. А. Рачинского. 1895
Холст, масло. 107,4 × 79 см
Государственная Третьяковская
галереяГосударственная Третьяковская галерея, Москва
Слайд 5
Сергей Александрович Рачинский
Дата рождения: 20 апреля (2 мая 20 апреля (2
мая) 1833
Место рождения:с. Татево, Бельский уезд,Смоленская губернияс. Татево, Бельский уезд,Смоленская губерния,Российская империяс. Татево, Бельский уезд,Смоленская губерния,Российская империя, ныне Тверская область
Дата смерти:19 апреля (2 мая19 апреля (2 мая) 1902(69 лет)
Место смерти:с. Татево, Бельский уезд,Смоленская губернияс. Татево, Бельский уезд,Смоленская губерния,Российская империяс. Татево, Бельский уезд,Смоленская губерния,Российская империяныне Тверская область
Страна:Российская империя
Научная сфера: биология биология, математика биология, математика,педагогика
Место работы: Московский университет, Татевская сельская школа для крестьянских детей
Альма-матер: Московский университет
Известные ученики: Н. П. Богданов-Бельский
Известен как: педагог-энтузиаст, деятель в области народного образования, сторонник народной трезвости
Место рождения:с. Татево, Бельский уезд,Смоленская губернияс. Татево, Бельский уезд,Смоленская губерния,Российская империяс. Татево, Бельский уезд,Смоленская губерния,Российская империя, ныне Тверская область
Дата смерти:19 апреля (2 мая19 апреля (2 мая) 1902(69 лет)
Место смерти:с. Татево, Бельский уезд,Смоленская губернияс. Татево, Бельский уезд,Смоленская губерния,Российская империяс. Татево, Бельский уезд,Смоленская губерния,Российская империяныне Тверская область
Страна:Российская империя
Научная сфера: биология биология, математика биология, математика,педагогика
Место работы: Московский университет, Татевская сельская школа для крестьянских детей
Альма-матер: Московский университет
Известные ученики: Н. П. Богданов-Бельский
Известен как: педагог-энтузиаст, деятель в области народного образования, сторонник народной трезвости
Слайд 6
102 + 112 + 122 + 132 + 142
365
Числа 10, 11, 12, 13 и 14 обладают любопытной особенностью:
102 + 112 + 122 = 132 + 142.
Действительно, так как
100 + 121 + 144 = 169 + 196 = 365
Числа 10, 11, 12, 13 и 14 обладают любопытной особенностью:
102 + 112 + 122 = 132 + 142.
Действительно, так как
100 + 121 + 144 = 169 + 196 = 365
Слайд 11
Единственный ли это ряд из пяти последовательных чисел,
сумма квадратов первых
трех из которых
равна сумме квадратов двух последних?
Обозначив первое из искомых чисел через x, имеем уравнение
x2 + (х + 1)2 + (x + 2)2 = (x + 3)2 + (x + 4)2.
равна сумме квадратов двух последних?
Обозначив первое из искомых чисел через x, имеем уравнение
x2 + (х + 1)2 + (x + 2)2 = (x + 3)2 + (x + 4)2.
Слайд 12
Удобнее обозначить через х не первое, а второе из искомых чисел.
Тогда уравнение будет иметь более простой вид
(x – 1)2 + x2 + (x + 1)2 = (x + 2)2 + (x + 3)2.
(x – 1)2 + x2 + (x + 1)2 = (x + 2)2 + (x + 3)2.
Слайд 13
Раскрыв скобки и сделав упрощения, получаем:
x2 – 10x – 11 = 0,
X2 - 2х+5 + 25 – 25 – 11 = 0,
(X – 5)2 - 36 = 0,
(х-5-6)(х-5+6)=0,
(х – 11)(х – 1) = 0,
х1 = 11, x2 = –1
X2 - 2х+5 + 25 – 25 – 11 = 0,
(X – 5)2 - 36 = 0,
(х-5-6)(х-5+6)=0,
(х – 11)(х – 1) = 0,
х1 = 11, x2 = –1
Слайд 14
Существуют, следовательно, два ряда чисел, обладающих требуемым свойством: ряд Рачинского
10, 11, 12, 13, 14
и ряд
–2, –1, 0, 1, 2.
В самом деле,
(–2)2 +(–1)2 + 02 = 12 + 22.
Два!!!
и ряд
–2, –1, 0, 1, 2.
В самом деле,
(–2)2 +(–1)2 + 02 = 12 + 22.
Два!!!