- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Линейные и квадратичные неравенства, 10 класс
Содержание
- 1. Презентация по математике Линейные и квадратичные неравенства, 10 класс
- 2. Linear InequalitiesThese inequalities can be solved like
- 3. Linear InequalitiesThese inequalities can be solved like
- 4. Divide by −4:Solution:Divide by 3e.g.2 Find the
- 5. ExercisesFind the range of values of x
- 6. Quadratic InequalitiesSolution:Rearrange to get zero on one
- 7. Solution:There are 2 sets of values of xThese represent 2 separate intervals and CANNOT be combined
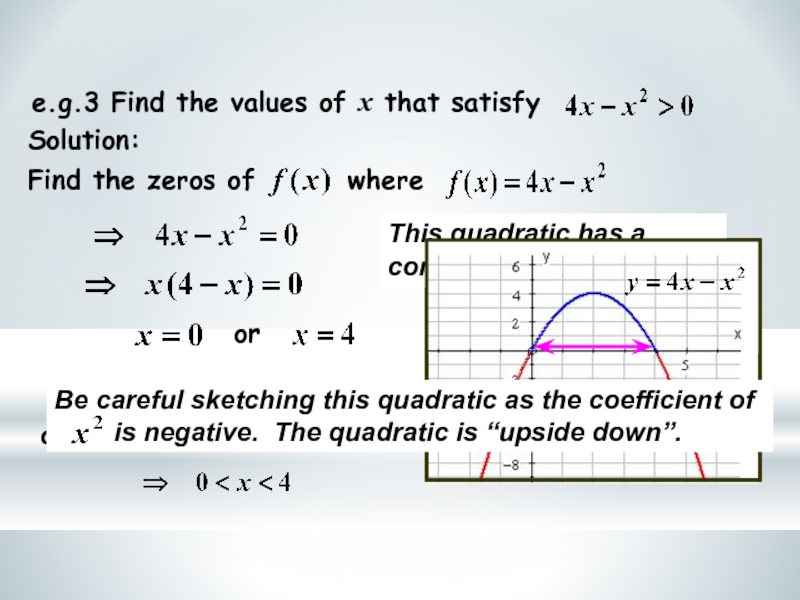
- 8. Solution:e.g.3 Find the values of x that satisfyThis quadratic has a common factor, x
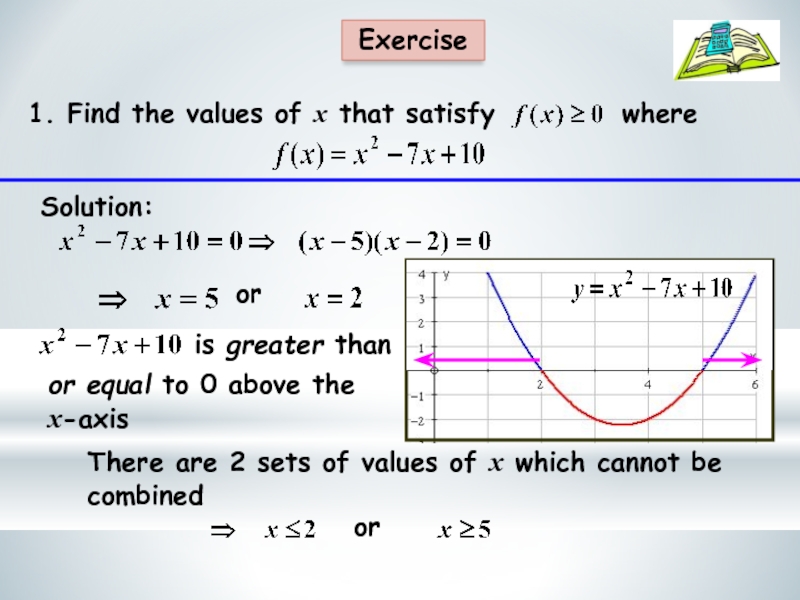
- 9. ExerciseThere are 2 sets of values of x which cannot be combinedSolution:
- 10. Linear inequalitiesSolve as for linear equations BUTKeep
Слайд 2Linear Inequalities
These inequalities can be solved like linear equations EXCEPT that
Consider the numbers 1 and 2 :
Examples of linear inequalities:
Dividing by −1 gives −1 and −2
BUT −1 is greater than −2
−1
−2
1
2
Слайд 3
Linear Inequalities
These inequalities can be solved like linear equations EXCEPT that
Examples of linear inequalities:
Dividing by −1 gives −1 and −2
BUT −1 is greater than −2
The inequality has been reversed
Consider the numbers 1 and 2 :
Слайд 4
Divide by −4:
Solution:
Divide by 3
e.g.2 Find the range of values of
Solution: Collect the like terms
Notice the change from “less than” to “greater than”
Collecting the x-terms on the side which makes the coefficient positive avoids the need to divide by a negative number
Substitute one value of x as a check on the answer
Слайд 5Exercises
Find the range of values of x satisfying the following linear
1.
2.
Solution:
Solution: Either
Or
Divide by -4:
so,
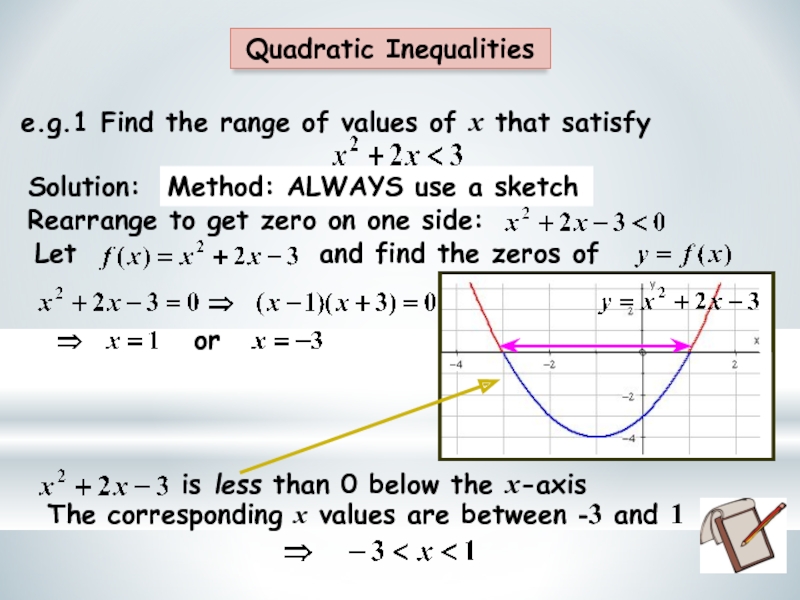
Слайд 6Quadratic Inequalities
Solution:
Rearrange to get zero on one side:
The corresponding x values
Method: ALWAYS use a sketch
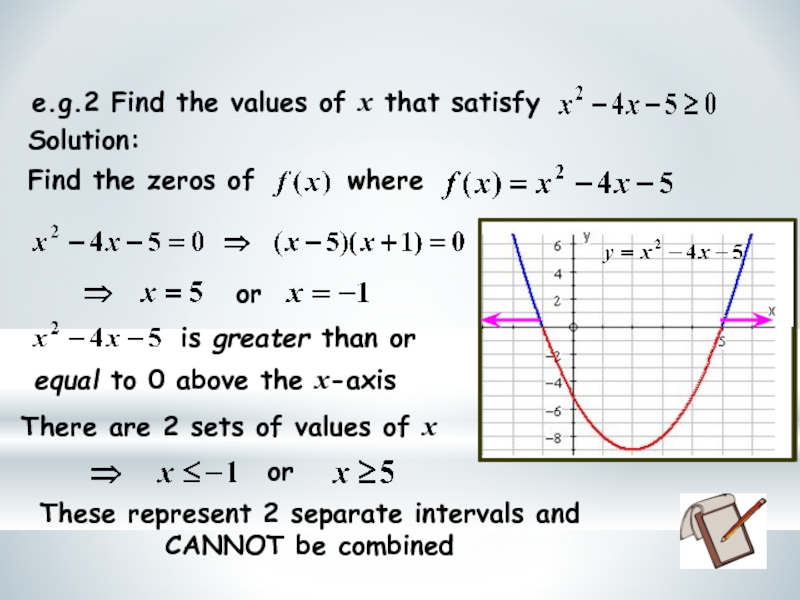
Слайд 7Solution:
There are 2 sets of values of x
These represent 2 separate
Слайд 10Linear inequalities
Solve as for linear equations BUT
Keep the inequality sign throughout
If multiplying or dividing by a negative number, reverse the inequality
Quadratic ( or other ) Inequalities
rearrange to get zero on one side, find the zeros and sketch the function
Use the sketch to find the x-values satisfying the inequality
Don’t attempt to combine inequalities that describe 2 or more separate intervals
SUMMARY