- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Комплексные числа 10-11 класс
Содержание
- 1. Презентация по математике Комплексные числа 10-11 класс
- 2. Человек сначала научился пользоваться натуральными числами, затем
- 3. основные законы сложения и умножениякоммутативный закон
- 4. расширение понятия числа На множестве натуральных чисел
- 5. числовые множества: N – бесконечное упорядоченное, дискретное
- 6. понятие комплексного числаМножество, на котором заданы операции
- 7. ОпределениеКо́мпле́ксные чи́сла (устар. мнимые числа) — числа вида {x+iy}, где {x} и { y} — вещественные числа, {i} — мнимая
- 8. Комплексные числаДля нового множества чисел справедливы основные
- 9. Результаты арифметических операций с комплексными числами совпадают
- 10. Геометрическая интерпретация комплексного числаКомплексное число a +
- 11. Слайд 11
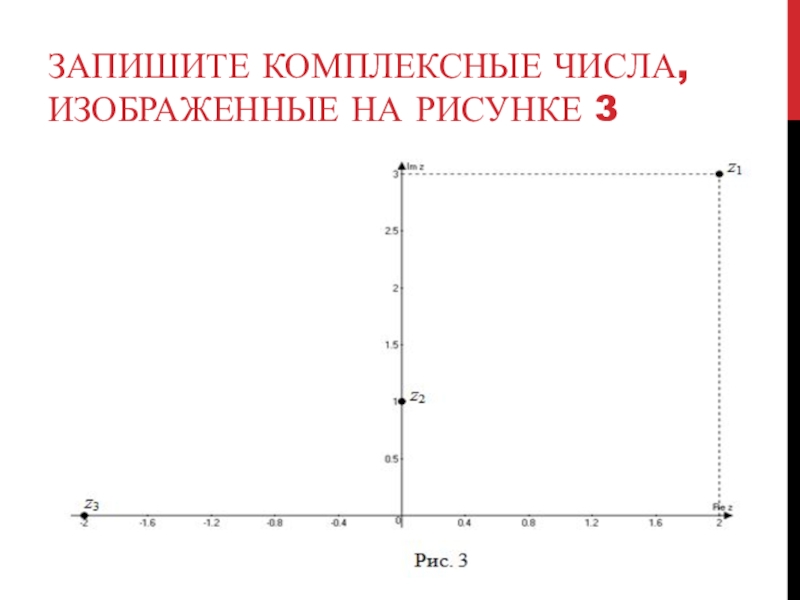
- 12. Запишите комплексные числа, изображенные на рисунке 3
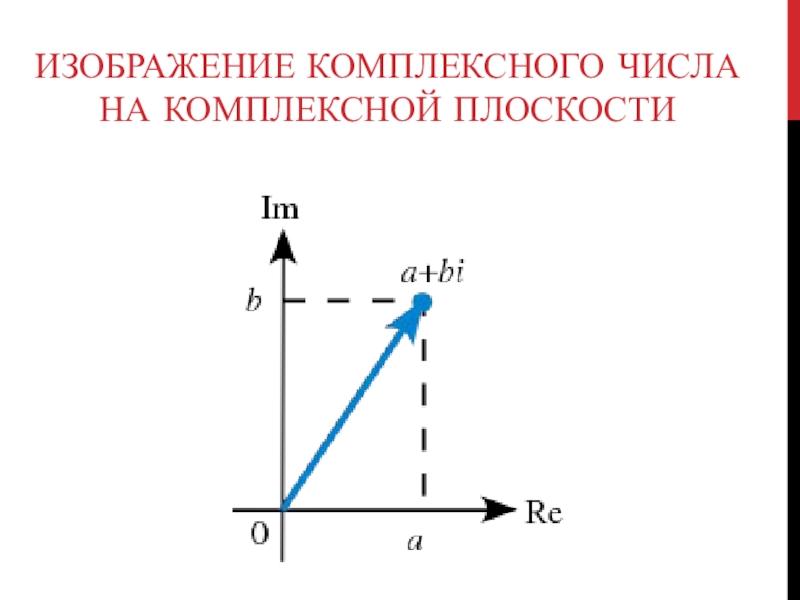
- 13. Изображение комплексного числа на комплексной плоскости
- 14. Комплексно-сопряженные числа
- 15. Свойства комплексно сопряженных чисел
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Алгебраическая форма комплексного числа
- 21. Слайд 21
- 22. Операции с комплексными числами в алгебраической форме
- 23. Сложение комплексных чисел
- 24. Вычитание комплексных чисел
- 25. Умножение комплексных чисел в алгебраической форме
- 26. Деление комплексных чисел в алгебраической форме
- 27. Возведение в степень
- 28. Извлечение корней из комплексных чисел
- 29. Извлечение корня из комплексного числа
- 30. Решить квадратное уравнение
- 31. решитьНайти корни уравнения и разложить квадратный двучлен на множители.
- 32. Практикум по решению задач
Человек сначала научился пользоваться натуральными числами, затем появились рациональные дроби, затем ноль и отрицательные числа и только потом числа иррациональные. Первыми, кто попытался построить законченную теорию вещественного числа, были греки, которые свели рассмотрение чисел к рассмотрению
Слайд 2Человек сначала научился пользоваться натуральными числами, затем появились рациональные дроби, затем
ноль и отрицательные числа и только потом числа иррациональные.
Первыми, кто попытался построить законченную теорию вещественного числа, были греки, которые свели рассмотрение чисел к рассмотрению отрезков прямой, т.е. подошли к изучению числа с точки зрения геометрии.
Современные математики усовершенствовали систему греков.
В основу математической теории может быть положен некоторый абстрактный (идеальный) объект, который не определяется, но формулируются свойства этого объекта или правила действий с этими объектами (эти свойства называются аксиомами).
Используя этот подход можно строго построить теорию натуральных чисел, все остальные числа можно построить на основе натуральных.
«Бог создал натуральные числа, все прочее – дело рук человека» – так сформулировал эту идею немецкий математик Леопольд Кронекер (1823-1891).
Первыми, кто попытался построить законченную теорию вещественного числа, были греки, которые свели рассмотрение чисел к рассмотрению отрезков прямой, т.е. подошли к изучению числа с точки зрения геометрии.
Современные математики усовершенствовали систему греков.
В основу математической теории может быть положен некоторый абстрактный (идеальный) объект, который не определяется, но формулируются свойства этого объекта или правила действий с этими объектами (эти свойства называются аксиомами).
Используя этот подход можно строго построить теорию натуральных чисел, все остальные числа можно построить на основе натуральных.
«Бог создал натуральные числа, все прочее – дело рук человека» – так сформулировал эту идею немецкий математик Леопольд Кронекер (1823-1891).
Слайд 3основные законы
сложения и умножения
коммутативный закон сложения
m + n = n + m . Сумма не меняется от
перестановки её слагаемых.
2) ассоциативный закон сложения;
( m + n ) + k = m + ( n + k ) = m + n + k .
Сумма не зависит от группировки её слагаемых.
3) коммутативный закон умножения;
m · n = n · m .
Произведение не меняется от перестановки его сомножителей.
4) ассоциативный закон умножения;
( m · n ) · k = m · ( n · k ) = m · n · k .
Произведение не зависит от группировки его сомножителей.
5) дистрибутивный закон умножения относительно сложения
( m + n ) · k = m · k + n · k
2) ассоциативный закон сложения;
( m + n ) + k = m + ( n + k ) = m + n + k .
Сумма не зависит от группировки её слагаемых.
3) коммутативный закон умножения;
m · n = n · m .
Произведение не меняется от перестановки его сомножителей.
4) ассоциативный закон умножения;
( m · n ) · k = m · ( n · k ) = m · n · k .
Произведение не зависит от группировки его сомножителей.
5) дистрибутивный закон умножения относительно сложения
( m + n ) · k = m · k + n · k
Слайд 4расширение понятия числа
На множестве натуральных чисел мы всегда можем производить
действия сложения и умножения, но обратные действия возможны не всегда.
После введения нуля и отрицательных чисел, т.е. после расширения множества натуральных чисел до множества целых действие вычитания становится возможным для любых двух чисел.
Аналогично, становится возможным действие деления для любых двух чисел, взятых из множества рациональных (разумеется, при условии, что делитель отличен от нуля).
После введения нуля и отрицательных чисел, т.е. после расширения множества натуральных чисел до множества целых действие вычитания становится возможным для любых двух чисел.
Аналогично, становится возможным действие деления для любых двух чисел, взятых из множества рациональных (разумеется, при условии, что делитель отличен от нуля).
Слайд 5числовые множества:
N – бесконечное упорядоченное, дискретное с начальным элементом и
без конечного элемента. Замкнутое относительно операций сложения и умножения;
Z – бесконечное, упорядоченное, дискретное, без начального и конечного элементов. Замкнутое относительно операций сложения, вычитания, умножения;
Q – бесконечное, упорядоченное, без начального и конечного элементов. Замкнутое относительно операций сложения, вычитания, умножения, деления;
R - бесконечное, упорядоченное, без начального и конечного элементов, непрерывное.
Z – бесконечное, упорядоченное, дискретное, без начального и конечного элементов. Замкнутое относительно операций сложения, вычитания, умножения;
Q – бесконечное, упорядоченное, без начального и конечного элементов. Замкнутое относительно операций сложения, вычитания, умножения, деления;
R - бесконечное, упорядоченное, без начального и конечного элементов, непрерывное.
Слайд 6понятие комплексного числа
Множество, на котором заданы операции сложения и умножения, удовлетворяющие
основным законам 1-5, и выполнимы обратные операции: вычитания и деления (за исключением случая, когда делитель равен нулю) называется полем.
Таким образом, множество рациональных чисел образует простейшее числовое поле. Но на множестве рациональных чисел, за исключением редких случаев, невозможна операция, обратная к операции возведения в степень.
Если ввести иррациональные числа, этот пробел частично ликвидируется. На множестве всех вещественных чисел можно извлекать корни любой степени, но только из неотрицательных чисел. Множество вещественных чисел также образует поле, но для того чтобы операция извлечения корня была возможна всегда, требуется дальнейшее его расширение.
Сделаем это с помощью введения искусственных (идеальных) элементов. Введем понятие комплексного числа.
Таким образом, множество рациональных чисел образует простейшее числовое поле. Но на множестве рациональных чисел, за исключением редких случаев, невозможна операция, обратная к операции возведения в степень.
Если ввести иррациональные числа, этот пробел частично ликвидируется. На множестве всех вещественных чисел можно извлекать корни любой степени, но только из неотрицательных чисел. Множество вещественных чисел также образует поле, но для того чтобы операция извлечения корня была возможна всегда, требуется дальнейшее его расширение.
Сделаем это с помощью введения искусственных (идеальных) элементов. Введем понятие комплексного числа.
Слайд 7Определение
Ко́мпле́ксные чи́сла (устар. мнимые числа) — числа вида {x+iy},
где
{x} и { y} — вещественные числа,
{i} — мнимая единица
(величина, для которой выполняется
равенство: { i^{2}=-1}).
Множество комплексных чисел обычно обозначается символом {C} (от лат. complex — тесно связанный).
Множество комплексных чисел обычно обозначается символом {C} (от лат. complex — тесно связанный).
Слайд 8Комплексные числа
Для нового множества чисел справедливы основные законы 1-5.
При этом
для комплексных чисел определено сравнение только типа равны или не равны.
Сравнение типа больше – меньше для этих чисел невозможно.
Комплексное число будет задано, если заданы его вещественная и мнимая части, т.е. заданы два вещественных числа.
Поэтому в курсе алгебры комплексные числа определяют, как упорядоченные пары вещественных чисел (a, b), на множестве которых определены те же три операции:
сравнение;
сложение;
умножение.
Вопрос для работы он-лайн: образует ли поле a) множество иррациональных чисел; b) множество всех конечных десятичных дробей.
Сравнение типа больше – меньше для этих чисел невозможно.
Комплексное число будет задано, если заданы его вещественная и мнимая части, т.е. заданы два вещественных числа.
Поэтому в курсе алгебры комплексные числа определяют, как упорядоченные пары вещественных чисел (a, b), на множестве которых определены те же три операции:
сравнение;
сложение;
умножение.
Вопрос для работы он-лайн: образует ли поле a) множество иррациональных чисел; b) множество всех конечных десятичных дробей.
Слайд 9Результаты арифметических операций с комплексными числами совпадают с результатами, которые мы
получили бы, действуя с вещественными числами.
Этот факт позволяет отождествлять комплексные числа вида a + 0i с вещественными числами и говорить, что множество вещественных чисел R является подмножеством множества комплексных чисел. Аналогично, числа вида 0 + bi будем называть чисто мнимыми и обозначать bi Символ i будем называть мнимой единицей.
Пользуясь правилом умножения комплексных чисел, получим основное свойство мнимой единицы: i2= −1.
Очевидно, что сложение и вычитание комплексных чисел можно производить как сложение и вычитание двучленов, считая подобными те члены, которые не содержат мнимую единицу, и те, которые ее содержат. Аналогично, правило умножения комплексных чисел получается как результат перемножения двучленов с учетом основного свойства мнимой единицы.
Этот факт позволяет отождествлять комплексные числа вида a + 0i с вещественными числами и говорить, что множество вещественных чисел R является подмножеством множества комплексных чисел. Аналогично, числа вида 0 + bi будем называть чисто мнимыми и обозначать bi Символ i будем называть мнимой единицей.
Пользуясь правилом умножения комплексных чисел, получим основное свойство мнимой единицы: i2= −1.
Очевидно, что сложение и вычитание комплексных чисел можно производить как сложение и вычитание двучленов, считая подобными те члены, которые не содержат мнимую единицу, и те, которые ее содержат. Аналогично, правило умножения комплексных чисел получается как результат перемножения двучленов с учетом основного свойства мнимой единицы.
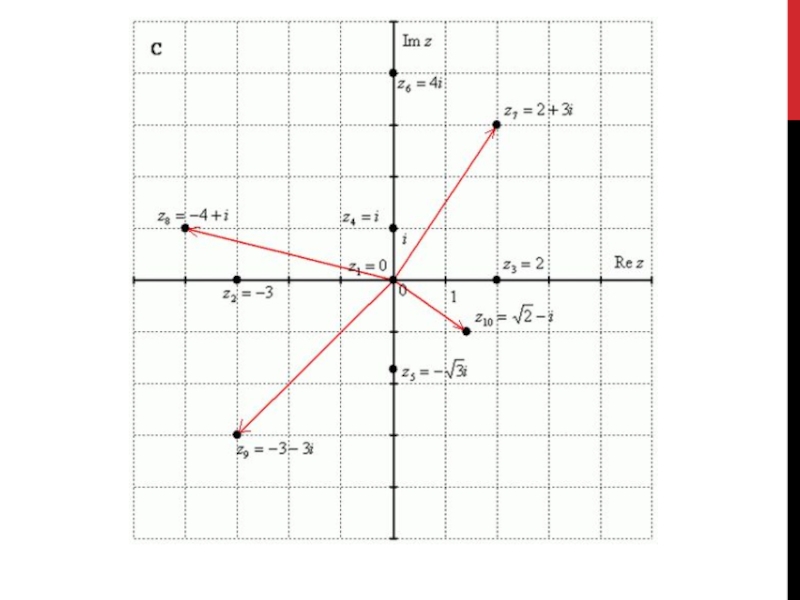
Слайд 10Геометрическая интерпретация комплексного числа
Комплексное число a + bi определяется двумя вещественными
числами, поэтому ему можно сопоставить точку M(a, b) координатной плоскости и, наоборот, каждой точке плоскости M(a, b) можно сопоставить комплексное число a +bi .
Поэтому можно рассматривать комплексные числа как точки плоскости, которую мы будем называть комплексной плоскостью.
Ось абсцисс называют действительной осью, а ось ординат – мнимой.
Поэтому можно рассматривать комплексные числа как точки плоскости, которую мы будем называть комплексной плоскостью.
Ось абсцисс называют действительной осью, а ось ординат – мнимой.