- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Комбинаторика Основные понятия и решение задач
Содержание
- 1. Презентация по математике Комбинаторика Основные понятия и решение задач
- 2. Слайд 2
- 3. Отличительной чертой современного общества является его информативность,
- 4. Прежде, чем приступить к изучению теории вероятностей,Необходимо
- 5. Комбинации, типы комбинацийСоединением (комбинацией) называют объекты или
- 6. ПерестановкиПерестановками из n элементов называются такие соединения,
- 7. Перестановки1. Сколькими способами можно составить список из
- 8. На дверях четырех одинаковых кабинетов надо
- 9. Слайд 9
- 10. Вычислите:а) 7! б) 8! в) 6! – 5!
- 11. Перестановки с повторениямиПусть имеется совокупность из n
- 12. СочетанияПусть имеется совокупность из n элементов. Из
- 13. Свойства сочетанийЗадача. Для дежурства в аудитории из
- 14. СочетанияВычислите: а) б) в) г)
- 15. Сочетания с повторениямиРассмотрим случай, когда сочетание из
- 16. РазмещенияПусть имеется совокупность из n элементов. Из
- 17. РазмещенияВычислите: а) б) в) г)
- 18. Размещения с повторениями
- 19. Урок 20 Комбинаторные задачи и методы их
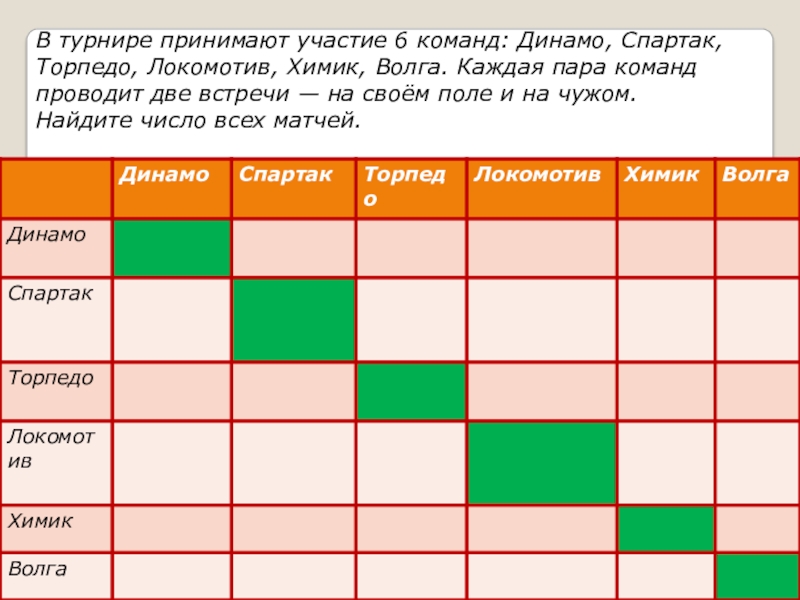
- 20. В турнире принимают участие 6 команд: Динамо,
- 21. В забеге участвует 5 спортсменов. Сколькими способами
- 22. В забеге участвует 5 спортсменов. Сколькими способами
- 23. Замок сейфа открывается. если набрана правильная комбинация
- 24. Замок сейфа открывается. если набрана правильная комбинация
Слайд 3Отличительной чертой современного общества является его информативность, на основе которой можно
Слайд 4Прежде, чем приступить к изучению теории вероятностей,
Необходимо ознакомиться с основными математическими
Основные формулы комбинаторики
Комбинаторика изучает различные группы и
соединения (комбинации).
Слайд 5Комбинации, типы комбинаций
Соединением (комбинацией) называют объекты или предметы объединенные в группу.
Комбинацией
Предметы из которых состоят соединения, называются элементами.
Из элементов одного соединения можно составить другие соединения, которые формируются различными способами.
Слайд 6Перестановки
Перестановками из n элементов называются такие соединения, каждое из которых содержит
Например, возьмем в качестве трех элементов цифры 1, 2, 3, тогда n=3. Построим из них все соединения, которые будут содержать все три элемента и отличаться друг от друга лишь порядком их расположения. Таких соединений будет шесть
( число перестановок из трех элементов).
Число перестановок из n элементов обозначается
(читается: n факториал)
Факториалом называется произведение n натуральных чисел от 1 до n.
Слайд 7Перестановки
1. Сколькими способами можно составить список из пяти фамилий?
Решением задачи является
2. На книжной полке выставлены 8 книг различных авторов.
Сколько способов имеется для расстановки этих книг в различном порядке?
Решением задачи является число перестановок из 8 элементов.
3. Собрание сочинений А.С.Пушкина издано в шести томах.
Сколько существует способов расставить эти тома?
Слайд 8 На дверях четырех одинаковых кабинетов надо повесить таблички с фамилиями
В 10 классе в среду пять уроков: алгебра, геометрия, физкультура, русский язык, английский язык. Сколько можно составить вариантов расписания на этот день?
Адъютант должен развести пять копий приказа генерала пяти полкам. Сколькими способами он может выбрать маршрут доставки копий приказа?
У Вовы на обед – первое, второе, третье блюда и пирожное. Он обязательно начнет с пирожного, а все остальное съест в произвольном порядке. Найдите число возможных вариантов обеда.
Перестановки
Слайд 10Вычислите:
а) 7! б) 8! в) 6! – 5! г)
д)
е)
ж)
з)
Сократите дробь: а)
б)
в)
г)
Решите уравнение: а) n! = 7(n - 1)!
б) (m+17)!=420(m+15)! в) (k – 10)! = 77(k – 11)!
г) (3x)! = 504 (3x -3)!
Перестановки
Слайд 11Перестановки с повторениями
Пусть имеется совокупность из n элементов, среди которых m
Количество возможных перестановок с повторениями из n элементов определяется по формуле:
Задача. Сколько четырехзначных чисел можно составить из двух 1 и двух 2.
Для расчета применим формулу числа перестановок с повторениями.
Задача. Сколькими способами можно переставить буквы в слове ОЛОВО.
Слайд 12Сочетания
Пусть имеется совокупность из n элементов. Из нее выбирают соединения, каждое
сочетаниями из n элементов по m.
Для подсчета числа сочетаний из n элементов по m элементов в каждом, которое обозначается символом будем использовать формулу числа сочетаний:
Слайд 13Свойства сочетаний
Задача. Для дежурства в аудитории из группы студентов 20 человек
Для решения задачи использует общую формулу при n =20, m = 3
Слайд 15Сочетания с повторениями
Рассмотрим случай, когда сочетание из n элементов по m
элементов может содержать любой элемент сколько угодно раз
от 1 до m включительно, или не содержать его совсем.
Такое соединение называется сочетанием с повторениями.
Каждое сочетание с повторениями из n элементов по m
элементов может состоять не только из различных элементов,
но из m каких угодно и как угодно повторяющихся элементов
из числа n или не содержащих их вообще.
Число сочетаний с повторениями можно рассчитать по формуле:
Слайд 16Размещения
Пусть имеется совокупность из n элементов. Из нее выбирают
соединения, каждое
расположения. Такие соединения называются размещениями
из n элементов по m.
Число размещений из n элементов по m элементов в каждом
Обозначается символом и вычисляется по формуле:
Слайд 19Урок 20 Комбинаторные задачи
и методы их решения
УПРАЖНЕНИЯ
В турнире принимают участие
Указание: Для решения задачи Вы можете использовать один из рассмотренных выше способов. Мы рекомендуем составить график встреч.
В забеге участвует 5 спортсменов. Сколькими способами можно предсказать распределение первых трёх мест, считая что победители показывают разное время?
Указание: переберите возможные варианты с помощью дерева.
Замок сейфа открывается. если набрана правильная комбинация из четырёх цифр от 0 до 9. Преступник пытается открыть сейф и набирает шифр наудачу. Найдите наибольшее возможное число безуспешных попыток.
Указание: подсчитайте число способов, с помощью которых можно выполнить каждое действие, состоящее в наборе очередной цифры шифра.
Слайд 20В турнире принимают участие 6 команд: Динамо, Спартак, Торпедо, Локомотив, Химик,
Слайд 21В забеге участвует 5 спортсменов. Сколькими способами можно предсказать распределение первых
Выбор из 5 по 3
Для выбора первого – 5 вариантов
Для выбора второго – 4 варианта
Для выбора третьего – 3 варианта
Всего – 5∙4∙3 = 60
Ответ – 60
Слайд 22В забеге участвует 5 спортсменов. Сколькими способами можно предсказать распределение первых
Выбор из 5 по 3
Для упорядоченной тройки чисел
Число размещений из 5 элементов по 3
Второй способ
Слайд 23Замок сейфа открывается. если набрана правильная комбинация из четырёх цифр от
Выбор из 10 по 4 с повторением
Для выбора первой цифры –10
Для выбора второй – 10 вариантов
Для выбора третьей – 10 вариантов
Для выбора четвертой – 10
Всего – 10∙10∙10∙10 = 10000
Слайд 24Замок сейфа открывается. если набрана правильная комбинация из четырёх цифр от
Выбор из 10 по 4 с повторением
Второй способ