- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике к уроку Применение производной 1 курс СПО
Содержание
- 1. Презентация по математике к уроку Применение производной 1 курс СПО
- 2. Эпиграф урока: ..«Знания иметь отличные, изучая функции различные».
- 3. Лист оценивания студента ____________________
- 4. Устная работа.
- 5. Слайд 5
- 6. Исследование функций с применением производной
- 7. На рисунке изображены график функции у =f(x)
- 8. На рисунке изображены график функции у =f(x)
- 9. Задача 1. На рисунке изображен график функции
- 10. Производная функции в точке х0 равна 0
- 11. Задача 2.На рисунке изображен график функции y
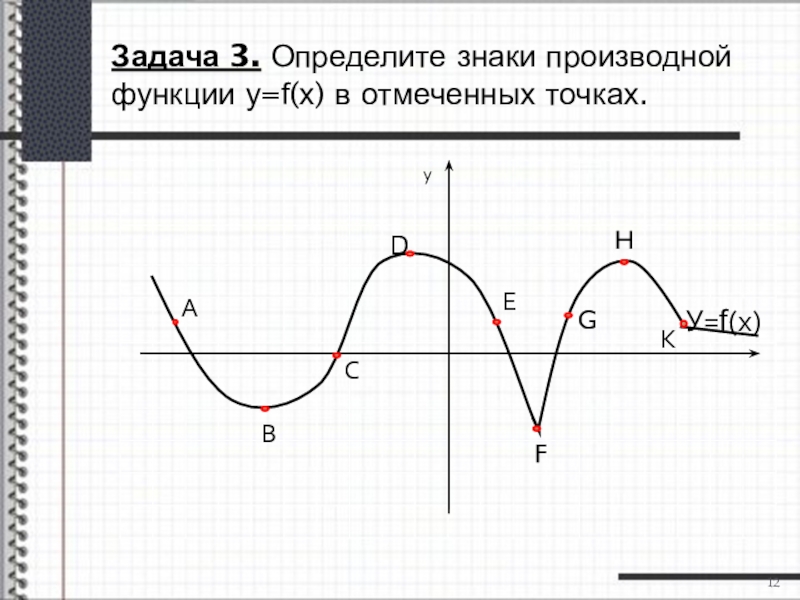
- 12. Задача 3. Определите знаки производной функции у=f(х) в отмеченных точках.0ВАСЕFGHКХ
- 13. Теорема. Если функция у=f(х) имеет экстремум в
- 14. Сравните данный чертеж с предыдущим и подумайте:
- 15. Новые термины:Стационарная точка – внутренняя точка области
- 16. Исследование функции на возрастание (убывание)f(x) дифференцируема на
- 17. Исследование функции на экстремумыПризнак максимума. Если функция
- 18. xyaby=f(x)точка максимуматочка максимуматочкаминимумаf(x)f′(x)ab++--Графическая интерпретация0x
- 19. На рисунке изображён
- 20. Найдите точку минимума функции y = x3
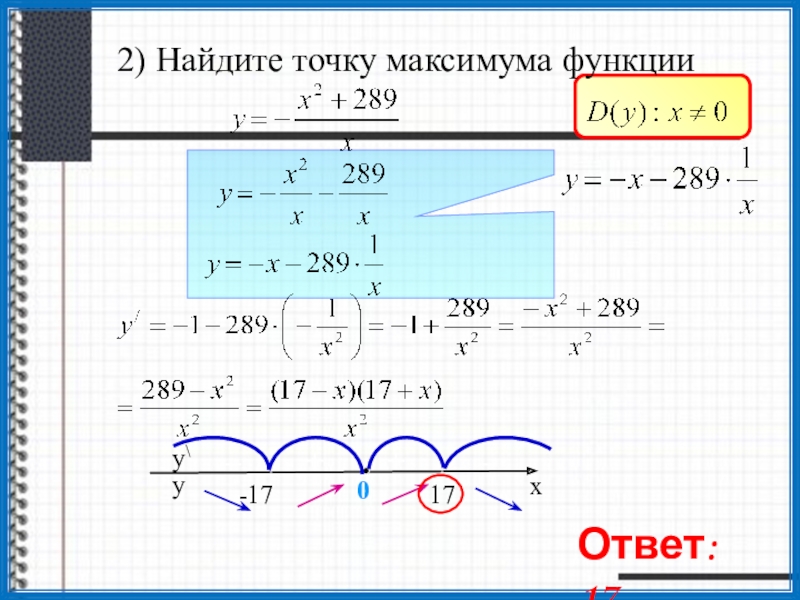
- 21. 2) Найдите точку максимума функции +––+Ответ: 17
- 22. 3) Найдите точку
- 23. 4) Найдите точку минимума функции –+–Ответ: -3
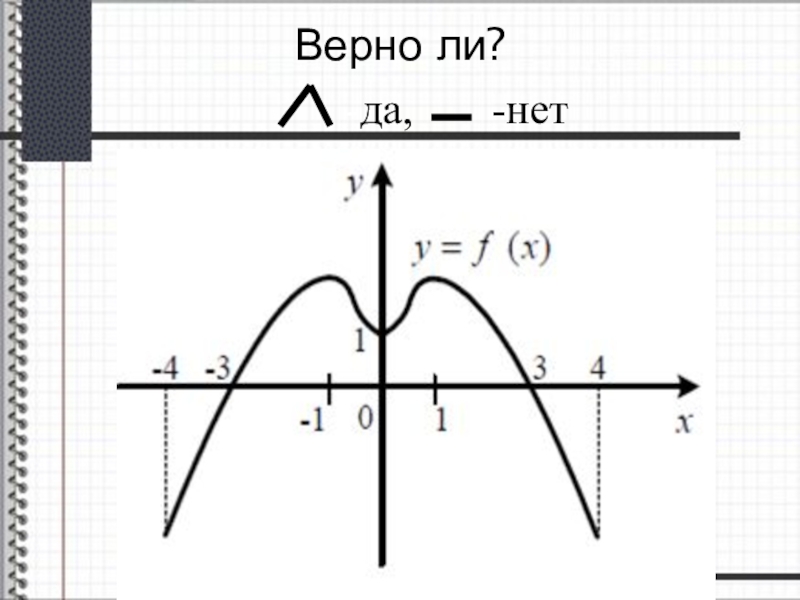
- 24. Верно ли?
- 25. Ответы :1) Функция возрастает на промежутках [x0;x2]
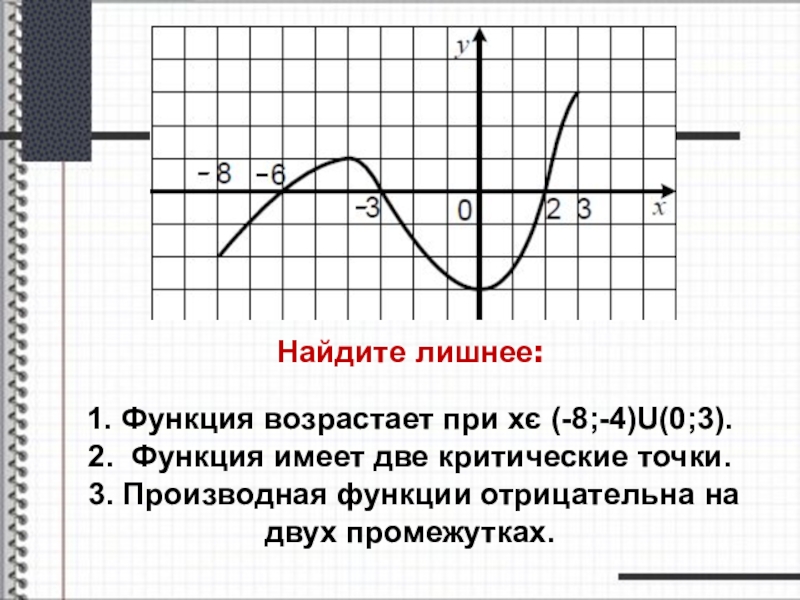
- 26. Найдите лишнее: 1. Функция возрастает при
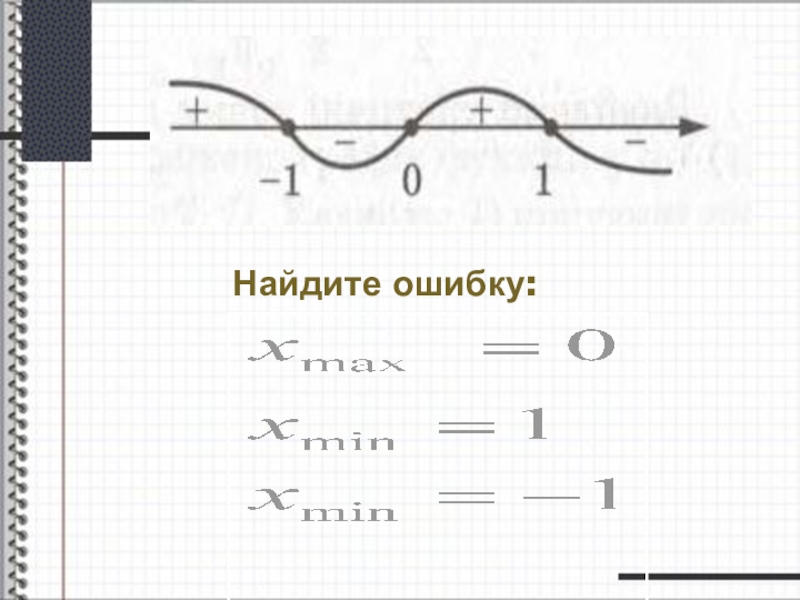
- 27. Найдите ошибку:
- 28. Слайд 28
- 29. Высшее назначение математики - находить порядок в
- 30. Урок принёсРаздражение
- 31. Список литературы и сайтов Виленкин Н.Я.,
- 32. Слайд 32
Слайд 1Автор: Леонтьева Татьяна Юрьевна преподаватель математики ГБОУ
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИИ
Слайд 6
Исследование функций с
применением производной
Исследование функции на экстремумы;
Исследование функции на возрастание/
Исследование функции на наибольшие и наименьшие значения на отрезке;
Исследование функции с помощью графика ее производной (чтение графика производной)
Слайд 7
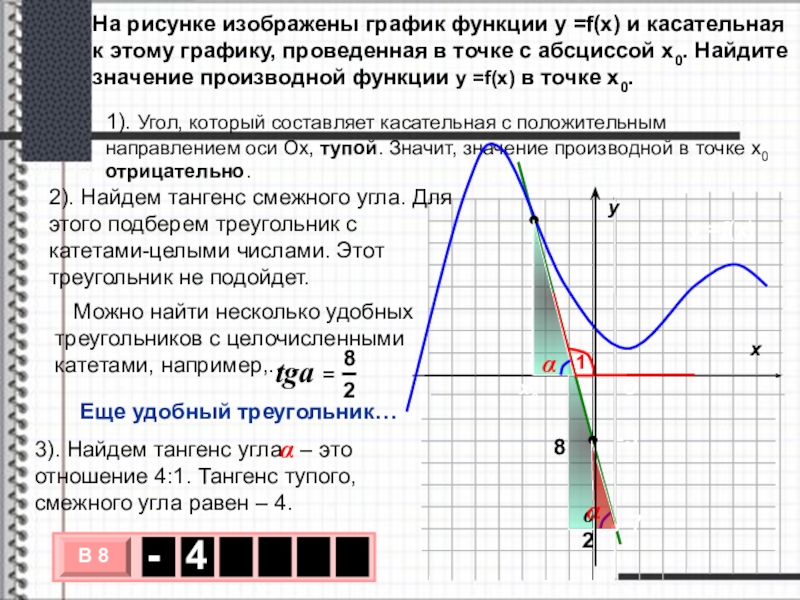
На рисунке изображены график функции у =f(x) и касательная к этому
х
х0
у
1). Угол, который составляет касательная с положительным направлением оси Ох, тупой. Значит, значение производной в точке х0 отрицательно.
2). Найдем тангенс смежного угла. Для этого подберем треугольник с катетами-целыми числами. Этот треугольник не подойдет.
Можно найти несколько удобных треугольников с целочисленными катетами, например,….
O
у =f(x)
-3
-7
Еще удобный треугольник…
Слайд 8
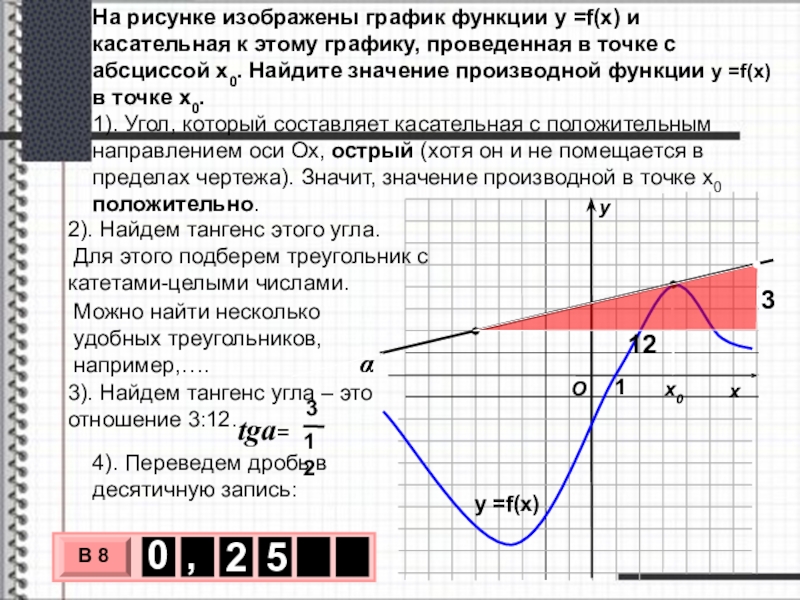
На рисунке изображены график функции у =f(x) и касательная к этому
х
х0
у
O
у =f(x)
1
1). Угол, который составляет касательная с положительным направлением оси Ох, острый (хотя он и не помещается в пределах чертежа). Значит, значение производной в точке х0 положительно.
2). Найдем тангенс этого угла.
Для этого подберем треугольник с катетами-целыми числами.
Можно найти несколько удобных треугольников, например,….
3). Найдем тангенс угла – это отношение 3:12.
α
4). Переведем дробь в десятичную запись:
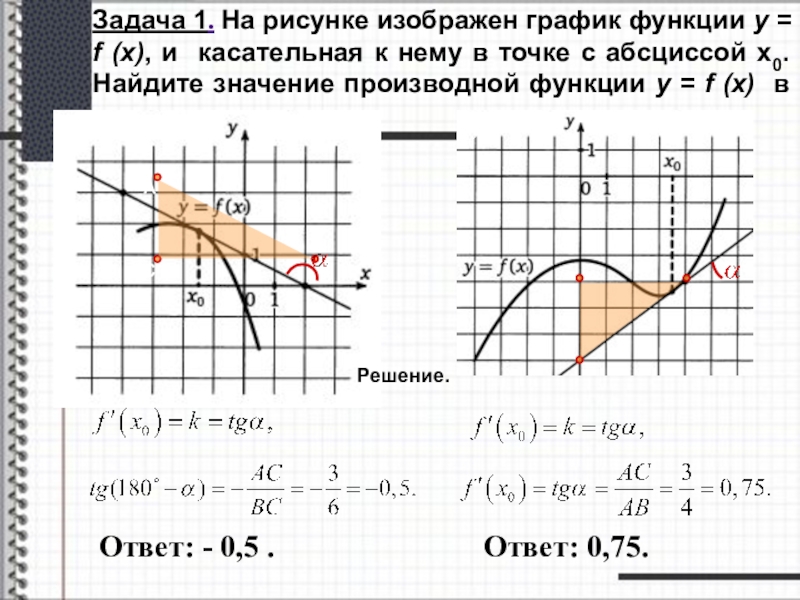
Слайд 9Задача 1. На рисунке изображен график функции y = f (x),
Решение.
Ответ: - 0,5 .
Ответ: 0,75.
С
В
А
a)
б)
Слайд 10Производная функции в точке х0 равна 0 тогда и только тогда,
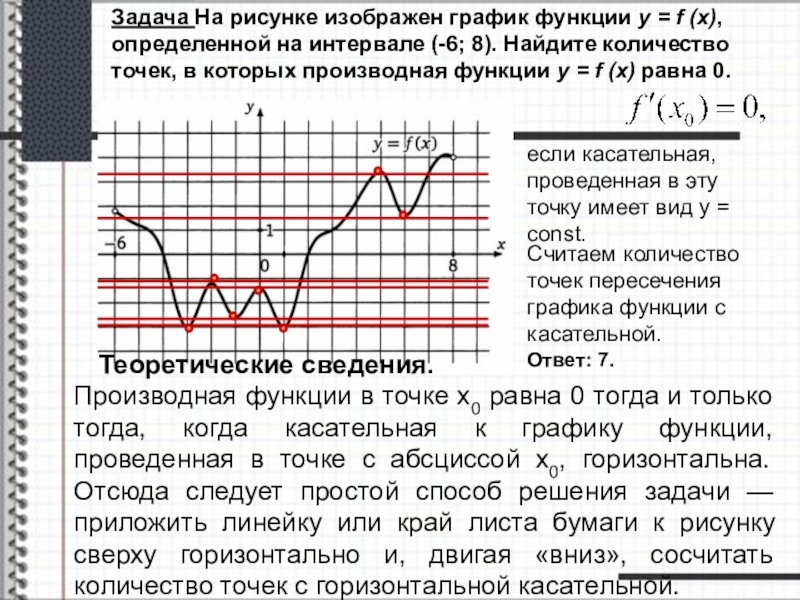
Задача На рисунке изображен график функции y = f (x),
определенной на интервале (-6; 8). Найдите количество точек, в которых производная функции y = f (x) равна 0.
Теоретические сведения.
Решение.
если касательная, проведенная в эту точку имеет вид у = const.
Считаем количество точек пересечения графика функции с касательной.
Ответ: 7.
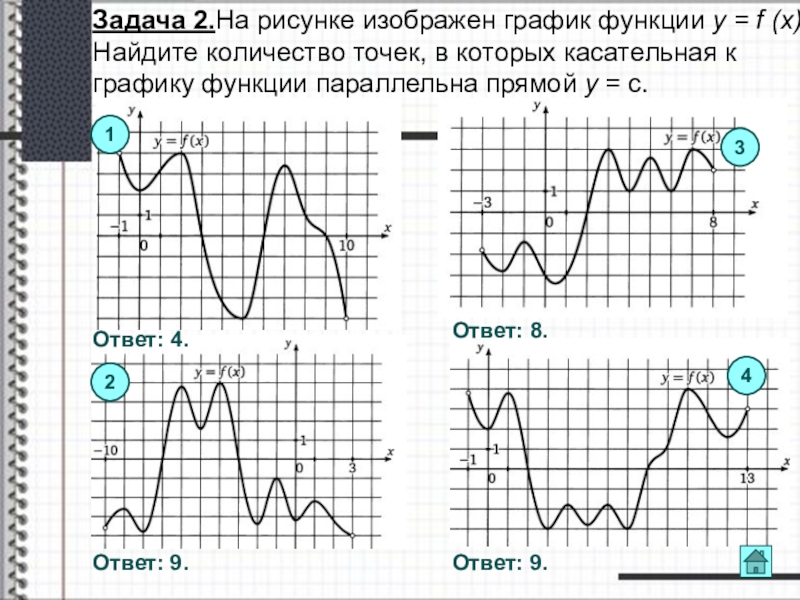
Слайд 11Задача 2.На рисунке изображен график функции y = f (x) Найдите
1
3
4
2
Ответ: 4.
Ответ: 9.
Ответ: 8.
Ответ: 9.
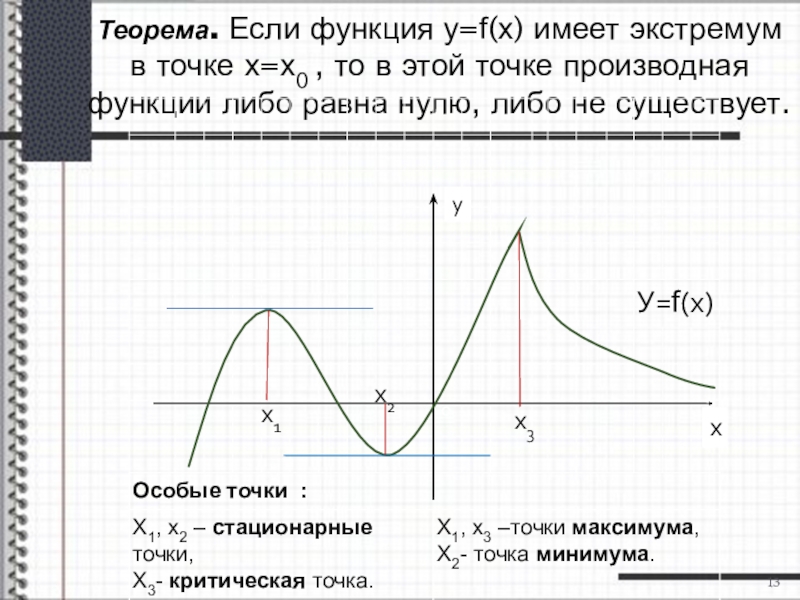
Слайд 13Теорема. Если функция у=f(х) имеет экстремум в точке х=х0 , то
у
х2
х1
х3
х
0
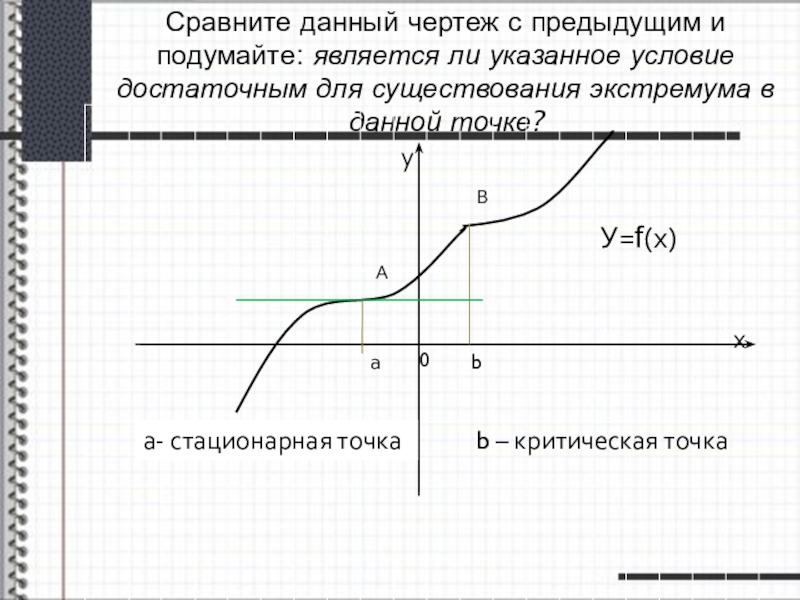
Слайд 14Сравните данный чертеж с предыдущим и подумайте: является ли указанное условие
А
В
а
b
0
а- стационарная точка
b – критическая точка
Слайд 15Новые термины:
Стационарная точка – внутренняя точка области определения функции, в которых
Критическая точка – внутренняя точка области определения функции, в которых функция непрерывна, но производная не существует.
Слайд 16Исследование функции на возрастание (убывание)
f(x) дифференцируема на интервале (a;b)
Если f ′(x)>0
Если f ′(x)<0 в каждой точке интервала, то функция y=f(x) убывает на этом интервале.
Слайд 17Исследование функции на экстремумы
Признак максимума. Если функция f(x) – непрерывна в
Признак максимума. Если функция f(x) – непрерывна в точке х0
Признак минимума. Если функция f(x) – непрерывна в точке х0
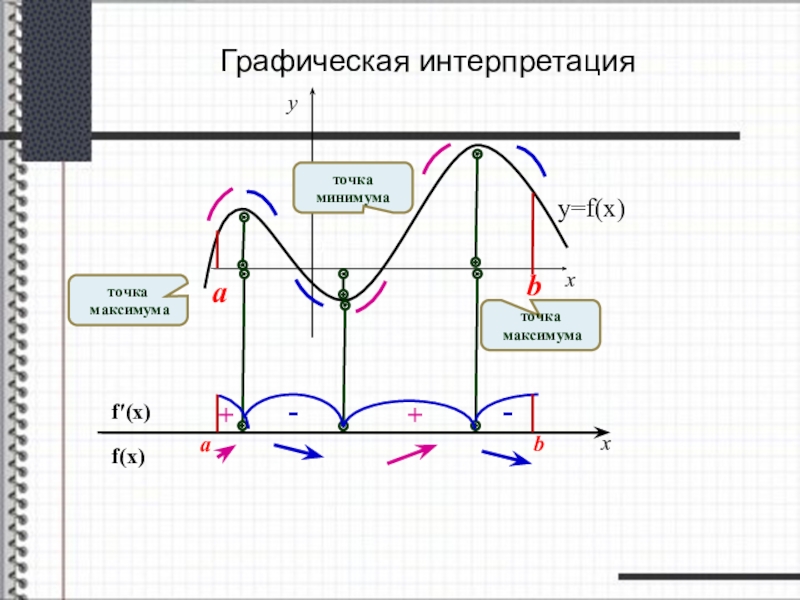
Слайд 18x
y
a
b
y=f(x)
точка
максимума
точка
максимума
точка
минимума
f(x)
f′(x)
a
b
+
+
-
-
Графическая интерпретация
0
x
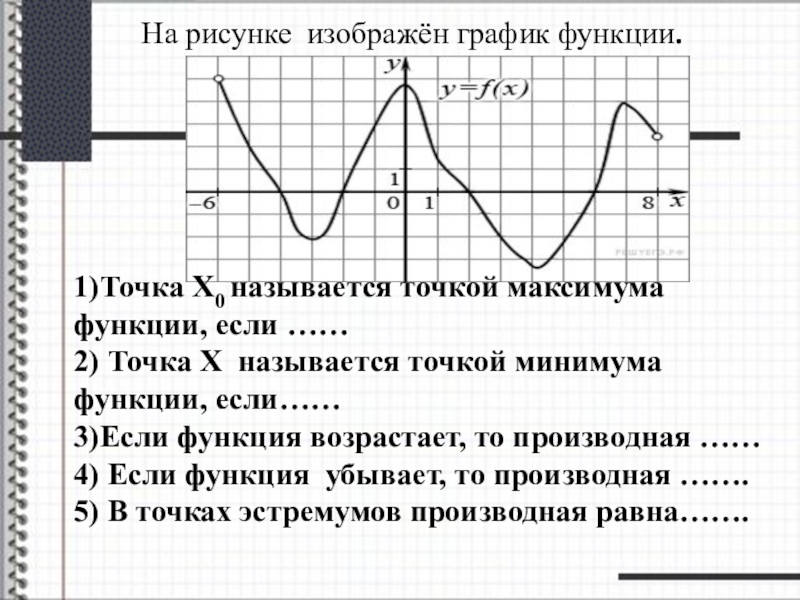
Слайд 19 На рисунке изображён график функции.
1)Точка Х0
2) Точка Х называется точкой минимума функции, если……
3)Если функция возрастает, то производная ……
4) Если функция убывает, то производная …….
5) В точках эстремумов производная равна…….
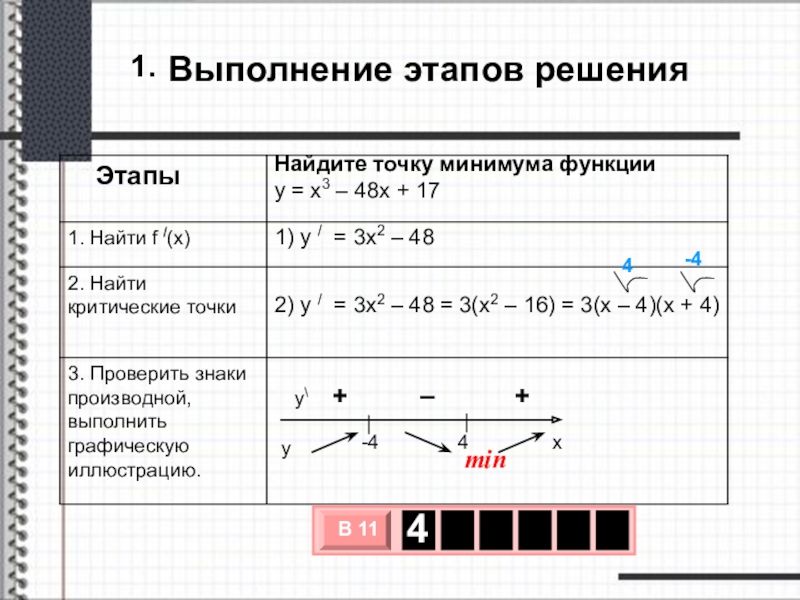
Слайд 20Найдите точку минимума функции
y = x3 – 48x + 17
1)
2) y / = 3x2 – 48 = 3(x2 – 16) = 3(x – 4)(x + 4)
Выполнение этапов решения
min
1.
Слайд 25Ответы :
1) Функция возрастает на промежутках [x0;x2] и [x2;x4]
2) Точки, в
3) Стационарные точки: х0, х2, х4. Критическая точка: х5;
4) Точка минимума- х0, максимума – х4.
Слайд 26Найдите лишнее: 1. Функция возрастает при хє (-8;-4)U(0;3). 2. Функция имеет две критические
Слайд 30Урок принёс
Раздражение Злость
Равнодушие
Радость Наслаждение
Скука Вдохновение
Уверенность Неуверенность
Покой Тревога
Слайд 31
Список литературы и сайтов
Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика, http://www.kodges.ru/34052-kombinatorika.html
Андерсон
М.И. Башмаков «Математика», учебник для учреждений начального и среднего профессионального образования – М. Издательский центр "Академия", 2010 г.
Н.В.Богомолов « Сборник задач по математике» - М.: Дрофа, 2008









![Презентация по математике к уроку Применение производной 1 курс СПО Ответы :1) Функция возрастает на промежутках [x0;x2] и [x2;x4]2) Точки, в Ответы :1) Функция возрастает на промежутках [x0;x2] и [x2;x4]2) Точки, в которых касательная к графику функции у=f(х)](/img/thumbs/3bf3a3336da7dede96deb57a1f4d8a2a-800x.jpg)