- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Геометрический смысл производной. Уравнение касательной и нормали к графику функции.
Содержание
- 1. Презентация по математике Геометрический смысл производной. Уравнение касательной и нормали к графику функции.
- 2. Геометрический смысл производной. Уравнение касательной и нормали к графику функции.
- 3. «Был этот мир глубокой тьмой окутан.Да будет
- 4. Давайте вспомним…
- 5. Что такое приращение аргумента и приращение функции??
- 6. Дайте определение производной функции в точке.
- 7. k Что такое угловой коэффициент прямой?
- 8. Какая формула задает уравнение прямой с угловым коэффициентом?y k x Xo yo
- 9. Как связаны угловые коэффициенты двух перпендикулярных прямых?k 1 k 2 ?
- 10. Что такое касательная к окружности?
- 11. Итак, приступим к изучению новой темы.
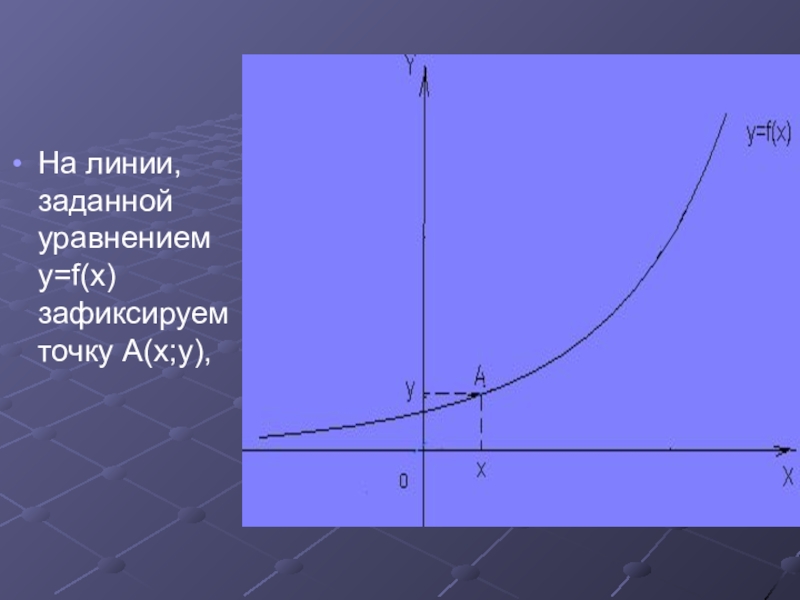
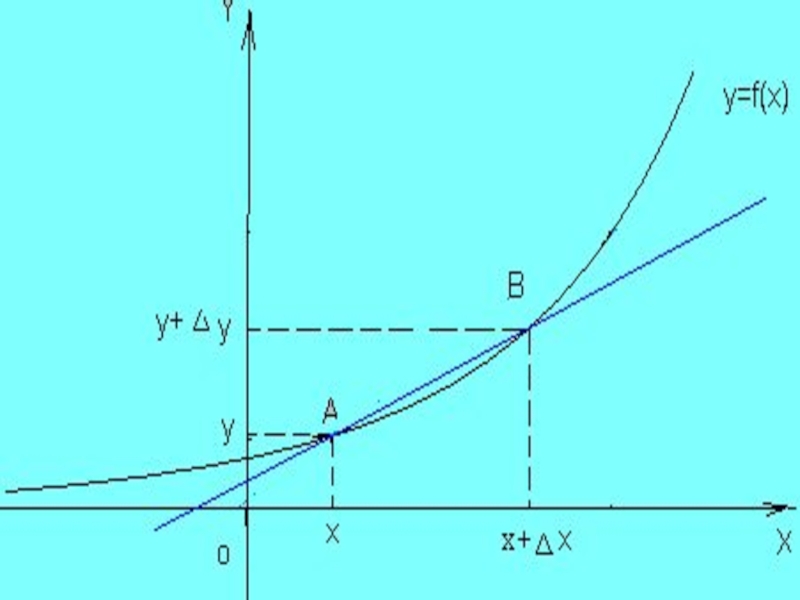
- 12. На линии, заданной уравнением y=f(x) зафиксируем точку A(x;y),
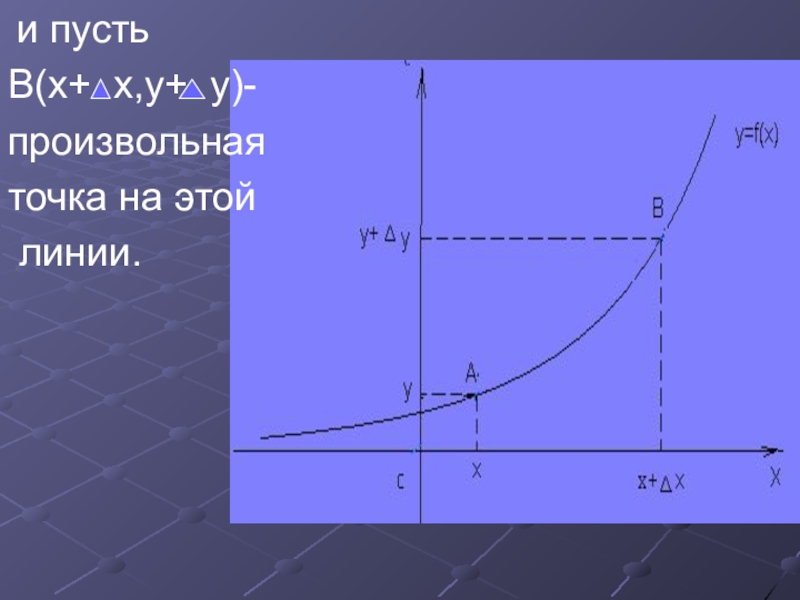
- 13. и пустьB(x+ x,y+ y)-произвольнаяточка на этой линии.
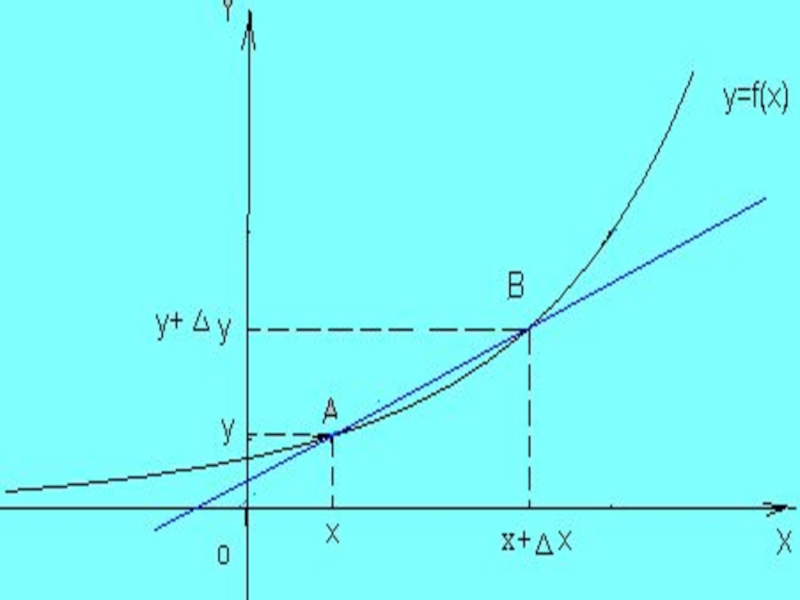
- 14. Проведем секущую AB. - угол наклона секущей AB по отношению к положительному направлению оси Ox.
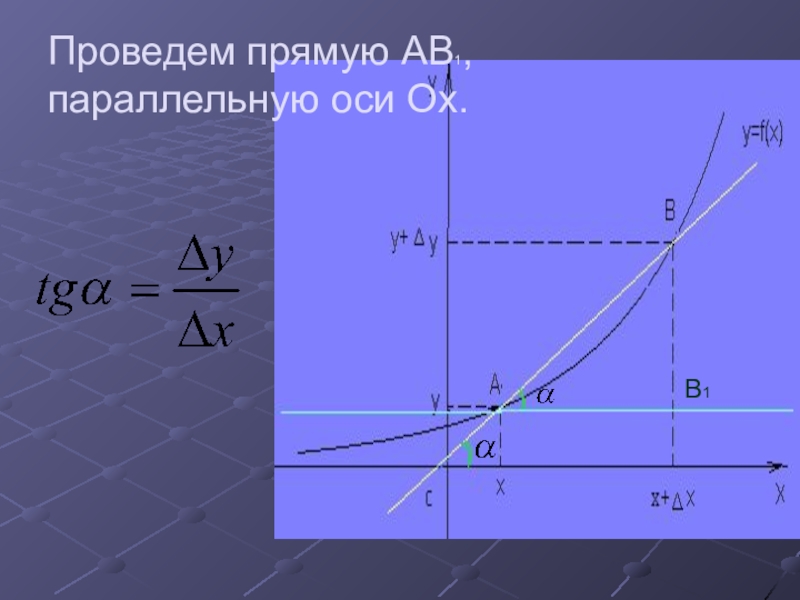
- 15. Проведем прямую AB1, параллельную оси Ox.B1
- 16. Что произойдет с секущей при ?
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
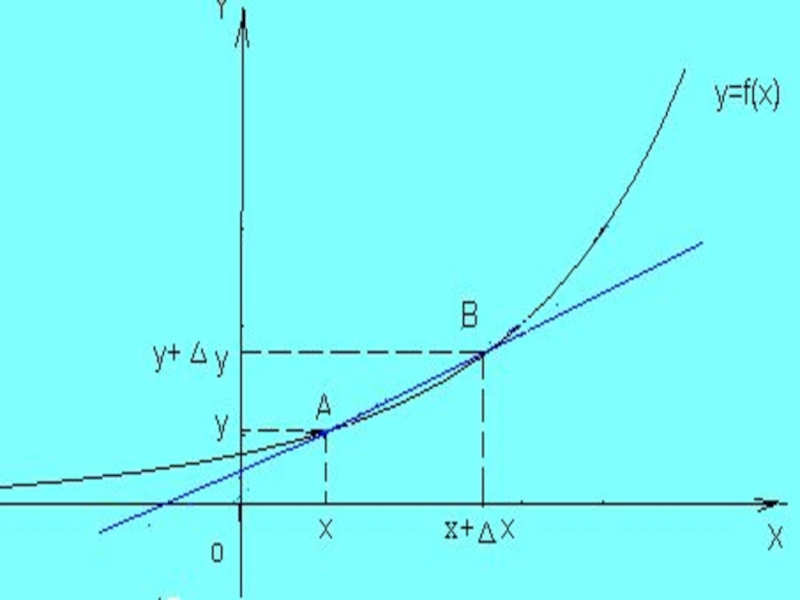
- 23. Таким образом, касательной к линии в данной
- 24. При поэтому
- 25. Обратите внимание!Угол рассматривают между касательной и положительным направлением оси Ох!АВ1-2
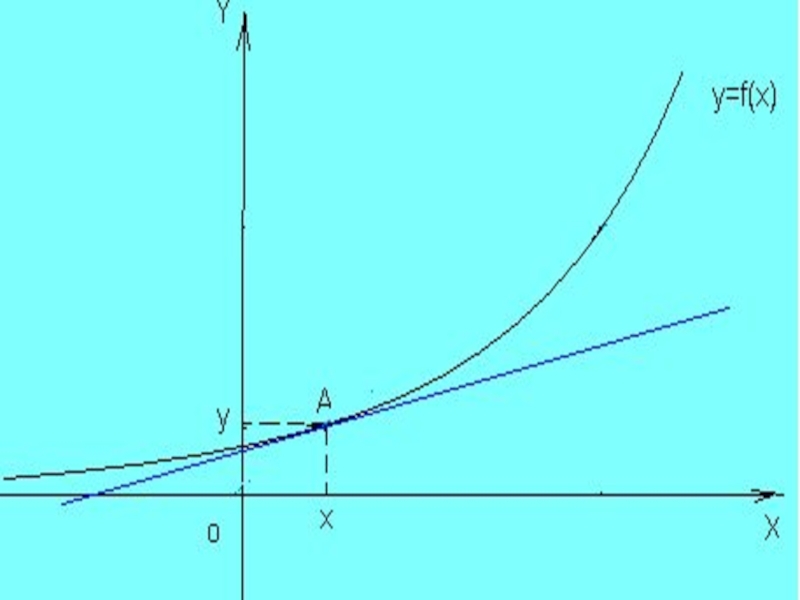
- 26. Геометрический смысл производной функции
- 27. Дифференцирование, или нахождение производной, - это математическая
- 28. Задание1.Найти угловой коэффициент касательной к кривой
- 29. Задание 2.Найти угол наклона касательной к кривой
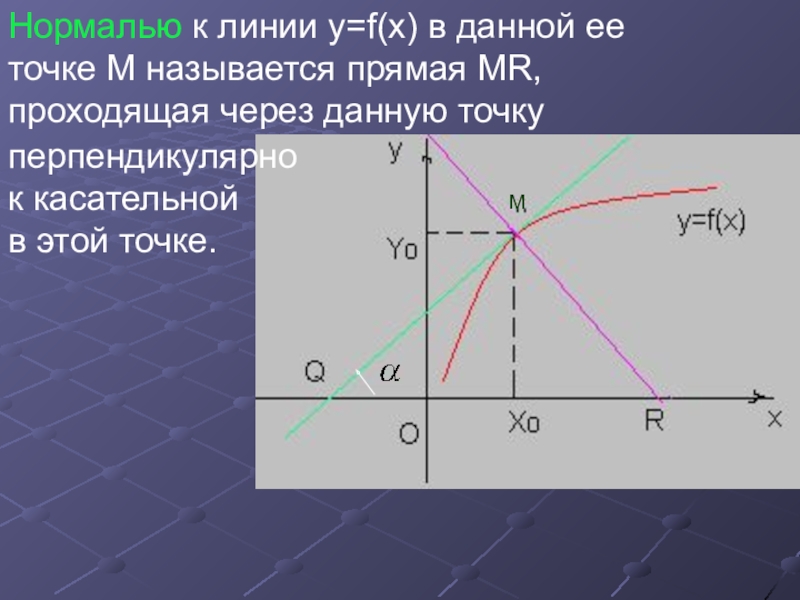
- 30. МНормалью к линии y=f(x) в данной ее
- 31. Так как касательная перпендикулярнанормали, то справедливо равенство:где,-угловой коэффициент касательной, -угловой коэффициент нормали.
- 32. Уравнение касательной к графику функции y=f(x) в
- 33. Задание 3. Известно, что угловой коэффициент касательной
- 34. Задание 4Найдите угловые коэффициенты касательной и нормали
- 35. Задание 5.В какой точке касательная к кривой
- 36. Давайте повторим…Что такое касательная к кривой?Как определить
- 37. Подведем итоги...
- 38. 1.Найдите уравнение касательной к графику функции
Геометрический смысл производной. Уравнение касательной и нормали к графику функции.
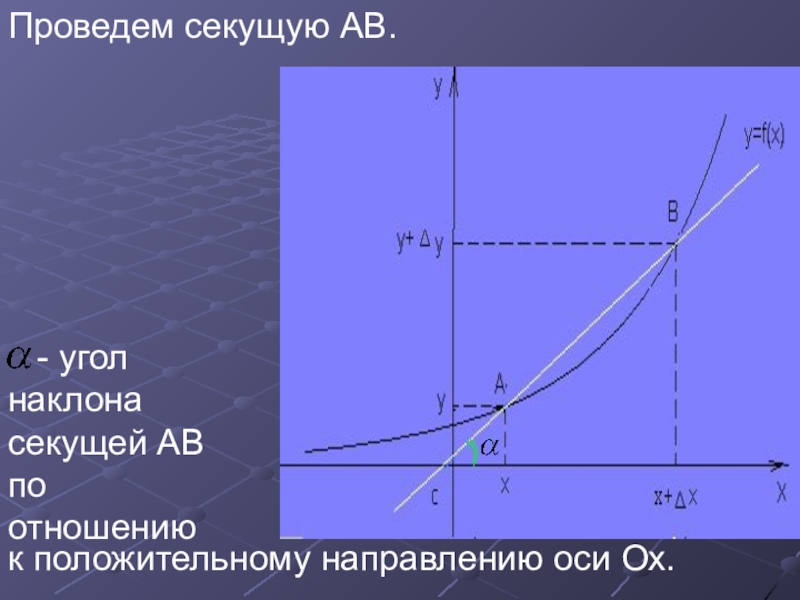
Слайд 14Проведем секущую AB.
- угол наклона секущей AB по отношению
к положительному направлению оси Ox.
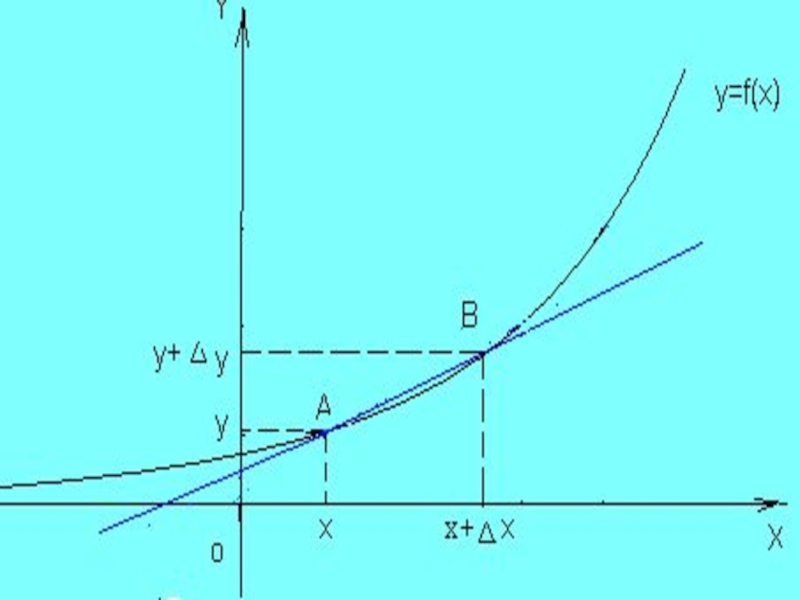
Слайд 23Таким образом, касательной к линии в данной точке А называется предельное
положение секущей АВ при стремлении точки В по линии к точке А.
Слайд 25Обратите внимание!
Угол рассматривают между касательной и положительным направлением оси Ох!
А
В
1
-2
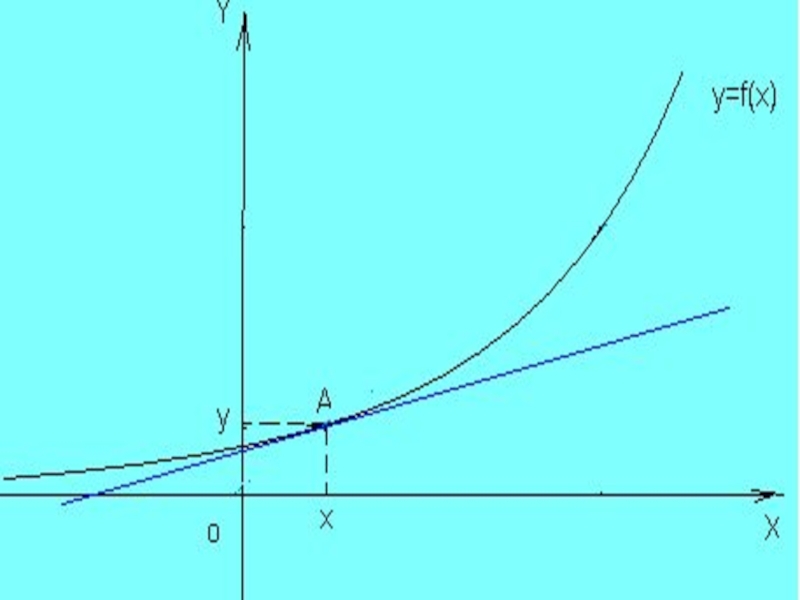
Слайд 26 Геометрический смысл производной функции
состоит в том, что
производная при равна угловому коэффициенту касательной, проведенной к графику данной функции в точке с абсциссой .
производная при равна угловому коэффициенту касательной, проведенной к графику данной функции в точке с абсциссой .
Слайд 27Дифференцирование, или нахождение производной, - это математическая операция, имеющая тот же
смысл, что в механике - нахождение скорости, а в геометрии - вычисление углового
коэффициента касательной.
Слайд 30М
Нормалью к линии y=f(x) в данной ее
точке M называется прямая
MR,
проходящая через данную точку
проходящая через данную точку
перпендикулярно
к касательной
в этой точке.
Слайд 31Так как касательная перпендикулярна
нормали, то справедливо равенство:
где
,
-угловой коэффициент касательной,
-угловой коэффициент
нормали.
Слайд 32Уравнение касательной к графику функции y=f(x) в точке (xo,yo) имеет вид:
Уравнение
нормали к графику
функции y=f(x) в точке (xo,yo) имеет
вид:
функции y=f(x) в точке (xo,yo) имеет
вид:
Слайд 33Задание 3.
Известно, что угловой коэффициент касательной в некоторой точке равен
.
Каким должен быть угловой коэффициент нормали, проведенной в этой же точке?
Каким должен быть угловой коэффициент нормали, проведенной в этой же точке?
Слайд 34Задание 4
Найдите угловые коэффициенты касательной и нормали к кривой
в точке . Составьте уравнения касательной и нормали к данной кривой в данной точке.
Слайд 36Давайте повторим…
Что такое касательная к кривой?
Как определить угловой коэффициент
касательной?
Что такое
нормаль?
Запишите уравнение нормали.
Запишите уравнение касательной.
В чем заключается геометрический
смысл производной?
Слайд 381.Найдите уравнение касательной к графику
функции
в точке с абсциссой 2 .
2.Составьте уравнение касательной и нормали к линии , проходящей через точку А(1;-2).
3.В какой точке касательная к кривой
наклонена к оси Ох под углом ?
2.Составьте уравнение касательной и нормали к линии , проходящей через точку А(1;-2).
3.В какой точке касательная к кривой
наклонена к оси Ох под углом ?
Домашнее задание: