Саратовской области»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Функция
Содержание
- 1. Презентация по математике Функция
- 2. Повторение
- 3. Школьная математика – это не
- 4. Начиная с XVII века, одним
- 5. Понятие функцииПонятие функции — важнейшее понятие математики.
- 6. Для каждого значения переменной a можно найти
- 7. Определение функции Пусть М есть некоторое
- 8. При этом x называют независимой
- 9. ОПРЕДЕЛЕНИЕ ФУНКЦИИЗАВИСИМОСТЬ ОДНОЙ ПЕРЕМЕННОЙ ОТ ДРУГОЙ НАЗЫВАЮТ
- 10. Наиболее распространенный способ задания функции является ФОРМУЛА
- 11. Пример функции: y=3x. В
- 12. Функция может быть задана формулой.
- 13. Чтобы указать, что y есть функция
- 14. Пусть функция задана формулой, гдеРезультаты вычислений удобно
- 15. Функция может быть задана и
- 16. Термограф состоит из барабана, вращающегося
- 17. На барабан навертывается соответствующим образом
- 18. Выполните задания: №53(у),54,55,56,57(а,в,д)Домашнее задание: п.1.5, №58,65
- 19. Девиз урокаСлова древнегреческого математика Фалеса:- Что есть
- 20. ОПРЕДЕЛЕНИЕМножество всех точек координатной плоскости, абсциссы которых
- 21. Графиком функции y=f(x) называют множество
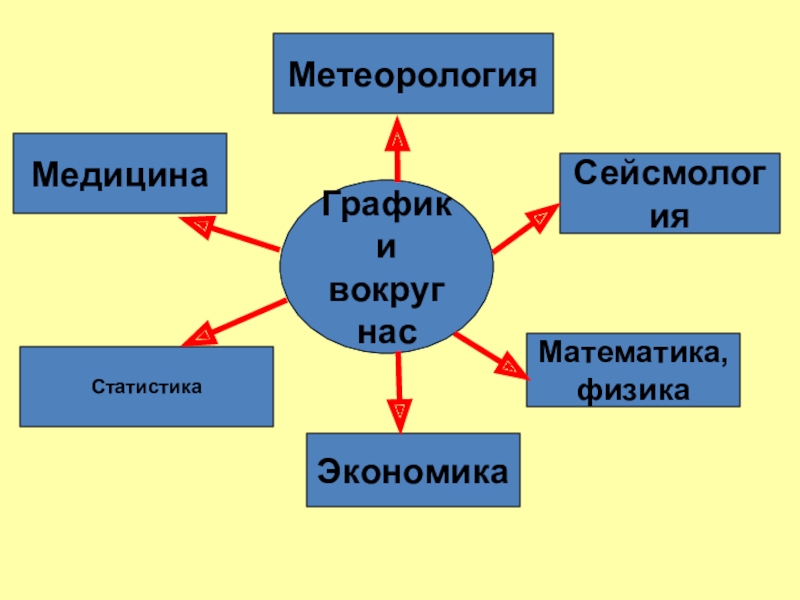
- 22. ГрафикивокругнасМетеорологияСейсмологияСтатистикаЭкономикаМедицинаМатематика,физика
- 23. «Метеорология» Зависимость температуры воздуха от времени
- 24. Зависимость температуры воздуха от времени
- 25. 0134679v, км/чt, ч100График скорости машины v в
- 26. 01346v, км/чt, ч50График скорости машины v в
- 27. 01346v, км/чt, ч50График скорости машины v в
- 28. Медицина. Кардиограмма работы сердца
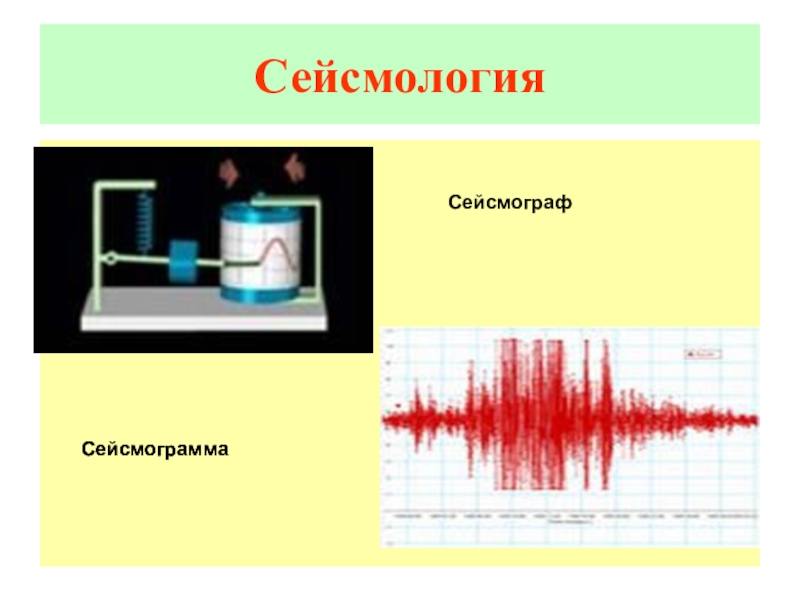
- 29. СейсмологияСейсмограмма Сейсмограмма Сейсмограф
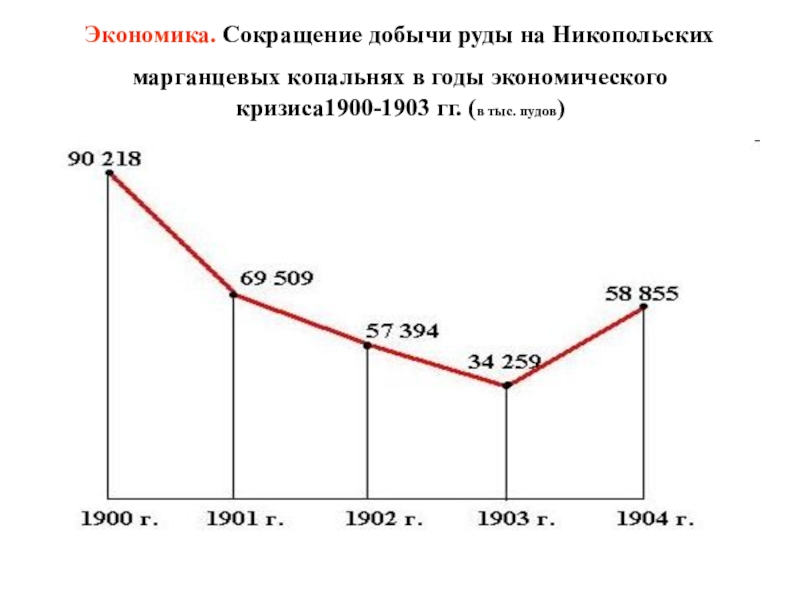
- 30. Экономика. Сокращение добычи руды на Никопольских
- 31. Математика. По графику функции, изображённому на рисунке,
- 32. По графику функции, изображённому на рисунке, найти:1)
- 33. Пусть функция задана формулой, гдеОтметим в координатной
- 34. XY01
Повторение
Слайд 3 Школьная математика – это не наука, а предмет, основная
цель которого – изучение реальных ситуаций с помощью математических моделей математика изучает реальные ситуации, а первичная математическая модель – функция, поэтому функции, их свойства и графики, как в явной, так и в неявной форме составляют стержень школьного курса математики.
Слайд 4 Начиная с XVII века, одним из важнейших понятий является
понятие функции. Оно сыграло и поныне играет большую роль в познании реального мира. Исторический путь развития понятия функции, приходят к мысли о том, что эволюция еще далеко не закончена и, вероятно, никогда не закончится, как никогда не закончится и эволюция математики в целом. Новые открытия и запросы естествознания и других наук приведут к новым расширениям понятия функции и других математических понятий.
Слайд 5Понятие функции
Понятие функции — важнейшее понятие математики. Слово "функция" (от латинского
"Functio" — исполнение обязанностей, деятельность) впервые ввел немецкий ученый Г. Лейбниц.
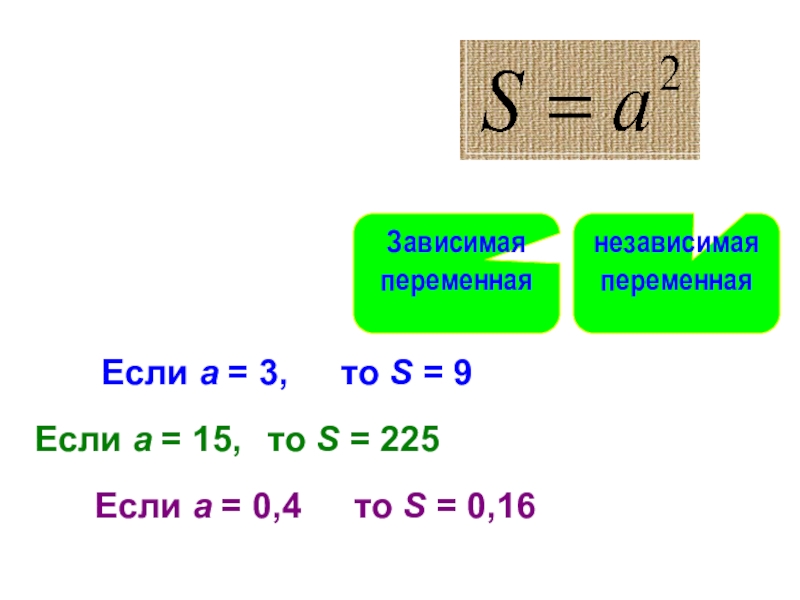
Слайд 6Для каждого значения переменной a можно найти соответствующее значение переменной S
Если
a = 3,
то S = 9
Если a = 15,
Если a = 0,4
то S = 225
то S = 0,16
Зависимая переменная
независимая переменная
Слайд 7Определение функции
Пусть М есть некоторое множество чисел и пусть
каждому числу x из М в силу некоторого (вполне определенного) закона приведено в соответствие (одно) число y, тогда говорят, что y есть функция от x, определенная на множестве М.
Слайд 8 При этом x называют независимой переменной или аргументом, а
y – зависимой переменной или функцией от x, множество М – областью определения функции.
Это определение функции предложено великим русским математиком Н.И.Лобачевским (1792-1856) и немецким математиком П.Дирихле (1805-1859)
Это определение функции предложено великим русским математиком Н.И.Лобачевским (1792-1856) и немецким математиком П.Дирихле (1805-1859)
Слайд 9ОПРЕДЕЛЕНИЕ ФУНКЦИИ
ЗАВИСИМОСТЬ ОДНОЙ ПЕРЕМЕННОЙ ОТ ДРУГОЙ НАЗЫВАЮТ ФУНКЦИОНАЛЬНОЙ ЗАВИСИМОСТЬЮ ИЛИ ФУНКЦИЕЙ.
НЕЗАВИСИСМУЮ
ПЕРЕМЕННУЮ НАЗЫВАЮТ АРГУМЕНТОМ
ЗНАЧЕНИЕ ЗАВИСИМОЙ ПЕРЕМЕННОЙ НАЗЫВАЮТ ЗНАЧЕНИЕМ ФУНКЦИИ
ЗНАЧЕНИЕ ЗАВИСИМОЙ ПЕРЕМЕННОЙ НАЗЫВАЮТ ЗНАЧЕНИЕМ ФУНКЦИИ
Слайд 11 Пример функции: y=3x.
В этом примере закон зависимости
переменной y от переменной x заключается в том, что каждому числу x приводится в соответствие число y, равное 3x. Говорят еще, что функция, выражающая эту зависимость, задана формулой.
Слайд 12 Функция может быть задана формулой. Выше был рассмотрен такой
пример. Функция может быть задана таблицей. Например, если измерять температуру воздуха через каждый час, то каждому моменту времени t=0,1,2,…,24 будет соответствовать определенное число T.
Слайд 13 Чтобы указать, что y есть функция от x, пишут
y= f(x),
где буква f характеризует то правило, по которому получаются значения y, соответствующие данным x. Иногда для того, чтобы подчеркнуть, что y зависит от x, вместо y пишет y= y(x)
где буква f характеризует то правило, по которому получаются значения y, соответствующие данным x. Иногда для того, чтобы подчеркнуть, что y зависит от x, вместо y пишет y= y(x)
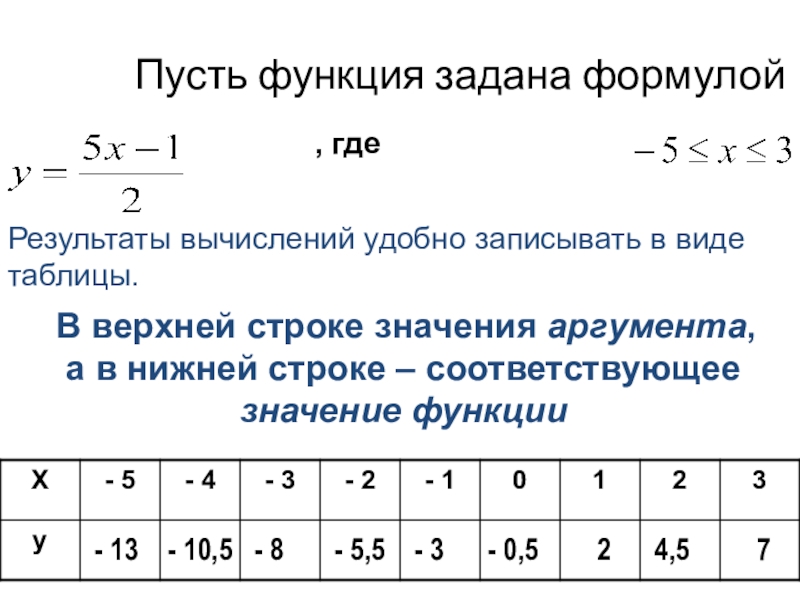
Слайд 14Пусть функция задана формулой
, где
Результаты вычислений удобно записывать в виде таблицы.
В верхней строке значения аргумента,
а в нижней строке – соответствующее значение функции
а в нижней строке – соответствующее значение функции
- 13
- 10,5
- 8
- 5,5
- 3
- 0,5
2
4,5
7
Слайд 15 Функция может быть задана и при помощи графика. Например,
чтобы узнать, как изменяется температура воздуха, на метеорологических станциях пользуются прибором, называемым термографом.
Слайд 16 Термограф состоит из барабана, вращающегося вокруг своей оси при
помощи часового механизма, и латунной прогнутой коробки, чувствительно к изменению температуры. При повышении температуры она разгибается, а прикрепленное к ней при помощи системы рычажков самопишущее перо поднимается вверх. При понижении температуры перо опускается.
Слайд 17 На барабан навертывается соответствующим образом разграфленная бумажная лента, на
которой перо вычерчивает непрерывную линию – график функции, выражающей зависимость между временем и температурой воздуха. При помощи этого графика можно без вычислений определять значения температуры T для каждого момента времени t.
Слайд 19Девиз урока
Слова древнегреческого математика Фалеса:
- Что есть больше всего на свете?
– Пространство.
- Что быстрее всего? – Ум.
-Что мудрее всего? – Время.
- Что приятнее всего?– Достичь желаемого.
- Что быстрее всего? – Ум.
-Что мудрее всего? – Время.
- Что приятнее всего?– Достичь желаемого.
Слайд 20ОПРЕДЕЛЕНИЕ
Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а
ординаты – соответствующим значениям функции называется ГРАФИКОМ ФУНКЦИИ
Слайд 21 Графиком функции y=f(x) называют множество точек координатной плоскости xOy
вида (x;f(x)), где x – любое число из области определения функции.
Если график функции – непрерывная линия, то функцию называют непрерывной.
Если график функции – непрерывная линия, то функцию называют непрерывной.
Слайд 23
«Метеорология»
Зависимость температуры воздуха
от времени суток
0
2
4
6
8
10
12
14
22
24
16
18
20
t, ч
2
4
-2
-6
-4
Т0,С
Переменная t - ?
переменная
Переменная T - ? переменная
Переменная T - ? переменная
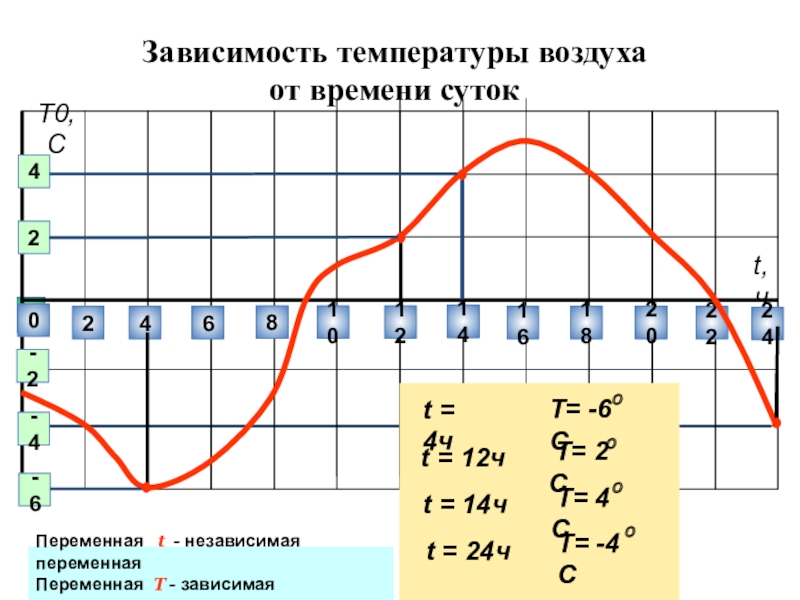
Слайд 24
Зависимость температуры воздуха
от времени суток
0
2
4
6
8
10
12
14
22
24
16
18
20
t, ч
2
4
-2
-6
-4
Т0,С
Переменная t - независимая
переменная
Переменная T - зависимая переменная
Переменная T - зависимая переменная
Слайд 250
1
3
4
6
7
9
v, км/ч
t, ч
100
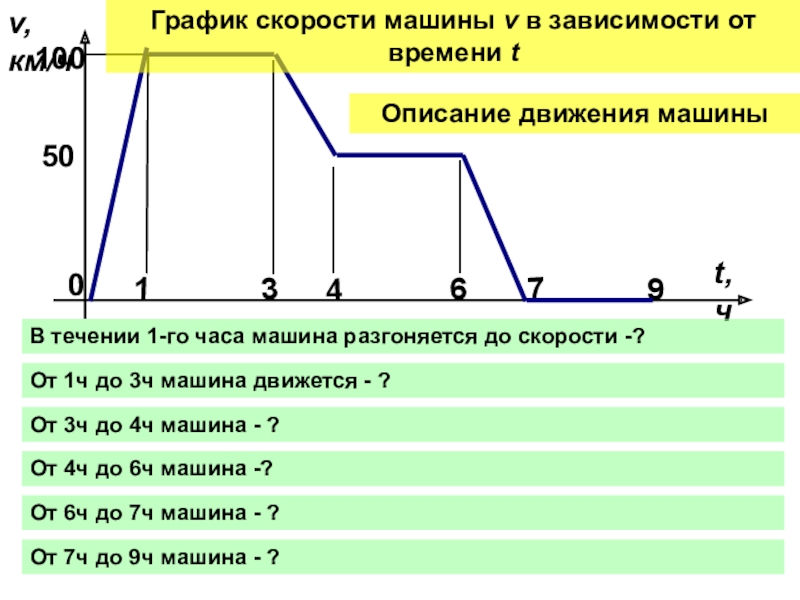
График скорости машины v в зависимости от времени t
Описание
движения машины
В течении 1-го часа машина разгоняется до скорости -?
От 1ч до 3ч машина движется - ?
От 3ч до 4ч машина - ?
От 4ч до 6ч машина -?
От 6ч до 7ч машина - ?
От 7ч до 9ч машина - ?
50
Слайд 260
1
3
4
6
v, км/ч
t, ч
50
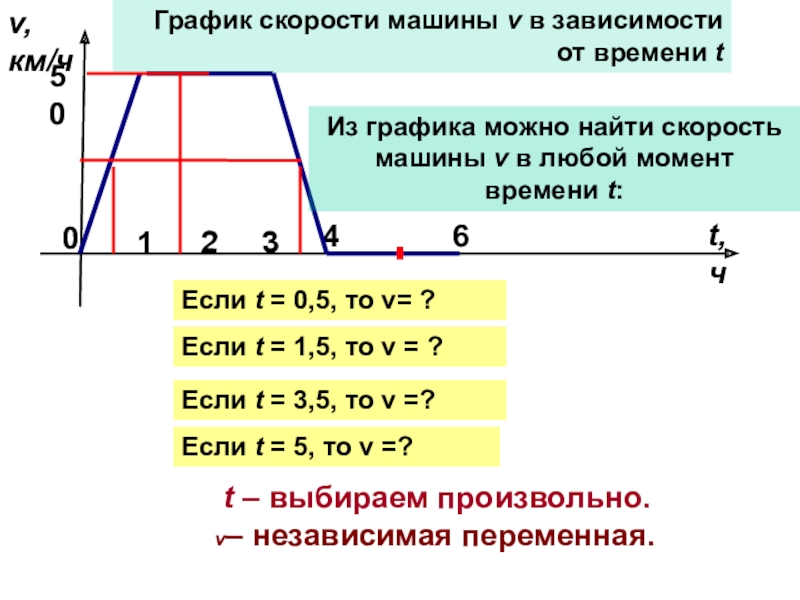
График скорости машины v в зависимости от времени t
Из
графика можно найти скорость
машины v в любой момент времени t:
машины v в любой момент времени t:
Если t = 0,5, то v= ?
Если t = 1,5, то v = ?
Если t = 3,5, то v =?
Если t = 5, то v =?
t – выбираем произвольно.
v– независимая переменная.
2
Слайд 270
1
3
4
6
v, км/ч
t, ч
50
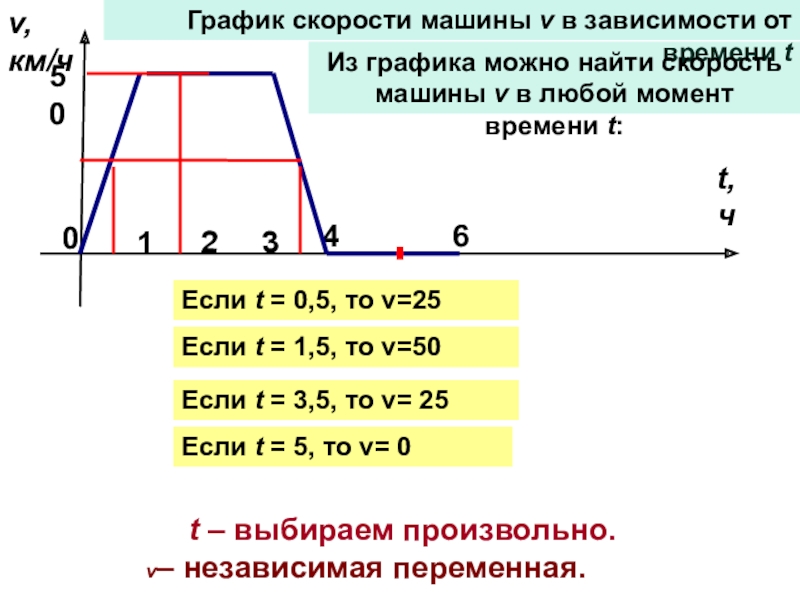
График скорости машины v в зависимости от времени t
Из
графика можно найти скорость
машины v в любой момент времени t:
машины v в любой момент времени t:
Если t = 0,5, то v=25
Если t = 1,5, то v=50
Если t = 3,5, то v= 25
Если t = 5, то v= 0
t – выбираем произвольно.
v– независимая переменная.
2
Слайд 30Экономика. Сокращение добычи руды на Никопольских марганцевых копальнях в годы экономического
кризиса1900-1903 гг. (в тыс. пудов)
Слайд 31
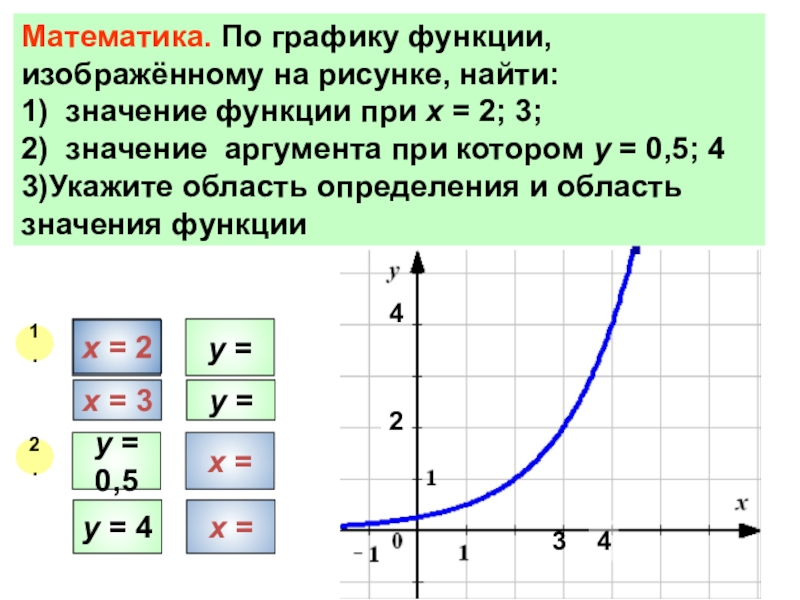
Математика. По графику функции, изображённому на рисунке, найти:
1) значение функции при
х = 2; 3;
2) значение аргумента при котором у = 0,5; 4
3)Укажите область определения и область значения функции
2) значение аргумента при котором у = 0,5; 4
3)Укажите область определения и область значения функции
1.
х = 2
у =
3
2
2.
у = 0,5
4
4
х =
х = 2
х = 3
у =
у = 4
х =
.
Слайд 32
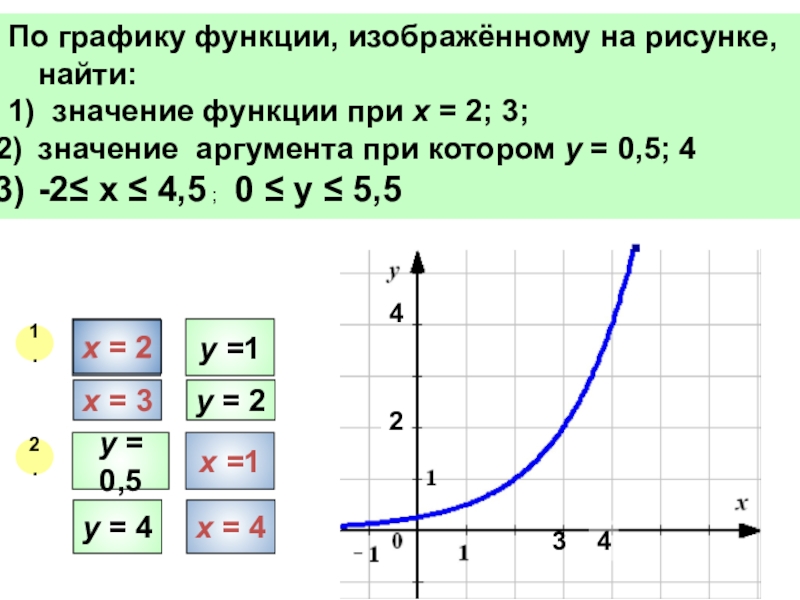
По графику функции, изображённому на рисунке, найти:
1) значение функции при х
= 2; 3;
значение аргумента при котором у = 0,5; 4
-2≤ х ≤ 4,5 ; 0 ≤ у ≤ 5,5
значение аргумента при котором у = 0,5; 4
-2≤ х ≤ 4,5 ; 0 ≤ у ≤ 5,5
1.
х = 2
у =1
3
2
2.
у = 0,5
4
4
х =1
х = 2
х = 3
у = 2
у = 4
х = 4
.
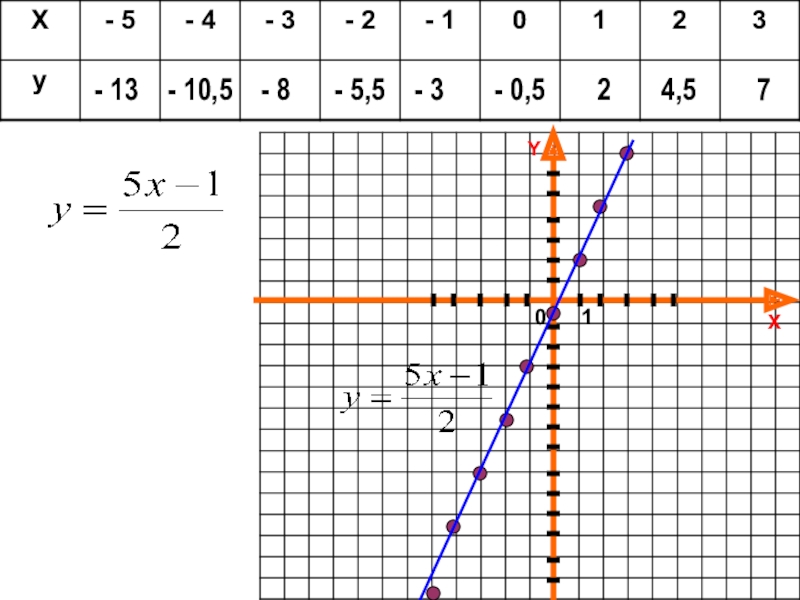
Слайд 33Пусть функция задана формулой
, где
Отметим в координатной плоскости точки, координаты которых
указаны в таблице.
Соединим их плавной линией
