- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике ЕГЭ 11 класс
Содержание
- 1. Презентация по математике ЕГЭ 11 класс
- 2. Слайд 2
- 3. Слайд 3
- 4. В методических материалах дается краткое описание структуры
- 5. Слайд 5
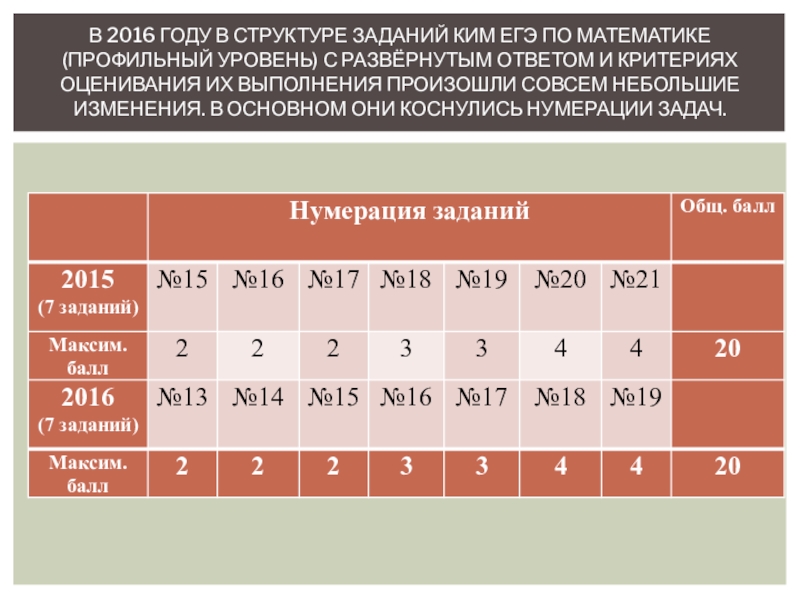
- 6. В 2016 году в структуре заданий КИМ
- 7. ЗАДАНИЕ №13 – уравнение, ЗАДАНИЕ №14 –
- 8. Задания №13 занимают одну из важнейших позиций
- 9. Небольшое уточнение с «неверный ответ» до «неверные
- 10. Возвращаясь к критериям, если: (1) уравнение верно
- 11. Работа не пустая. Она цитирует УММ 2014
- 12. Типичный пример выставления 1 балла по критериям
- 13. Правильные ответы обоснованно получены в пунктах а и б. Оценка эксперта: 2 балла.Комментарий
- 14. Нигде в решении нет описания значений параметра
- 15. КомментарийСтранный случай. В тексте много верных вещей.
- 16. КомментарийПрактически всё верно, только отобранные корни не
- 17. Стереометрическая задача позиционируется как задача для большинства
- 18. Пункт а в заданиях 14 может по
- 19. Возможен и второй вариант, когда в пункте
- 20. Хуже того, вместо честного
- 21. Это отличие не может служить основанием для
- 22. Решения пункта б) нет, а в пункте
- 23. Чертёж верный, но доказательство утверждения пункта а)
- 24. Сечение построено верно и обоснованно получена величина
- 25. Утверждение пункта а не доказано. В пункте
- 26. Всё сделано аккуратно.Оценка эксперта: 2 балла.Комментарий
- 27. Обоснованно получено доказательство утверждения пункта а, хотя
- 28. На этом месте в КИМ 2011–2014 гг
- 29. При переходе к решению одного неравенства поле
- 30. Вот как в точности выглядят критерии оценивания выполнения задания №15.
- 31. При этом в первом случае выставления 1
- 32. Хотя рациональное неравенство «почти» решено, в работе
- 33. Можно отметить верную последовательность всех шагов решения,
- 34. В результате компенсирующих ошибок и частично верных
- 35. Можно отметить не самый удачный путь к
- 36. Вычислительных ошибок в ходе преобразований
- 37. Типичный 1 балл. Путаница в корнях квадратного уравнения, а потом всё верно.Оценка эксперта: 1 балл.Комментарий
- 38. Ответ неверный, все шаги решения присутствуют, но
- 39. ПРЕЗЕНТАЦИЯ СОСТАВЛЕНА ПО МАТЕРИАЛАМ «МЕТОДИЧЕСКИХ РЕКОМЕНДАЦИЙ ПО
Слайд 4В методических материалах дается краткое описание структуры контрольных измерительных материалов 2016
В пособии использованы ответы участников ЕГЭ 2013–2015 гг., а также диагностических и тренировочных работ.
Слайд 6В 2016 году в структуре заданий КИМ ЕГЭ по математике (профильный
Слайд 7ЗАДАНИЕ №13 – уравнение,
ЗАДАНИЕ №14 – стереометрия,
ЗАДАНИЕ №15 –
ЗАДАНИЕ №16 – планиметрия,
ЗАДАНИЕ №17 – текстовая задача экономического содержания,
ЗАДАНИЕ №18 – задание с параметром,
ЗАДАНИЕ №19 – дискретная математика.
Тематическая принадлежность заданий осталась неизменной.
Слайд 8Задания №13 занимают одну из важнейших позиций в структуре КИМ. К их
Критерии проверки и оценка решений заданий 13 (15 в 2015 г., С1 ранее) вариантов КИМ ЕГЭ-2016.
Слайд 9Небольшое уточнение с «неверный ответ» до «неверные ответы» подчеркивает тот факт,
Сохранена такая структура критериев и в 2016 г.
Слайд 10Возвращаясь к критериям, если:
(1) уравнение верно сведено к простейшим тригонометрическим
(2) эти простейшие уравнения не решены или решены с ошибкой;
(3) но при этом отбор корней исходного уравнения верно произведён с помощью тригонометрической окружности, а не по неверно найденным корням простейших тригонометрических уравнений, то по критериям можно выставить 1 балл (получен верный ответ в п. б, а его получение обосновано верным сведением к простейшим уравнениям).
В то же время, при наличии (1) и (2) и «верного» отбора по неверно решенным простейшим уравнениям следует выставлять 0 баллов: любые ошибки, допущенные в тригонометрических формулах, в нахождении значений тригонометрических функций не относятся к вычислительным.
Комментарий. Отбор корней может быть обоснован любым способом: с помощью графика, решения двойных неравенств, ЕДИНИЧНОЙ ОКРУЖНОСТИ и т.п.
Слайд 11
Работа не пустая. Она цитирует УММ 2014 года, где за эту
к
допущена очевидная вычислительная ошибка, а уравнение
решено верно, и затем произведён отбор. К сожалению, в этом отборе есть и описка в 3), есть и ошибка в 1): отобранный корень не принадлежит нужному отрезку.
Оценка эксперта: 0 баллов.
Комментарий
Слайд 12Типичный пример выставления 1 балла по критериям 2014, 2015 гг. При
Оценка эксперта: 1 балл.
Комментарий
Слайд 13Правильные ответы обоснованно получены в пунктах а и б.
Оценка эксперта:
Комментарий
Слайд 14Нигде в решении нет описания значений параметра k, но при отборе
Оценка эксперта: 2 балла.
Комментарий
Слайд 15Комментарий
Странный случай. В тексте много верных вещей. В п. а сначала
Но потом появляется угол в
В результате оба ответа неверны не из-за вычислительной ошибки.
Оценка эксперта: 0 баллов.
(!!!?).
Слайд 16Комментарий
Практически всё верно, только отобранные корни не принадлежат нужному отрезку. Верно
Оценка эксперта: 1 балл.
Слайд 17Стереометрическая задача позиционируется как задача для большинства успевающих учеников, а не
Несколько изменилась структура постановки вопроса. Как и в прошлом году, она разделена на пункты а и б примерно так же, как и задание 13. Соответственно уточнился и общий характер оценивания выполнения решений. Для получения 2 баллов нужно, чтобы выполнялись два условия одновременно (конъюнкция), а для получения 1 балла хватает выполнения хотя бы одного из этих условий (дизъюнкция).
Критерии проверки и оценка решений заданий 14 (16 в 2015 г., С2 ранее) вариантов КИМ ЕГЭ-2016.
Слайд 18Пункт а в заданиях 14 может по разному соотноситься с пунктом
В этой ситуации независимость условий а и б приводит и к независимости проверки их выполнения.
Слайд 19Возможен и второй вариант, когда в пункте а следует доказать утверждение,
Во этой ситуации вполне может встретиться примерно следующий текст.
«Задание 16……
а) Докажите, что…; б) Найдите площадь….
Решение.
У меня а) не получилось. Используем а) при решении б)… далее верное и обоснованное (без выполнения пункта а) вычисление……».
ЗАДАНИЕ 14 (16 в 2015 г. и С2 раннее)
Слайд 20 Хуже того, вместо честного признания о «нерешаемости» а
ЗАДАНИЕ 14 (16 в 2015 г. и С2 раннее)
Слайд 21Это отличие не может служить основанием для снижения оценки. (Кстати, последнее
Отдельно скажем о применении различных формул аналитической геометрии, которыми несколько излишне увлекаются некоторые специалисты. Разумеется, никакого запрета на их использование нет. Однако, если по критериям 2014 года адекватное использование некоторой формулы с допущенной вычислительной ошибкой можно оценить в 1 балл, то условие «обоснованно получен верный ответ в пункте б» критериев 2016 года в таком случае уже не выполнено и (если нет доказательства а) следует выставлять 0 баллов.
Вид ответа может отличаться от приведённого в критериях по проверке заданий с развёрнутым ответом.
Слайд 22Решения пункта б) нет, а в пункте а) нет обоснования того,
Оценка эксперта: 0 баллов.
Комментарий
Слайд 23Чертёж верный, но доказательство утверждения пункта а) отсутствует и пункт б)
Оценка эксперта: 0 баллов.
Комментарий
Слайд 24Сечение построено верно и обоснованно получена величина отношения 5:1. В «Доказать»
Оценка эксперта: 1 балл.
Комментарий
Слайд 25Утверждение пункта а не доказано. В пункте б найдена высота, проведенная
Оценка эксперта: 0 баллов.
Комментарий
Слайд 27Обоснованно получено доказательство утверждения пункта а, хотя нет ссылки на признак
Оценка эксперта: 1 балл.
Комментарий
Слайд 28На этом месте в КИМ 2011–2014 гг была система двух неравенств,
Критерии проверки задания С3 были весьма лаконичны, жестко структурированы, но в то же время и достаточно беспощадны. Вполне грамотный и хорошо подготовленный выпускник, который допускал в решении каждого из неравенств системы хотя бы по одной неточности, получал 0 из возможных 3 баллов, несмотря на все достижения, которые он продемонстрировал в процессе решения. Например, это приводило к тому, что оценка «2 балла» из трёх была более редкой, чем оценка «3 балла» из трёх.
Критерии проверки и оценка решений заданий 15 (18 в 2015 г., С3 ранее) вариантов КИМ ЕГЭ–2016
Слайд 29При переходе к решению одного неравенства поле возможностей при выставлении 0,
Критерии проверки и оценка решений заданий 15 (18 в 2015 г., С3 ранее) вариантов КИМ ЕГЭ–2016
Слайд 31При этом в первом случае выставления 1 балла допускаются только ошибки
Слайд 32Хотя рациональное неравенство «почти» решено, в работе много ошибок. Похоже, автор
Оценка эксперта: 0 баллов.
Комментарий
Слайд 33Можно отметить верную последовательность всех шагов решения, за исключением неравенства с
Оценка эксперта: 0 баллов.
Комментарий
Слайд 34В результате компенсирующих ошибок и частично верных утверждений получена «часть» множества
Оценка эксперта. 0 баллов.
Комментарий
Слайд 35Можно отметить не самый удачный путь к «цели», но способ решения
Оценка эксперта: 2 балла.
Комментарий
Слайд 36 Вычислительных ошибок в ходе преобразований нет. Есть грубая ошибка
Судя по тексту решения, его автор неверно усвоил совет типа «если всё положительно, то от знаменателей можно избавляться крест-накрест»: ведь не просто так написано, что 3/2 > 0.
Оценка эксперта: 0 баллов.
Комментарий
Слайд 37Типичный 1 балл. Путаница в корнях квадратного уравнения, а потом всё
Оценка эксперта: 1 балл.
Комментарий
Слайд 38Ответ неверный, все шаги решения присутствуют, но «случайно» использовалось верное неравенство
Оценка эксперта: 0 баллов.
Комментарий