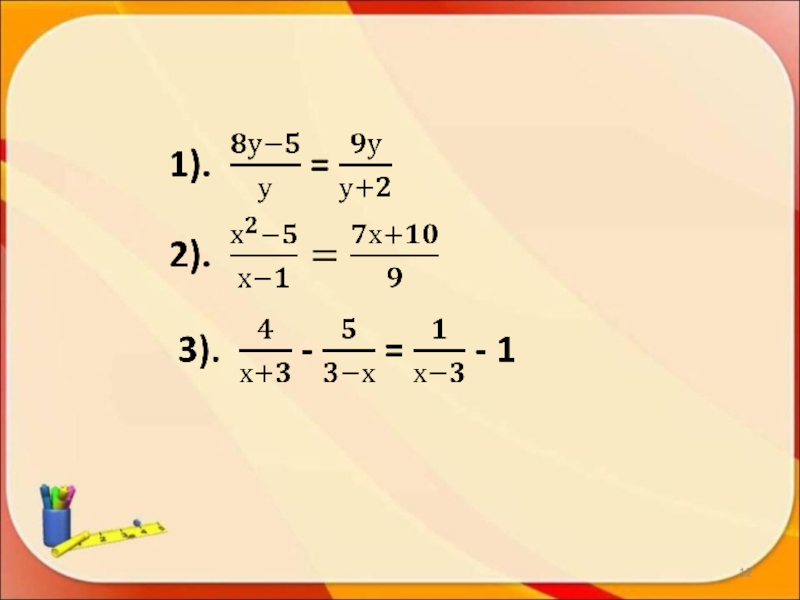уравнения. Определение, область допустимых значений, решение».
8 класс
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Дробно-рациональные уравнения 8 класс
Содержание
- 1. Презентация по математике Дробно-рациональные уравнения 8 класс
- 2. Тема урока: Дробно-рациональные уравнения. Определение, область допустимых
- 3. Литературная гостиная
- 4. Учения об уравнениях есть одна из основных
- 5. Неполные квадратные уравнения и частные виды полных
- 6. Правило решения квадратных уравнений, приведенных к виду
- 7. Французский ученый XVI в. Франсуа Виет первым из математиков
- 8. Впервые квадратное уравнение сумели решить математики Древнего
- 9.
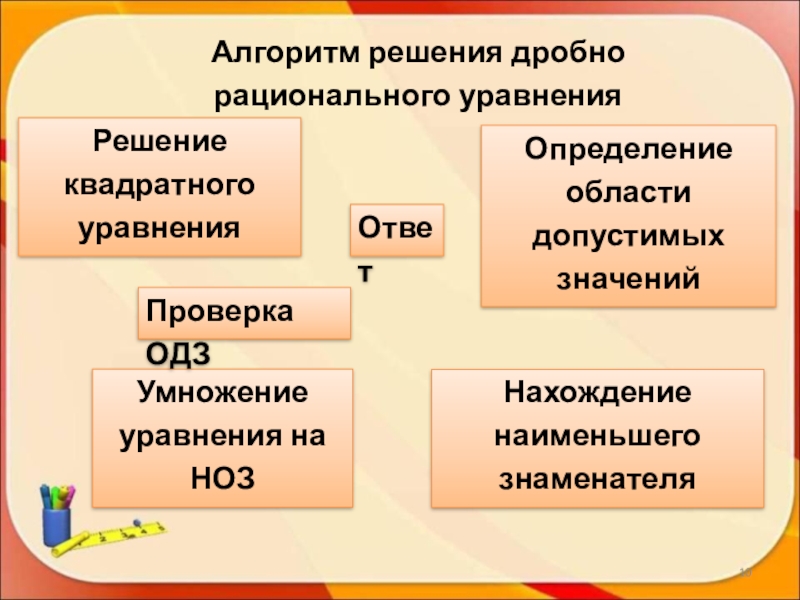
- 10. Алгоритм решения дробно рационального уравненияНахождение наименьшего знаменателяОпределение области допустимых значенийУмножение уравнения на НОЗРешение квадратного уравненияПроверка ОДЗОтвет
- 11. Алгоритм решения дробно рационального уравнения1.Нахождение наименьшего знаменателя2.Определение
- 12.
- 13. № 600(б) № 600(в)№ 601(з) № 602(д)№ 603(г)* № 605(в)Работа в группах
- 14.
- 15.
- 16.
- 17. Задача 1. Две бригады должны были изготовить
- 18.
- 19. 1 группа: 601(е, ж), №603(а-б), №615(а)
- 20. Слайд 20
- 21. Слайд 21
Тема урока: Дробно-рациональные уравнения. Определение, область допустимых значений, решение.Цели урока:1.Совершенствовать навыки решения квадратных уравнений. 2. Познакомиться с дробно- рациональными уравнениями: определение, виды, область определения, решение простейших дробно- рациональных
Слайд 1Учитель математики:
Куликова В.Г.
Общеобразовательная школа І-ІІ ступеней № 26 города Тореза
«Дробно-рациональные
Слайд 2Тема урока: Дробно-рациональные уравнения. Определение, область допустимых значений, решение.
Цели урока:
1.Совершенствовать навыки
решения квадратных уравнений.
2. Познакомиться с дробно- рациональными уравнениями:
определение,
виды,
область определения,
решение простейших дробно- рациональных уравнений.
2. Познакомиться с дробно- рациональными уравнениями:
определение,
виды,
область определения,
решение простейших дробно- рациональных уравнений.
Слайд 4 Учения об уравнениях есть одна из основных тем всей алгебры. С
уравнениями мы сталкиваемся при решении вопросов химии, механики, астрономии.
Решение задач методом составления уравнений является могучим средством при решении многих вопросов производства, строительства и народного хозяйства. Современные вычислительные средства, как микрокалькуляторы, могут вычислять корни уравнения ax²+bx+c=0 по программе, основанной на формулах корней.
Историческая справка
Слайд 5Неполные квадратные уравнения и частные виды полных квадратных уравнении были известны
в глубокой древности.
Примеры решения уравнений дает Диофант Александрийский, живший в ІІІ-веке.
Примеры решения уравнений дает Диофант Александрийский, живший в ІІІ-веке.
Слайд 6Правило решения квадратных уравнений, приведенных к виду , где a>0, дал индийский
ученый Брахмагупта, живший в VII-веке.
В трактате «Китаб аль джабр Валь – мукабала», хорезмский математик аль-Хорезми разъясняет приемы решения линейных, полных и неполных квадратных уравнений ax²=bx, ax²=c, ax²+c=bx, ax²+bx=c.
Слайд 7Французский ученый XVI в. Франсуа Виет первым из математиков ввел буквенные обозначения для
коэффициентов уравнения и неизвестных величин.
А традицией обозначать неизвестные величины последними буквами латинского алфавита (x, y или z) мы обязаны его соотечественнику – Рене Декарту.
Слайд 8Впервые квадратное уравнение сумели решить математики Древнего Египта. Формулу корней квадратного
уравнения называют формулой Виета
Уравнения являются математическими моделями реальных ситуаций, поэтому решение различных практических задач сводится к решению уравнений.
Слайд 10Алгоритм решения дробно рационального уравнения
Нахождение наименьшего знаменателя
Определение области допустимых значений
Умножение уравнения
на НОЗ
Решение квадратного уравнения
Проверка ОДЗ
Ответ
Слайд 11Алгоритм решения дробно рационального уравнения
1.Нахождение наименьшего знаменателя
2.Определение области допустимых значений
3. Умножение
уравнения на НОЗ
4. Решение квадратного уравнения
5. Проверка ОДЗ
6. Ответ
4. Решение квадратного уравнения
5. Проверка ОДЗ
6. Ответ
Слайд 17Задача 1. Две бригады должны были изготовить по 780 деталей. Первая
изготовляла на 9 деталей больше, вторая. Поэтому она выполнила задание на 6 дней раньше. За сколько дней выполнила задание вторая бригада?
Задача 2. Моторная лодка прошла по течению реки 28 км и сразу же вернулась назад, потратив на весь путь 7 часов. Найдите скорость лодки, если скорость реки 3км\ч
Задача 3. Расстояние в 50 км от Тореза до Харцизска мотоциклист проехал с определенной скоростью, а от Харцизска до Донецка со скоростью на 5км\ч меньшей. Найдите первоначальную скорость мотоциклиста, если расстояние от Тореза до Донецка 80км?
Задача 2. Моторная лодка прошла по течению реки 28 км и сразу же вернулась назад, потратив на весь путь 7 часов. Найдите скорость лодки, если скорость реки 3км\ч
Задача 3. Расстояние в 50 км от Тореза до Харцизска мотоциклист проехал с определенной скоростью, а от Харцизска до Донецка со скоростью на 5км\ч меньшей. Найдите первоначальную скорость мотоциклиста, если расстояние от Тореза до Донецка 80км?
Слайд 191 группа: 601(е, ж), №603(а-б), №615(а) на повторение;
2 группа: №603(д,
е) ,№606(а), №615(а) на повторение.
Домашнее задание
